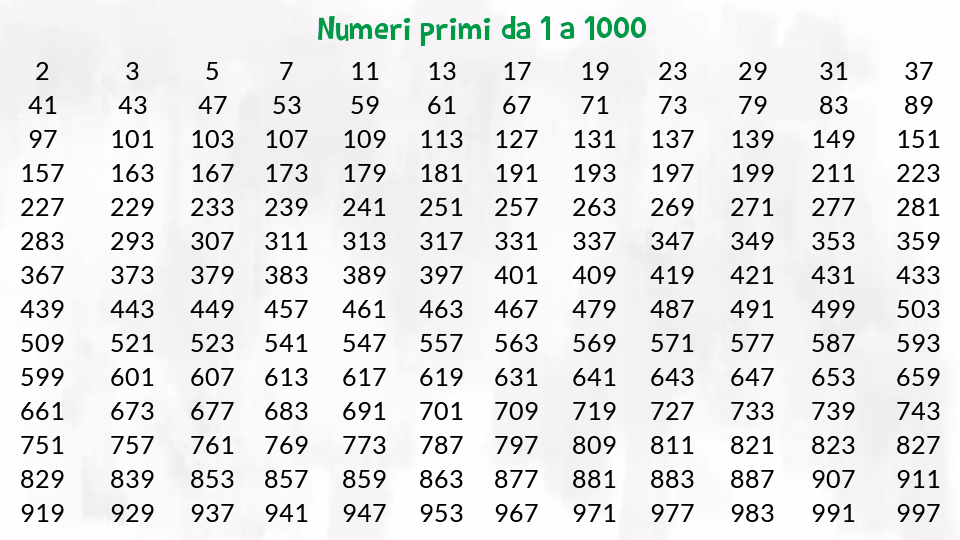
Tutti I Numeri Primi Sono Dispari

I numeri primi rappresentano una pietra angolare della teoria dei numeri, affascinando matematici e studenti per secoli. Un numero primo è definito come un numero intero maggiore di 1 che ha solo due divisori: 1 e se stesso. Esempi comuni includono 2, 3, 5, 7, 11 e così via. Un'affermazione comune, benché imprecisa, è che tutti i numeri primi sono dispari. Analizziamo questa affermazione in dettaglio.
Cosa significa "Tutti i numeri primi sono dispari"?
L'affermazione "Tutti i numeri primi sono dispari" suggerisce che ogni numero primo appartiene all'insieme dei numeri dispari. Un numero dispari è un intero che non è divisibile per 2. Sebbene sia vero che la maggior parte dei numeri primi sono dispari, l'affermazione è errata a causa di una singola eccezione cruciale: il numero 2.
Perché è importante?
L'accuratezza concettuale è fondamentale in matematica. Affermazioni imprecise, anche se apparentemente di poco conto, possono portare a fraintendimenti e errori a cascata durante lo studio di concetti più avanzati. In questo caso specifico, trascurare il numero 2 come numero primo può confondere gli studenti quando imparano a fattorizzare, a calcolare il minimo comune multiplo (MCM) o il massimo comun divisore (MCD), e in altre aree della teoria dei numeri.
Inoltre, questa inesattezza può insinuare un'errata comprensione della logica matematica. Come sottolinea Ian Stewart, "la matematica non è solo calcolo; è ragionamento logico". Un'affermazione universale come "tutti i numeri primi sono dispari" richiede una prova inconfutabile o, in questo caso, viene smentita da un singolo controesempio.
L'impatto sugli studenti
Per gli studenti, questa apparente banalità ha implicazioni significative. Un insegnamento impreciso di base può ostacolare la capacità di applicare correttamente i concetti in problemi più complessi. Ad esempio, uno studente che crede che tutti i numeri primi siano dispari potrebbe erroneamente escludere il 2 durante la fattorizzazione di un numero pari.
Consideriamo un esempio pratico: trovare i fattori primi di 12. Se uno studente crede che tutti i numeri primi siano dispari, potrebbe dimenticare di includere il 2 nella scomposizione, ottenendo una risposta incompleta. La corretta fattorizzazione prima di 12 è 2 x 2 x 3, che evidenzia l'importanza del 2.
Citando Jo Boaler, professoressa di educazione matematica all'Università di Stanford, "gli studenti imparano meglio quando comprendono il 'perché' dietro i concetti, non solo il 'come'". Spiegare perché il 2 è un numero primo e perché costituisce un'eccezione alla regola generale aiuta gli studenti a sviluppare una comprensione più profonda e flessibile dei numeri primi.
Applicazioni pratiche nella scuola e nella vita quotidiana
La comprensione corretta dei numeri primi ha diverse applicazioni pratiche:
- Crittografia: I numeri primi sono fondamentali per gli algoritmi di crittografia moderni che proteggono le nostre comunicazioni online.
- Informatica: I numeri primi vengono utilizzati in tabelle hash e generatori di numeri casuali.
- Vita quotidiana: Anche se non sempre evidenti, i principi dei numeri primi possono aiutare a risolvere problemi di divisibilità e partizione.
In conclusione, mentre la maggior parte dei numeri primi sono dispari, l'affermazione "tutti i numeri primi sono dispari" è falsa. Il numero 2, l'unico numero primo pari, funge da controesempio cruciale. Comprendere questa eccezione è vitale per una solida base in matematica e per evitare potenziali errori in future applicazioni.