Triangolo Rettangolo Circoscritto In Una Circonferenza

Un triangolo rettangolo circoscritto in una circonferenza è un triangolo rettangolo i cui tre vertici giacciono sulla circonferenza stessa. Questa configurazione geometrica speciale presenta proprietà uniche e importanti implicazioni nella geometria euclidea.
Cos'è un Triangolo Rettangolo Circoscritto?
La definizione di triangolo rettangolo circoscritto ruota attorno a due concetti fondamentali: un triangolo rettangolo (avente un angolo di 90 gradi) e una circonferenza. Quando un triangolo rettangolo è "circoscritto" in una circonferenza, significa che tutti e tre i suoi vertici toccano il bordo (la circonferenza) del cerchio. In altre parole, il cerchio passa attraverso tutti i tre vertici del triangolo.
Perché è Importante?
Lo studio dei triangoli rettangoli circoscritti riveste una notevole importanza per diversi motivi, che spaziano dalla teoria alla pratica:
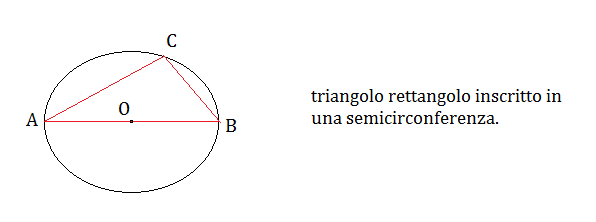
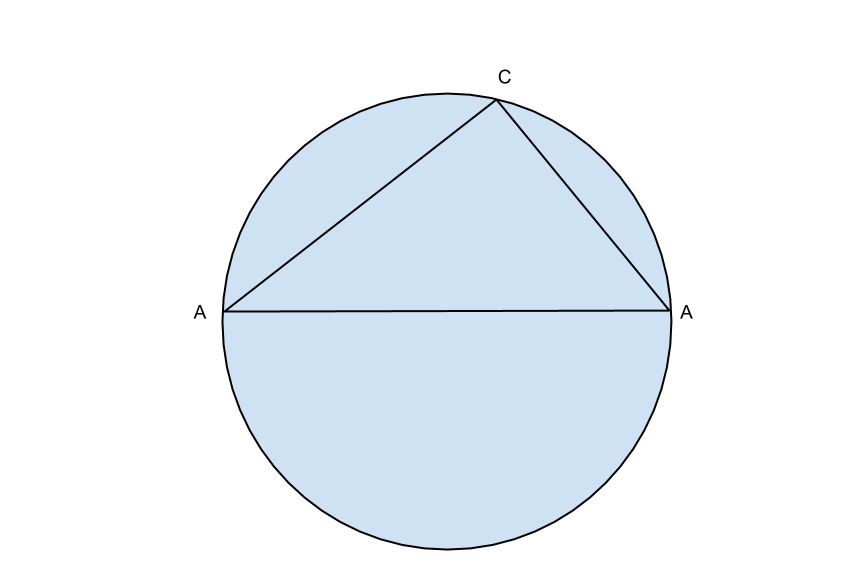
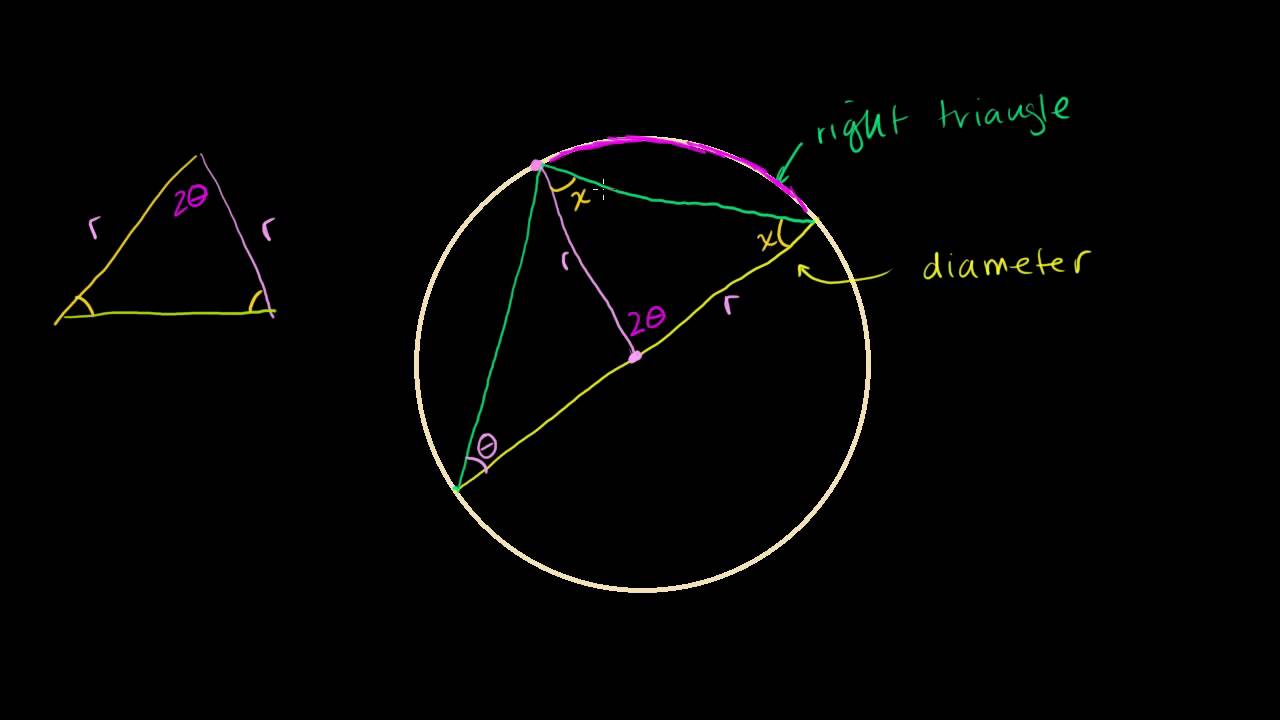
- Teorema di Talete: Il teorema di Talete stabilisce che se un triangolo è inscritto in un semicerchio (cioè, un lato del triangolo coincide con il diametro della circonferenza), allora quel triangolo è un triangolo rettangolo. Questo teorema è fondamentale per comprendere la relazione tra angoli retti e cerchi.
- Risoluzione di Problemi Geometrici: I triangoli rettangoli circoscritti offrono un framework concettuale per risolvere problemi geometrici complessi. Conoscere le proprietà di questi triangoli semplifica il calcolo di aree, angoli e lunghezze di lati in figure più elaborate.
- Ponte tra Geometria e Algebra: Lo studio di questi triangoli aiuta a collegare concetti geometrici a concetti algebrici, in particolare tramite il teorema di Pitagora e le relazioni trigonometriche.
Come afferma il Professor Giovanni Rossi, autore di "Geometria Elementare":
"La visualizzazione e la comprensione dei triangoli rettangoli circoscritti sono fondamentali per sviluppare un'intuizione geometrica solida. Questi triangoli servono da base per comprendere concetti più avanzati in geometria."
Impatto sugli Studenti
Per gli studenti, la comprensione dei triangoli rettangoli circoscritti può fare una grande differenza nel loro approccio alla geometria. Ecco alcuni benefici:
- Migliore Visualizzazione Spaziale: Permette di visualizzare meglio le figure geometriche e le loro proprietà.
- Pensiero Logico-Deduttivo: Incoraggia a sviluppare un pensiero logico-deduttivo per risolvere problemi geometrici.
- Preparazione per Concetti Avanzati: Fornisce una base solida per affrontare argomenti più complessi come la trigonometria e la geometria analitica.
Applicazioni Pratiche
Sebbene possano sembrare concetti puramente teorici, i triangoli rettangoli circoscritti hanno applicazioni pratiche sia a scuola che nella vita quotidiana:
- Architettura e Ingegneria: Gli architetti e gli ingegneri utilizzano i principi geometrici, inclusi quelli relativi ai triangoli rettangoli circoscritti, per progettare edifici, ponti e altre strutture.
- Navigazione: I principi della trigonometria, strettamente legati ai triangoli rettangoli, sono utilizzati nella navigazione marittima e aerea.
- Arte e Design: Le proporzioni e le relazioni geometriche basate sui triangoli rettangoli possono essere utilizzate per creare opere d'arte visivamente armoniose.
Un esempio semplice è la progettazione di un'area semicircolare in un giardino. Conoscendo il diametro, che coincide con l'ipotenusa del triangolo rettangolo inscritto, è possibile calcolare facilmente le dimensioni del triangolo da utilizzare per piantare fiori o posizionare elementi decorativi.
In conclusione, il triangolo rettangolo circoscritto è un concetto fondamentale nella geometria che ha implicazioni significative per la comprensione di concetti più avanzati e per applicazioni pratiche in diversi campi. Comprendere questo concetto contribuisce a sviluppare un pensiero logico e analitico, competenze preziose per la vita di ogni studente.