Triangolo Isoscele Altezza Relativa Al Lato Obliquo

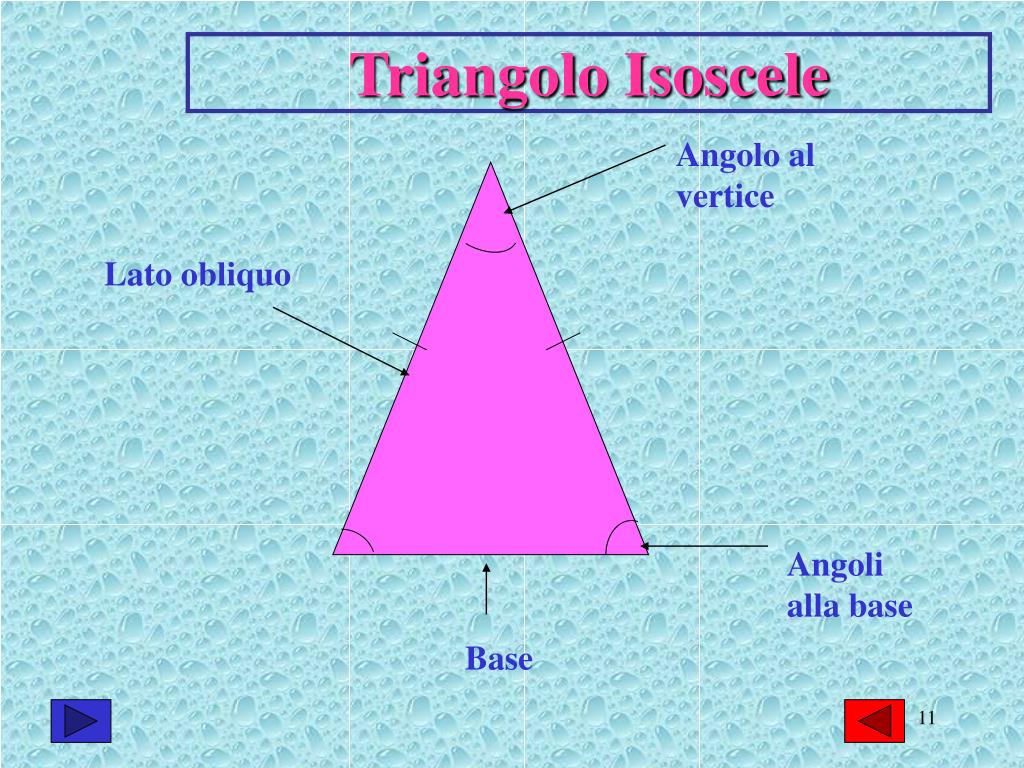
L'altezza relativa al lato obliquo in un triangolo isoscele è un segmento perpendicolare che congiunge un vertice della base con il lato obliquo opposto. Comprendere questa nozione è fondamentale per la risoluzione di problemi geometrici e per lo sviluppo del pensiero critico-analitico.

Definizione e Importanza

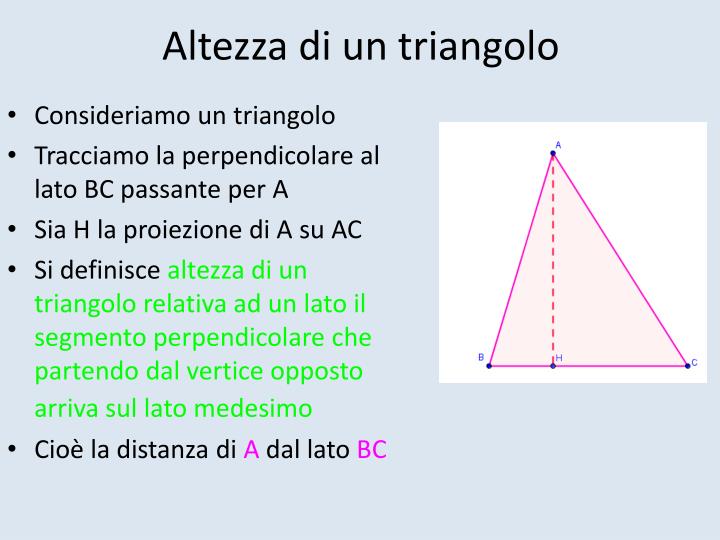
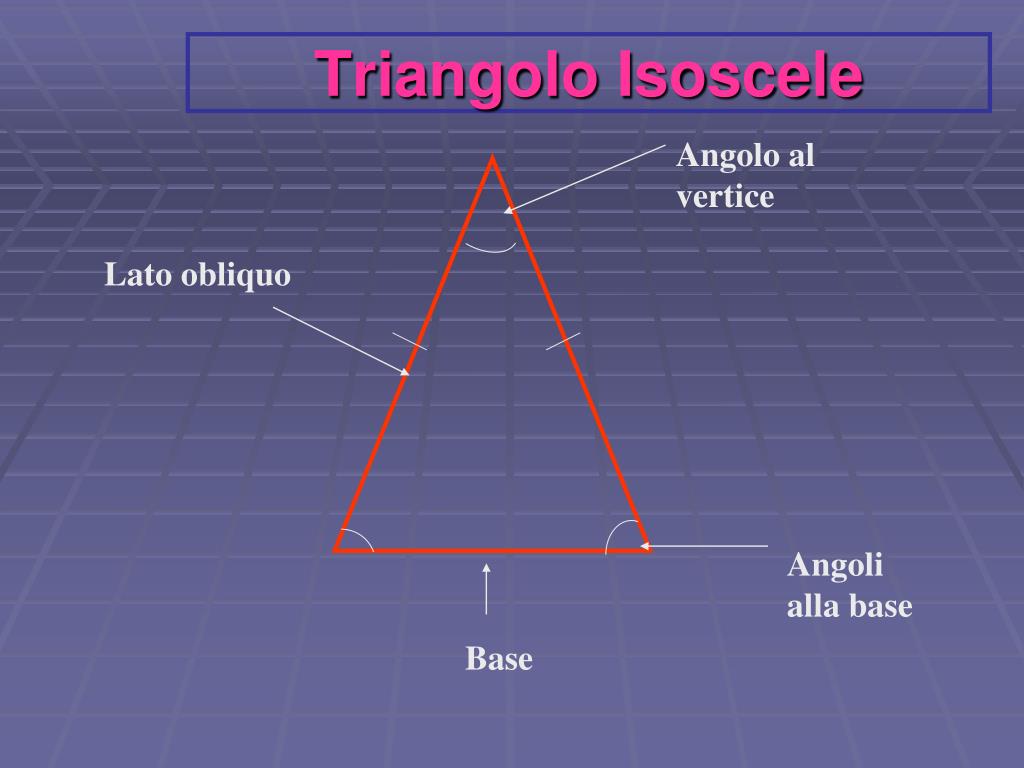
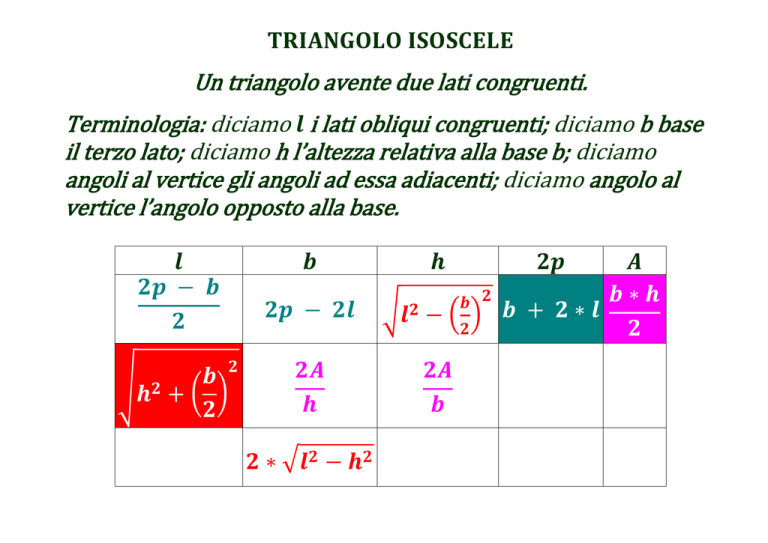
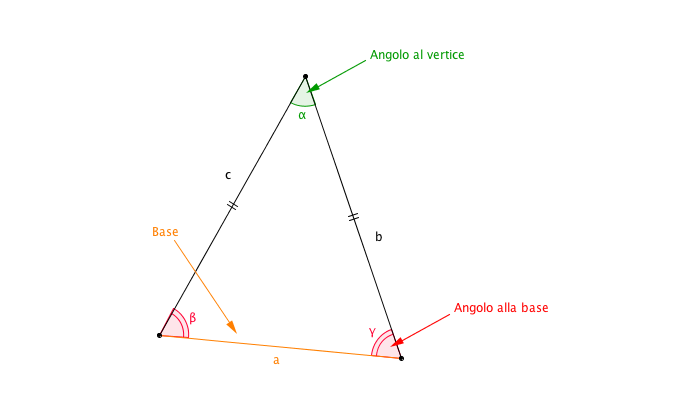
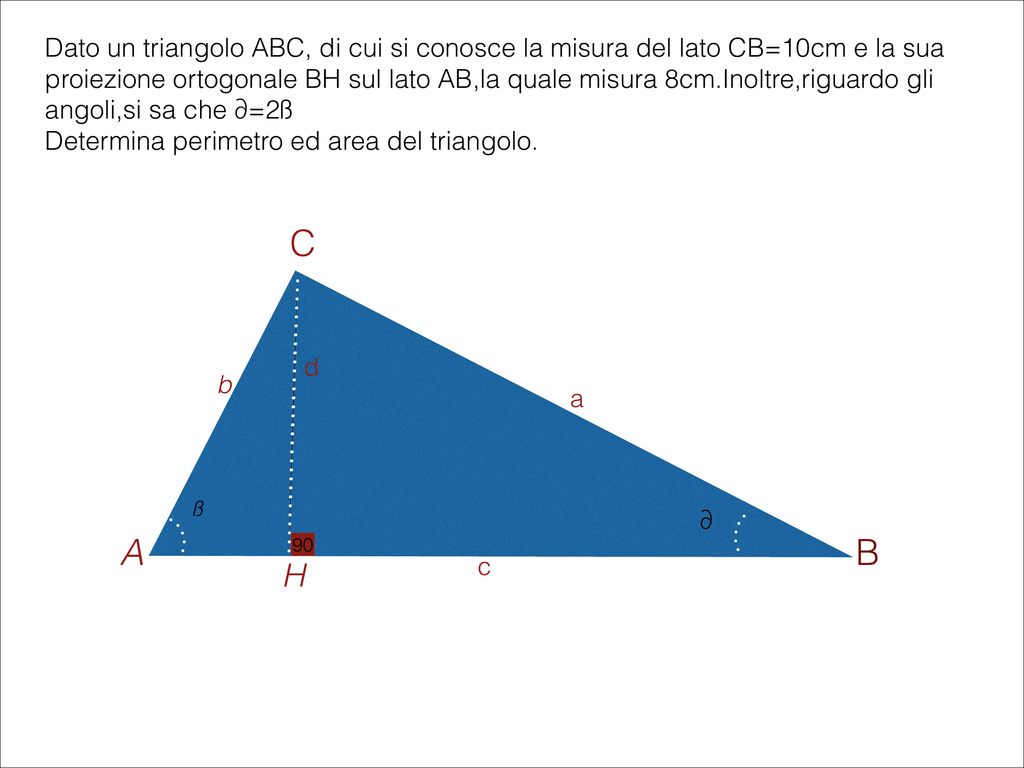
L'altezza di un triangolo, in generale, è il segmento perpendicolare tracciato da un vertice al lato opposto (o al suo prolungamento). Nel caso specifico di un triangolo isoscele, abbiamo due lati congruenti (lati obliqui) e un terzo lato, detto base. L'altezza relativa al lato obliquo è quindi il segmento perpendicolare che parte da uno dei vertici sulla base e interseca il lato obliquo opposto formando un angolo retto.

La rilevanza di questa specifica altezza risiede nella sua capacità di svelare relazioni geometriche nascoste all'interno del triangolo. Analizzandola, si possono individuare triangoli rettangoli congruenti, applicare il teorema di Pitagora e utilizzare le relazioni trigonometriche. La padronanza di questo concetto è dunque cruciale per la risoluzione di problemi di geometria euclidea.

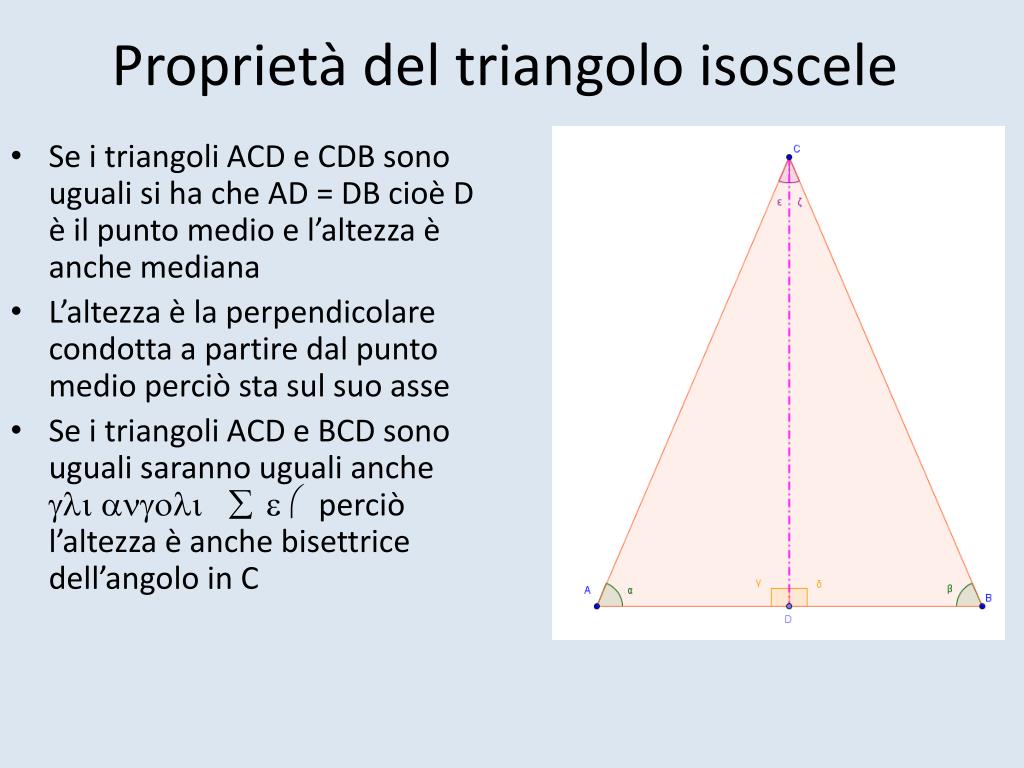
Inoltre, l'altezza relativa al lato obliquo è spesso collegata ad altre proprietà del triangolo isoscele, come gli angoli alla base (che sono congruenti) e l'asse della base (che coincide con l'altezza relativa alla base stessa). Comprendere come interagiscono questi elementi rafforza la comprensione complessiva della geometria del triangolo isoscele.

Perché è Importante per gli Studenti?

Per gli studenti, lo studio dell'altezza relativa al lato obliquo rappresenta una sfida stimolante. Richiede non solo la conoscenza delle definizioni fondamentali, ma anche la capacità di applicare tali conoscenze in contesti diversi e spesso non immediatamente evidenti. La risoluzione di problemi che coinvolgono questa altezza allena il ragionamento deduttivo, la capacità di visualizzazione spaziale e la precisione nel calcolo.

Affrontare con successo questi problemi aumenta la sicurezza in se stessi e la motivazione nello studio della matematica. Incoraggia inoltre ad adottare un approccio sistematico alla risoluzione di problemi, una competenza preziosa non solo in ambito scolastico, ma anche nella vita di tutti i giorni.

Applicazioni Pratiche

Le applicazioni pratiche del concetto di altezza relativa al lato obliquo, sebbene non sempre immediatamente visibili, sono numerose. In architettura, ad esempio, la progettazione di tetti spioventi o strutture triangolari richiede una conoscenza approfondita delle proprietà dei triangoli, inclusa la capacità di calcolare le altezze relative ai lati obliqui per garantire la stabilità e la resistenza della struttura.

Anche in ambito artistico, la comprensione delle proporzioni e delle relazioni geometriche all'interno di un triangolo isoscele può essere utile per la creazione di opere d'arte armoniose ed equilibrate. La prospettiva, ad esempio, si basa su principi geometrici che coinvolgono triangoli e proporzioni.

A livello scolastico, la conoscenza dell'altezza relativa al lato obliquo è fondamentale per la preparazione a esami e competizioni matematiche. I problemi che coinvolgono questo concetto sono spesso presenti in prove di ammissione a scuole superiori e università, e la loro corretta risoluzione dimostra una solida comprensione dei principi fondamentali della geometria.

"La geometria possiede due grandi tesori: uno è il teorema di Pitagora; l'altro, la divisione di una linea in media ed estrema ragione. Il primo possiamo paragonarlo a una misura d'oro; il secondo, a una gemma preziosa." - Johannes Kepler

Sebbene Kepler si riferisca a concetti più ampi, il suo pensiero sottolinea l'importanza di comprendere a fondo le relazioni geometriche, come quelle che legano l'altezza relativa al lato obliquo alle altre proprietà del triangolo isoscele.

In conclusione, lo studio dell'altezza relativa al lato obliquo in un triangolo isoscele non è solo un esercizio teorico, ma un'opportunità per sviluppare competenze di problem solving, ragionamento logico e visualizzazione spaziale che si rivelano preziose in molteplici contesti, sia scolastici che professionali.