Triangolo Con Tutti I Lati Uguali

Capita a tutti noi, prima o poi, di imbatterci in un problema di geometria che sembra ostico, o semplicemente di dimenticare le basi apprese a scuola. Non preoccuparti, è normale! In questo articolo, ci concentreremo su una figura geometrica fondamentale e affascinante: il triangolo equilatero. Lo analizzeremo in dettaglio, svelandone proprietà e applicazioni pratiche, rendendo il tutto accessibile e comprensibile anche a chi non ha una formazione matematica avanzata.

Cos'è un Triangolo Equilatero?

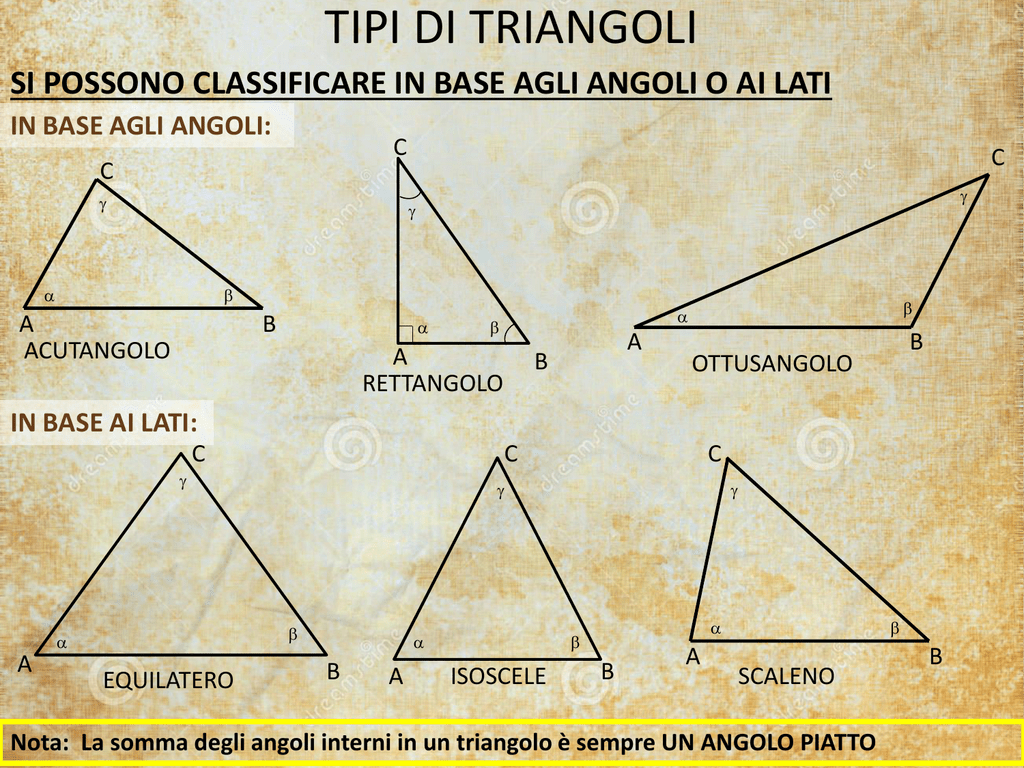
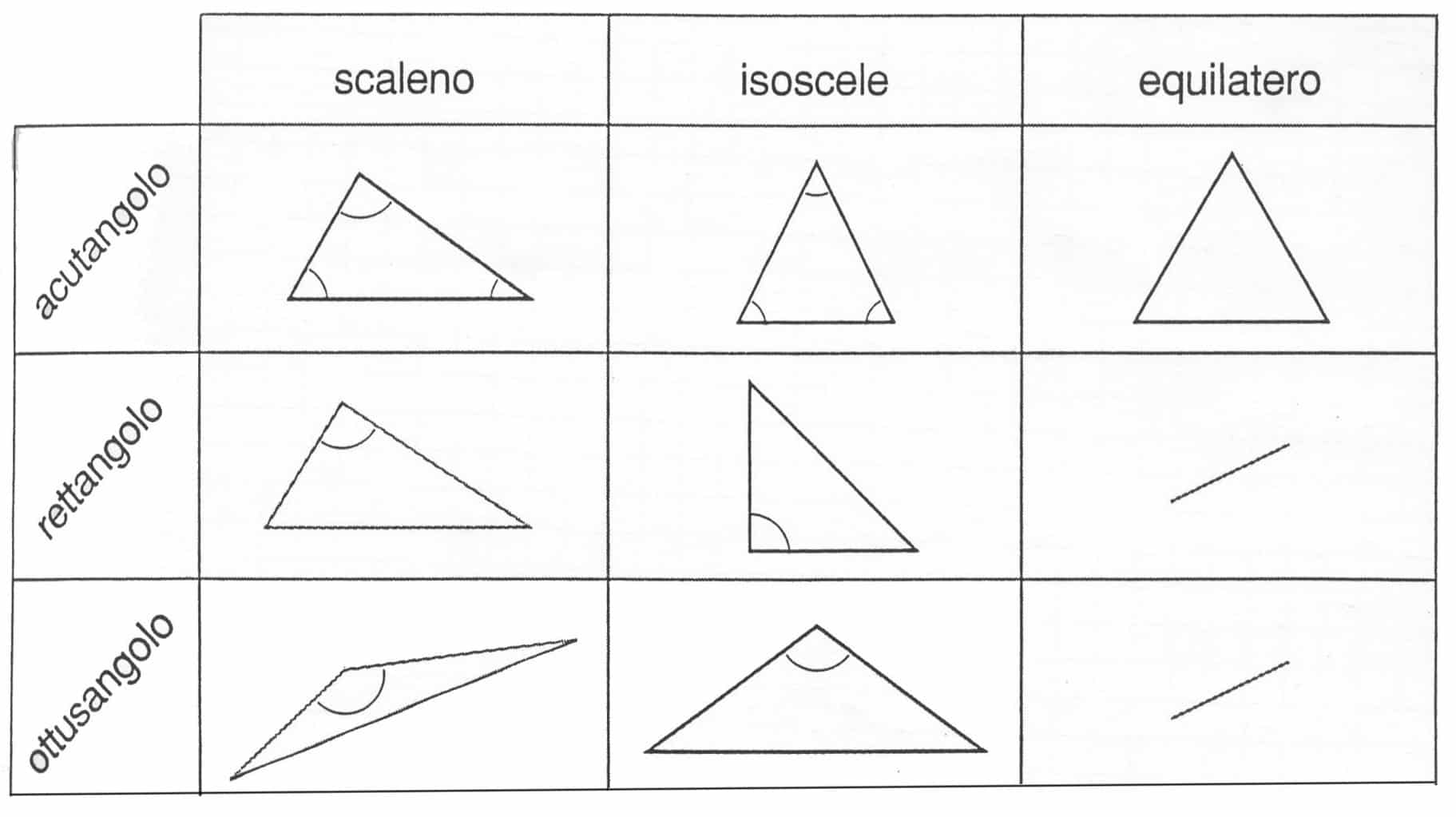
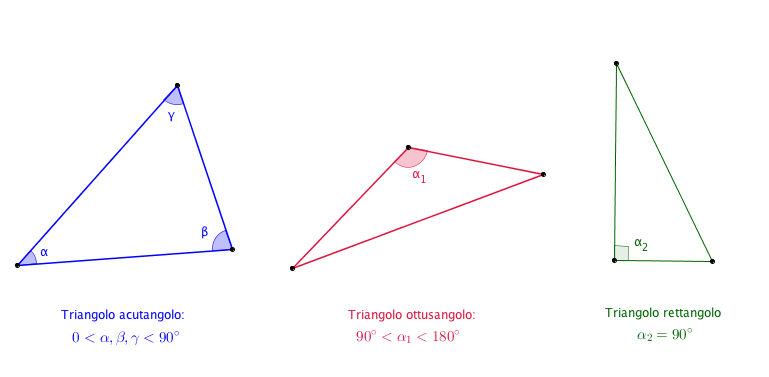
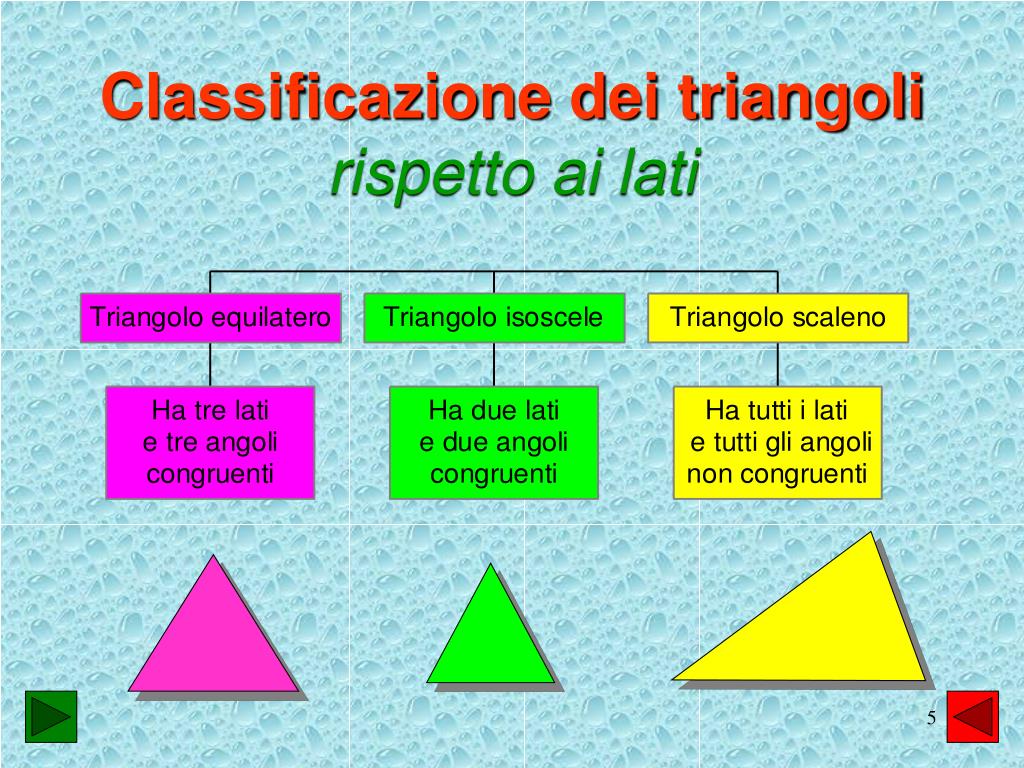
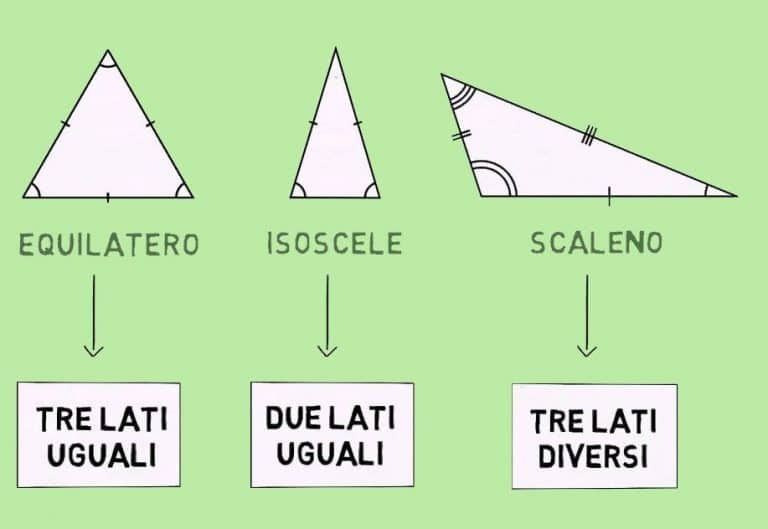
Un triangolo equilatero è un triangolo speciale che possiede una caratteristica ben precisa: tutti e tre i suoi lati sono uguali. Di conseguenza, anche tutti e tre i suoi angoli interni sono uguali e misurano ciascuno 60 gradi. Questa simmetria perfetta conferisce al triangolo equilatero proprietà uniche e lo rende una figura particolarmente importante in geometria e in diverse applicazioni pratiche.

Proprietà Fondamentali

• Lati uguali: Come già detto, la caratteristica distintiva è l'uguaglianza di tutti i lati.
• Angoli uguali: Tutti gli angoli interni misurano 60 gradi.
• Simmetria: Possiede tre assi di simmetria, uno per ogni vertice che passa per il punto medio del lato opposto.
• Altezza, mediana e bisettrice coincidono: In un triangolo equilatero, l'altezza, la mediana e la bisettrice relative a ciascun lato coincidono. Questo semplifica notevolmente i calcoli geometrici.

Impatto nel Mondo Reale

Potresti pensare che i triangoli equilateri siano solo un concetto teorico, ma la verità è che sono presenti in molteplici aspetti della nostra vita quotidiana. Non si tratta solo di formule matematiche astratte; parliamo di applicazioni concrete che influenzano il modo in cui viviamo e interagiamo con il mondo.

Architettura e Ingegneria

La forma del triangolo equilatero, grazie alla sua stabilità strutturale, viene spesso utilizzata in architettura e ingegneria. Ad esempio:

• Ponti: Strutture a traliccio utilizzano triangoli (spesso equilateri o isosceli) per distribuire il peso in modo uniforme e garantire la resistenza del ponte.
• Tetti: La forma di un tetto può essere influenzata dall'uso di triangoli equilateri per fornire supporto e resistenza alle intemperie.
• Geodetiche: Le cupole geodetiche, come quelle progettate da Buckminster Fuller, sono basate su una rete di triangoli, spesso equilateri o quasi equilateri, che offrono una straordinaria resistenza e leggerezza.

Design e Arte

La bellezza e la simmetria del triangolo equilatero lo rendono una scelta popolare anche nel design e nell'arte:

• Loghi: Molti loghi aziendali utilizzano forme triangolari, a volte implicitamente equilatere, per comunicare concetti come stabilità, forza e progresso.
• Mosaici e pavimentazioni: Il triangolo equilatero è una delle tre forme regolari che possono tassellare un piano (insieme al quadrato e all'esagono), il che significa che può essere utilizzato per creare pavimentazioni o mosaici senza lasciare spazi vuoti.
• Arte astratta: Artisti di diverse correnti hanno utilizzato il triangolo equilatero per le sue qualità estetiche e simboliche.

Scienza e Natura

Anche nel mondo naturale, la forma del triangolo equilatero si manifesta in modi sorprendenti:

• Cristalli: La struttura cristallina di alcuni minerali può presentare simmetrie triangolari.
• Molecole: Alcune molecole, come il trifluoruro di boro (BF3), hanno una forma triangolare planare con angoli di 120 gradi, derivata dalla geometria di un triangolo equilatero.

Affrontare le Obiezioni

Alcuni potrebbero sostenere che concentrarsi su una singola forma geometrica come il triangolo equilatero sia troppo limitante. È vero, il mondo è pieno di forme complesse e irregolari. Tuttavia, la comprensione delle figure geometriche di base, come il triangolo equilatero, fornisce le fondamenta per analizzare e comprendere forme più complesse. È come imparare l'alfabeto prima di poter leggere un libro: le basi sono essenziali.

Un'altra obiezione potrebbe riguardare l'utilità pratica della geometria nella vita di tutti i giorni. In un mondo dominato dalla tecnologia, alcuni potrebbero considerare la geometria come una disciplina obsoleta. Tuttavia, la geometria è alla base di molte tecnologie che utilizziamo quotidianamente, dalla progettazione di smartphone e computer alla navigazione GPS e alla grafica computerizzata. La comprensione dei principi geometrici è fondamentale per l'innovazione e lo sviluppo tecnologico.

Come Calcolare Area e Perimetro

Ora che abbiamo compreso cos'è un triangolo equilatero e dove lo troviamo, vediamo come calcolare le sue principali caratteristiche:

Perimetro

Il perimetro di un triangolo equilatero è semplicemente la somma della lunghezza dei suoi tre lati. Poiché tutti i lati sono uguali, la formula è molto semplice:

Perimetro = 3 * Lato

Ad esempio, se un triangolo equilatero ha un lato di 5 cm, il suo perimetro sarà 3 * 5 cm = 15 cm.

Area

Calcolare l'area è leggermente più complesso, ma esistono due metodi principali:

Metodo 1: Conoscendo l'altezza

Se conosciamo l'altezza (h) del triangolo, possiamo utilizzare la formula generale per l'area di un triangolo:

Area = (Base * Altezza) / 2

Poiché in un triangolo equilatero la base è semplicemente la lunghezza di un lato (l), la formula diventa:

Area = (l * h) / 2

Metodo 2: Conoscendo solo il lato

Se conosciamo solo la lunghezza del lato (l), possiamo calcolare l'area utilizzando la seguente formula:

Area = (√3 / 4) * l²

Questa formula deriva dal teorema di Pitagora e dalle proprietà dei triangoli 30-60-90, che si formano tracciando l'altezza in un triangolo equilatero.

Ad esempio, se un triangolo equilatero ha un lato di 4 cm, la sua area sarà (√3 / 4) * 4² = (√3 / 4) * 16 = 4√3 cm², che è circa 6.93 cm².

Semplificare Concetti Complessi

Immagina un triangolo equilatero come una piramide vista dall'alto. Ogni lato è come un supporto che contribuisce alla stabilità dell'intera struttura. Se un lato fosse più corto o più lungo degli altri, la piramide sarebbe instabile e tenderebbe a crollare. La perfetta uguaglianza dei lati e degli angoli garantisce la solidità e l'equilibrio.

Un altro esempio: pensa a una squadra di calcio. Se tutti i giocatori fossero bravi solo in attacco o solo in difesa, la squadra sarebbe sbilanciata. Per avere successo, è necessario un equilibrio tra le diverse abilità. Allo stesso modo, il triangolo equilatero rappresenta un equilibrio perfetto tra i suoi lati e i suoi angoli.

Soluzioni, Non Solo Problemi

Ora che abbiamo esplorato il triangolo equilatero in dettaglio, come possiamo applicare questa conoscenza per risolvere problemi concreti?

• Progettazione: Se sei un designer, puoi utilizzare la forma del triangolo equilatero per creare loghi o elementi grafici accattivanti ed equilibrati.
• Costruzioni: Se sei un ingegnere, puoi sfruttare la stabilità strutturale del triangolo equilatero per progettare ponti o edifici resistenti e sicuri.
• Matematica: Se sei uno studente, la comprensione del triangolo equilatero ti aiuterà a risolvere problemi di geometria più complessi e a sviluppare il tuo pensiero logico e analitico.

Il triangolo equilatero è una figura geometrica fondamentale che ci insegna l'importanza dell'equilibrio, della simmetria e della stabilità. La sua presenza in diversi ambiti, dall'architettura all'arte, dalla scienza alla natura, dimostra la sua rilevanza e il suo impatto sul mondo che ci circonda.

E ora, ti invito a riflettere: dove altro pensi di poter trovare triangoli equilateri nel tuo ambiente quotidiano? Cosa ti ha sorpreso di più di questa figura geometrica?