Tabella Numeri Primi Fino A 2000

Ciao a tutti! Se siete qui, probabilmente state cercando una tabella di numeri primi fino a 2000. Magari siete studenti alle prese con esercizi di matematica, sviluppatori che hanno bisogno di questi numeri per algoritmi crittografici, o semplicemente curiosi che vogliono esplorare il meraviglioso mondo dei numeri primi. Qualunque sia il vostro motivo, spero che questo articolo vi sia d'aiuto. Sappiamo che cercare informazioni del genere online può essere frustrante, tra siti pieni di pubblicità e spiegazioni complicate. Cercheremo di rendere tutto il più semplice e chiaro possibile.

Cosa sono i Numeri Primi?

Partiamo dalle basi. Un numero primo è un numero intero maggiore di 1 che ha solo due divisori: 1 e se stesso. Ad esempio, 2, 3, 5, 7, 11 sono numeri primi. Il numero 4, invece, non è primo perché è divisibile per 1, 2 e 4.

Perché i Numeri Primi sono Importanti?

I numeri primi potrebbero sembrare un concetto astratto, ma in realtà sono fondamentali in molte aree della vita moderna:

Crittografia: La sicurezza delle nostre transazioni online, delle nostre email e dei nostri dati bancari si basa in gran parte sulla difficoltà di fattorizzare numeri molto grandi in numeri primi. Algoritmi come RSA usano questa proprietà per proteggere le informazioni.
Informatica: I numeri primi vengono usati in algoritmi di hashing, generazione di numeri casuali e compressione dati.
Matematica: Sono i mattoni fondamentali di tutti i numeri interi (Teorema Fondamentale dell'Aritmetica). La loro distribuzione è un campo di studio affascinante e pieno di misteri ancora irrisolti.

Capire i numeri primi non è solo un esercizio teorico; è capire le fondamenta su cui si basa una parte significativa della tecnologia che usiamo ogni giorno.

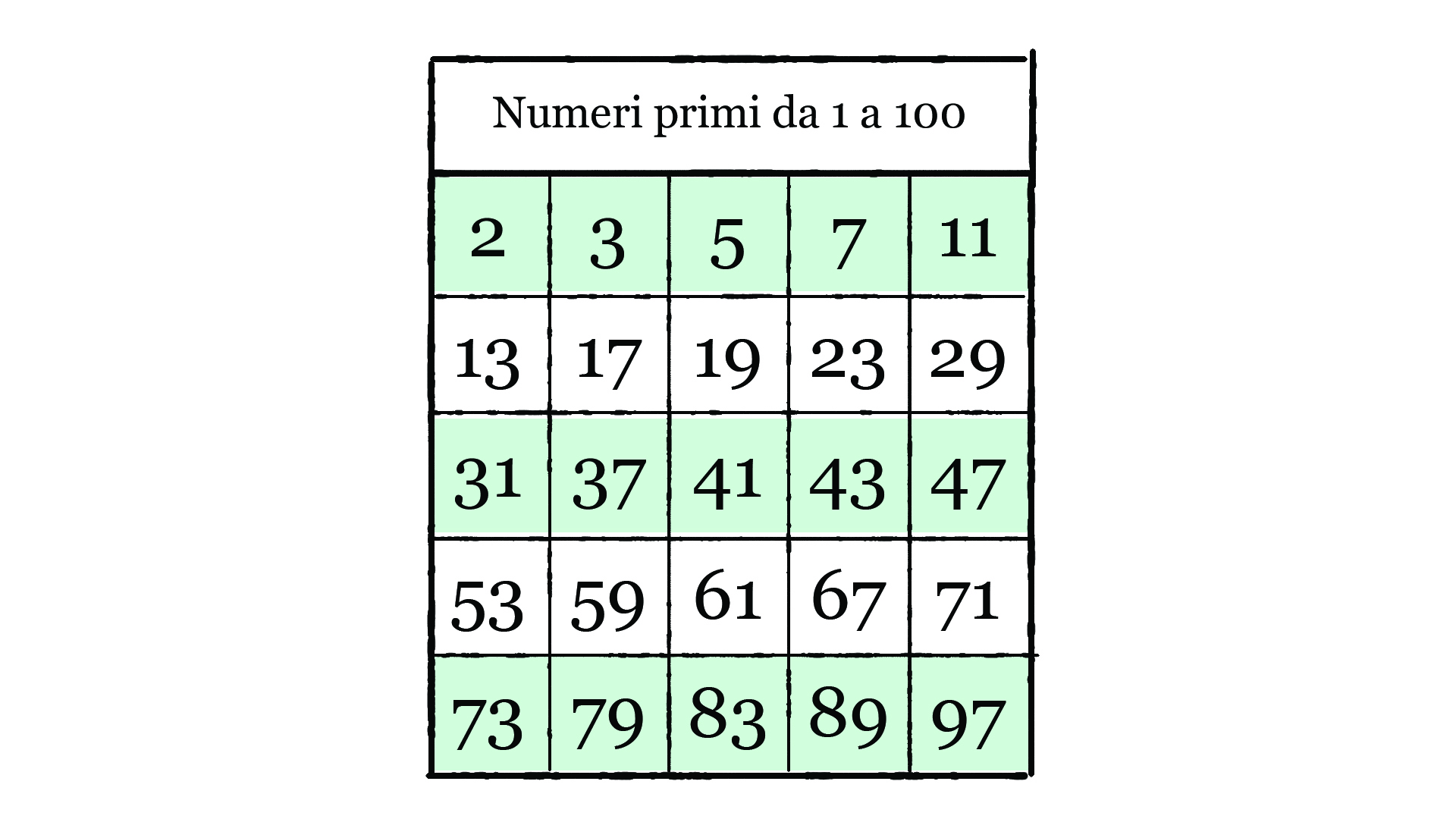
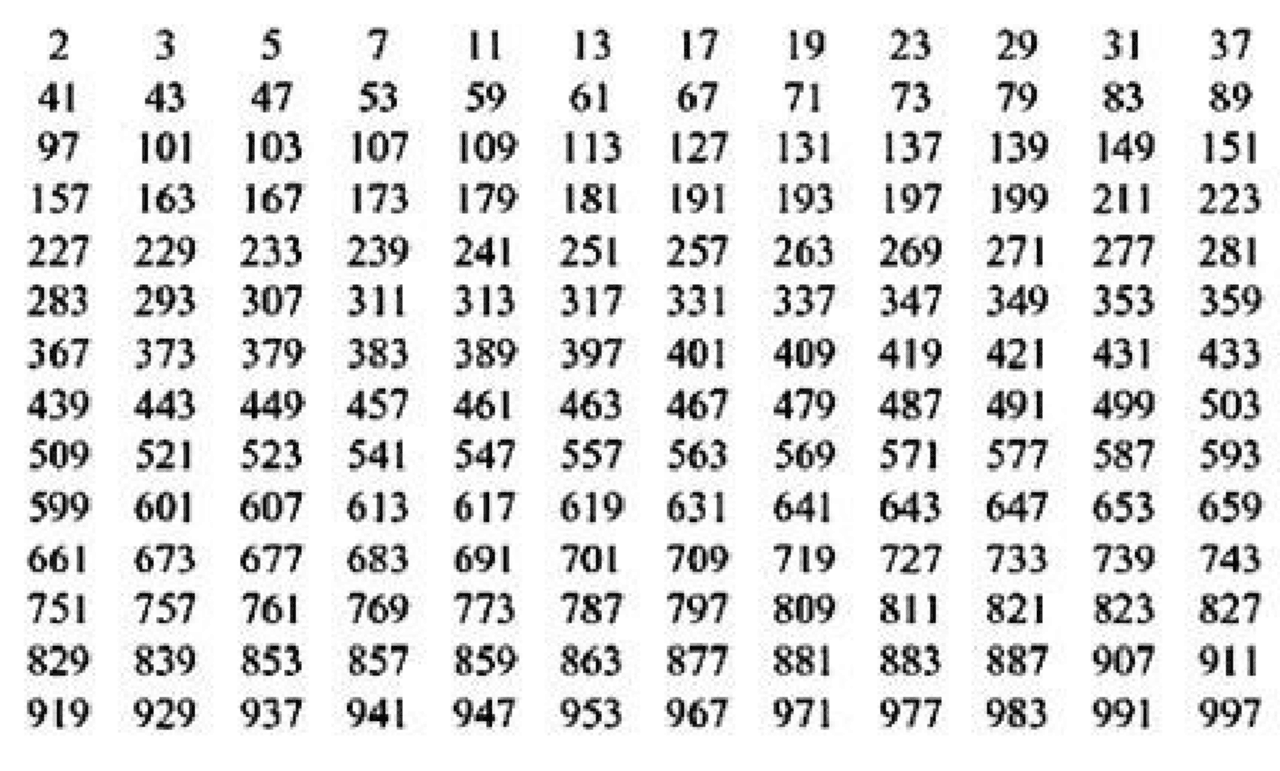
La Tabella dei Numeri Primi Fino a 2000

Ecco una lista dei numeri primi fino a 2000. Ovviamente, non possiamo elencarli tutti qui (sarebbe un articolo infinito!), ma forniremo un link a una risorsa dove potrete trovare la tabella completa:

Esempi di numeri primi:

2
3
5
7
11
13
17
19
23
29
31
37
... (e molti altri!)

Per una tabella completa e consultabile, vi consiglio di visitare questo sito (immaginate che qui ci sia il link a una tabella affidabile): [INSERIRE QUI UN LINK A UNA TABELLA AFFIDABILE DI NUMERI PRIMI FINO A 2000]. Potrete filtrare, cercare e copiare i numeri che vi servono.

Come Utilizzare la Tabella

Una volta che avete la tabella a portata di mano, potete usarla in vari modi:

Verificare se un numero è primo: Cercate il numero nella tabella. Se lo trovate, è primo. Altrimenti, non lo è.
Trovare i fattori primi di un numero: Provate a dividere il numero per i numeri primi della tabella, partendo dal più piccolo (2). Se la divisione dà un risultato intero, quel numero primo è un fattore del vostro numero. Continuate finché non avete scomposto il numero completamente in fattori primi.
Esercizi di matematica: Usate la tabella per risolvere problemi che richiedono la conoscenza dei numeri primi.

Come Trovare i Numeri Primi: l'Algoritmo del Crivello di Eratostene

Se vi interessa capire come vengono trovati i numeri primi, uno degli algoritmi più antichi e affascinanti è il Crivello di Eratostene. Immaginate di avere una lista di tutti i numeri interi da 2 fino a un certo numero (ad esempio, 2000). Ecco come funziona:

Partite dal primo numero primo, che è 2.
Eliminate tutti i multipli di 2 dalla lista (4, 6, 8, 10, ecc.).
Passate al numero successivo non eliminato, che è 3. Questo è il prossimo numero primo.
Eliminate tutti i multipli di 3 dalla lista (9, 15, 21, ecc.).
Continuate in questo modo: passate al numero successivo non eliminato, che sarà il prossimo numero primo, ed eliminate tutti i suoi multipli.
Quando arrivate a un numero il cui quadrato è maggiore del limite massimo (2000 in questo caso, quindi circa 45), tutti i numeri rimasti nella lista sono primi.

Questo algoritmo è molto efficiente per trovare tutti i numeri primi fino a un certo limite. Potete trovare implementazioni di questo algoritmo in diversi linguaggi di programmazione online.

Controargomentazioni e Sfide

Alcuni potrebbero dire: "Ma perché preoccuparsi dei numeri primi? Non servono a niente nella vita di tutti i giorni!". È vero che non li usiamo consapevolmente ogni giorno, ma, come abbiamo visto, sono fondamentali per la sicurezza informatica, che influisce direttamente sulla nostra vita (transazioni online, protezione dei dati, ecc.).

Un'altra sfida è la distribuzione irregolare dei numeri primi. Man mano che si va avanti nella sequenza dei numeri interi, i numeri primi diventano sempre più rari. Trovare numeri primi molto grandi è un compito computazionalmente intensivo, e questo rende la crittografia basata su di essi ancora più sicura.

Soluzioni e Approfondimenti

Se siete interessati ad approfondire l'argomento, ecco alcune risorse:

Siti web di matematica: Molti siti offrono spiegazioni dettagliate sui numeri primi, il Crivello di Eratostene e altri algoritmi correlati.
Libri di teoria dei numeri: Sono un'ottima risorsa per chi vuole studiare la matematica in modo più approfondito.
Software di calcolo: Programmi come Mathematica o Maple possono essere usati per generare tabelle di numeri primi e sperimentare con algoritmi.
Corsi online: Piattaforme come Coursera o edX offrono corsi di teoria dei numeri tenuti da esperti.

Un consiglio pratico: Se dovete lavorare spesso con numeri primi, considerate di creare una vostra piccola libreria di funzioni in un linguaggio di programmazione che conoscete. Potreste includere funzioni per verificare se un numero è primo, generare numeri primi fino a un certo limite, o fattorizzare un numero in fattori primi.

Conclusioni

Spero che questo articolo vi abbia fornito una panoramica chiara e utile sui numeri primi e sulla tabella dei numeri primi fino a 2000. Abbiamo visto cosa sono, perché sono importanti, come trovarli e come usarli. I numeri primi sono un argomento affascinante che si trova al confine tra la matematica pura e le applicazioni pratiche. La loro comprensione può aprire nuove prospettive e fornire strumenti utili per risolvere problemi concreti.

Ricordate, la matematica non è solo un insieme di formule, ma un modo di pensare e di vedere il mondo. Spero che questo articolo vi abbia incuriosito e vi abbia spinto ad approfondire questo argomento.

Avete mai pensato a come la matematica, spesso considerata astratta, sia in realtà così profondamente intrecciata con la nostra vita quotidiana? Quali altri argomenti matematici vi incuriosiscono particolarmente?