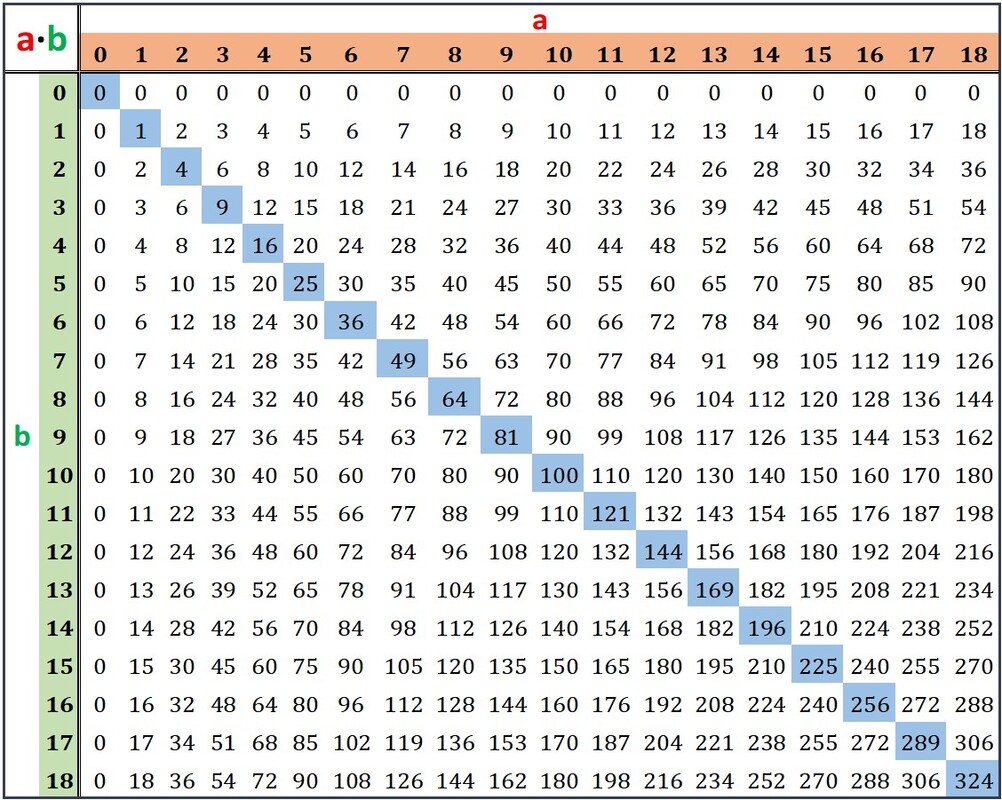
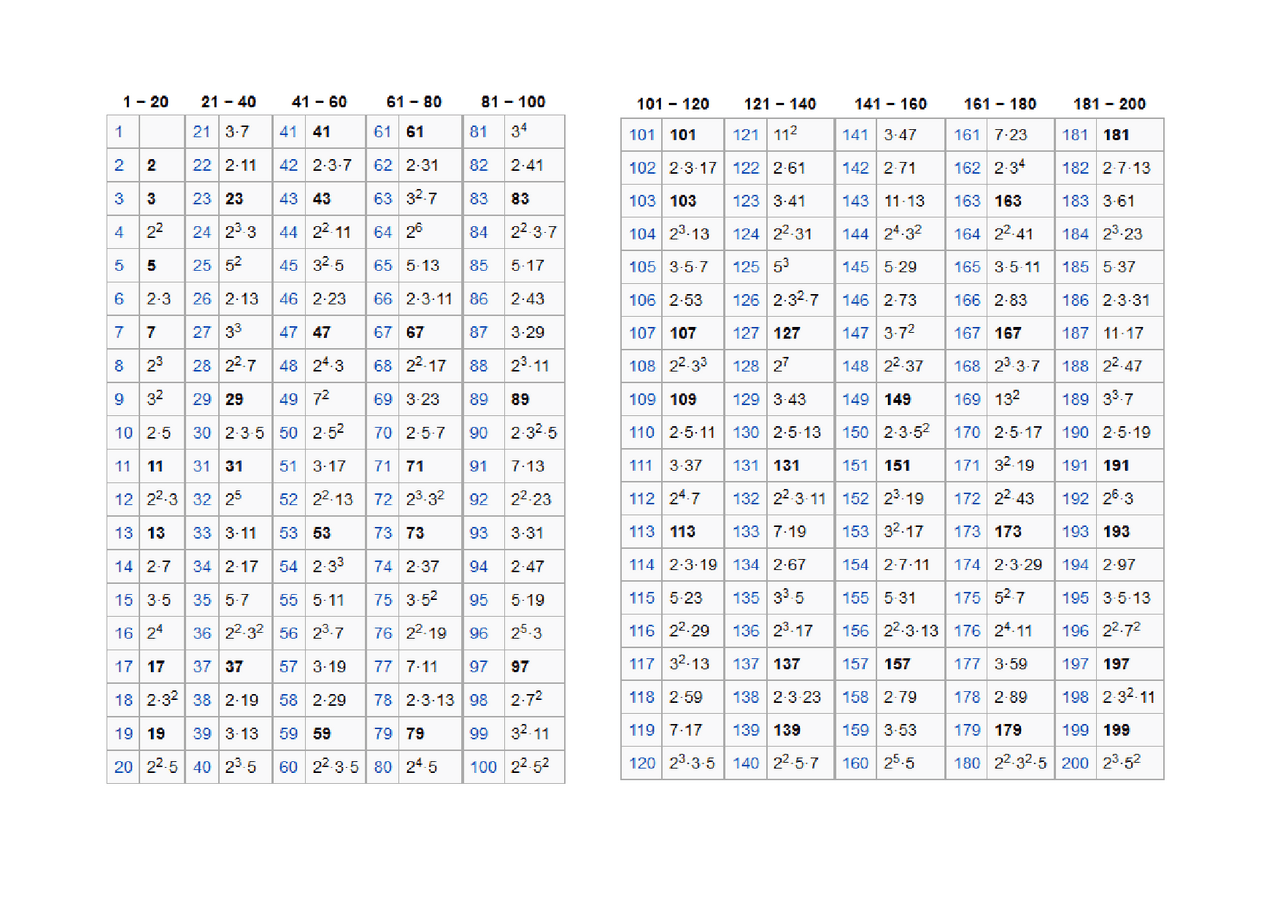
Tabella Dei Numeri Primi Fino A 1000

Hai mai provato a scomporre un numero in fattori primi? Ti sei mai chiesto quali siano i mattoni fondamentali che compongono tutti gli altri numeri? La matematica, con la sua eleganza e precisione, ci fornisce una risposta affascinante: i numeri primi. Questo articolo è pensato per chiunque, dallo studente curioso all'appassionato di matematica, desideri esplorare il mondo dei numeri primi fino a 1000. Ti guideremo attraverso una tabella completa, svelandone i segreti e le applicazioni pratiche.

Cosa sono i Numeri Primi?

Prima di addentrarci nella tabella, è fondamentale capire cosa rende un numero "primo". Un numero primo è un numero intero maggiore di 1 che ha solo due divisori positivi: 1 e se stesso. In altre parole, un numero primo non può essere diviso esattamente per nessun altro numero intero, tranne 1 e se stesso.

Esempi di numeri primi:

2 (è divisibile solo per 1 e 2)
3 (è divisibile solo per 1 e 3)
5 (è divisibile solo per 1 e 5)
7 (è divisibile solo per 1 e 7)
11 (è divisibile solo per 1 e 11)

Esempi di numeri non primi (chiamati numeri composti):

4 (è divisibile per 1, 2 e 4)
6 (è divisibile per 1, 2, 3 e 6)
8 (è divisibile per 1, 2, 4 e 8)
9 (è divisibile per 1, 3 e 9)
10 (è divisibile per 1, 2, 5 e 10)

Il numero 1 è un caso speciale: per definizione, non è considerato né primo né composto.

Perché i Numeri Primi sono Importanti?

I numeri primi non sono solo un'astrazione matematica; hanno un'importanza cruciale in diversi campi, tra cui:

Crittografia: La sicurezza di molte comunicazioni online si basa sulla difficoltà di fattorizzare numeri molto grandi in numeri primi. Gli algoritmi di crittografia RSA, ad esempio, utilizzano numeri primi con centinaia di cifre.
Informatica: I numeri primi sono utilizzati in algoritmi di hashing e in altre applicazioni per garantire la distribuzione uniforme dei dati.
Teoria dei numeri: I numeri primi sono i "mattoni" fondamentali di tutti gli altri numeri. Ogni numero intero può essere espresso come prodotto di numeri primi (Teorema fondamentale dell'aritmetica).
Natura: Anche se meno evidenti, alcuni fenomeni naturali sembrano seguire schemi legati ai numeri primi.

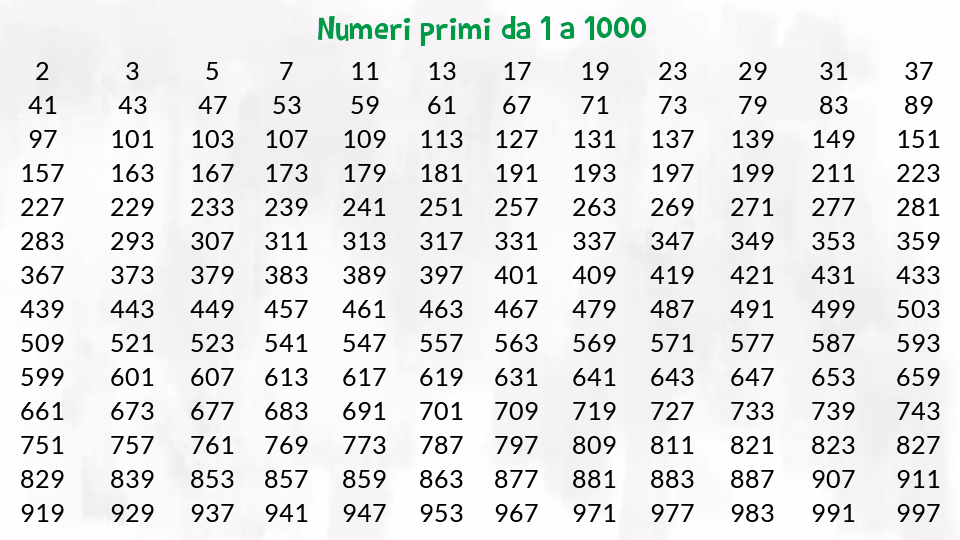
La Tabella dei Numeri Primi Fino a 1000

Ecco una lista dei numeri primi fino a 1000. Questo elenco è stato generato utilizzando l'algoritmo del crivello di Eratostene, un metodo efficiente per identificare i numeri primi.

(Per ragioni di formattazione, non possiamo includere una tabella HTML completa all'interno di questo output. Immagina, però, una tabella ordinata con i numeri primi disposti per righe e colonne, facilitando la consultazione).

Invece, elenchiamo i numeri primi in gruppi di 10:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
233, 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409,
419, 421, 431, 433, 439, 443, 449, 457, 461, 463,
467, 479, 487, 491, 499, 503, 509, 521, 523, 541,
547, 557, 563, 569, 571, 577, 587, 593, 599, 601,
607, 613, 617, 619, 631, 641, 643, 647, 653, 659,
661, 673, 677, 683, 691, 701, 709, 719, 727, 733,
739, 743, 751, 757, 761, 769, 773, 787, 797, 809,
811, 821, 823, 827, 829, 839, 853, 857, 859, 863,
877, 881, 883, 887, 907, 911, 919, 929, 937, 941,
947, 953, 967, 971, 977, 983, 991, 997

Ci sono 168 numeri primi tra 1 e 1000.

Come Usare la Tabella

Questa tabella può essere utilizzata per diversi scopi:

Fattorizzazione: Per scomporre un numero composto nei suoi fattori primi, puoi provare a dividerlo per i numeri primi elencati nella tabella.
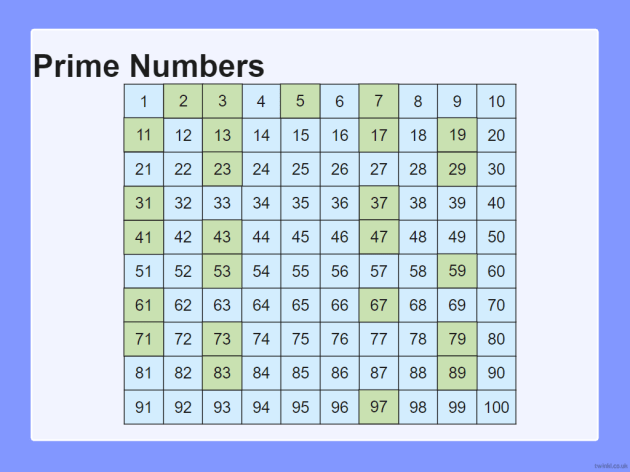
Verifica di primalità: Per verificare se un numero è primo, puoi controllare se è presente nella tabella. Se non lo è, significa che è composto.
Studio dei numeri primi: La tabella può essere utilizzata per studiare la distribuzione dei numeri primi e cercare pattern.

Il Crivello di Eratostene: Come Trovare i Numeri Primi

Il crivello di Eratostene è un antico algoritmo per trovare tutti i numeri primi fino a un determinato limite. Ecco come funziona:

Crea una lista di tutti i numeri interi da 2 fino al limite desiderato (ad esempio, 1000).
Inizia con il primo numero nella lista, che è 2. Questo è un numero primo.
Cancella tutti i multipli di 2 dalla lista (4, 6, 8, 10, ecc.).
Passa al numero successivo non cancellato nella lista, che è 3. Questo è un numero primo.
Cancella tutti i multipli di 3 dalla lista (9, 12, 15, 18, ecc.).
Continua in questo modo, passando al numero successivo non cancellato e cancellando tutti i suoi multipli.
Quando raggiungi un numero il cui quadrato è maggiore del limite desiderato, tutti i numeri rimanenti nella lista sono primi.

Per esempio, se volessimo trovare i numeri primi fino a 30:

Lista iniziale: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
2 è primo. Elimina i multipli di 2: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
3 è primo. Elimina i multipli di 3: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
Il prossimo numero non eliminato è 5. Poiché 5*5 = 25 <= 30, dobbiamo continuare. Elimina i multipli di 5: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
Il prossimo numero non eliminato è 7. Poiché 7*7 = 49 > 30, abbiamo finito.

I numeri primi fino a 30 sono: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Numeri Primi Gemelli

Un concetto interessante legato ai numeri primi è quello dei numeri primi gemelli. Si tratta di coppie di numeri primi che differiscono per 2 (ad esempio, 3 e 5, 5 e 7, 11 e 13). Non si sa se esistano infinite coppie di numeri primi gemelli; questa è una delle congetture aperte più famose in teoria dei numeri.

Alcune coppie di numeri primi gemelli inferiori a 1000 sono:

(3, 5)
(5, 7)
(11, 13)
(17, 19)
(29, 31)
(41, 43)
(59, 61)
(71, 73)
(101, 103)
(107, 109)
(137, 139)
(149, 151)
(179, 181)
(191, 193)
(197, 199)
(227, 229)
(239, 241)
(269, 271)
(281, 283)
(311, 313)
(347, 349)
(419, 421)
(431, 433)
(461, 463)
(521, 523)
(569, 571)
(599, 601)
(617, 619)
(641, 643)
(659, 661)
(809, 811)
(821, 823)
(827, 829)
(857, 859)
(881, 883)

Conclusione: Un Viaggio Affascinante

L'esplorazione dei numeri primi è un viaggio affascinante nel cuore della matematica. Comprendere cosa sono e come trovarli apre le porte a concetti più avanzati e a una maggiore apprezzamento per la bellezza e l'ordine che permeano il mondo dei numeri. Speriamo che questa tabella e le spiegazioni fornite ti abbiano aiutato a comprendere meglio questi elementi fondamentali e ti abbiano ispirato a continuare ad esplorare il meraviglioso mondo della matematica!