Simmetria Rispetto A Una Retta Formula

Ciao a tutti! La matematica a volte può sembrare un labirinto intricato, pieno di formule e concetti astratti. Ma non temete! Siamo qui per rendere l'apprendimento un'avventura stimolante e accessibile a tutti. Oggi, ci addentreremo nel mondo affascinante della simmetria rispetto a una retta, un concetto fondamentale in geometria che si manifesta ovunque intorno a noi, dalla natura all'arte e al design.

Se siete genitori che cercano di supportare i propri figli nello studio, o studenti che si sentono un po' persi, state tranquilli: questa guida è pensata apposta per voi. Useremo un linguaggio semplice e chiaro, evitando tecnicismi inutili, e illustreremo il concetto con esempi pratici e attività divertenti. Pronti? Partiamo!

Cos'è la Simmetria Rispetto a una Retta?

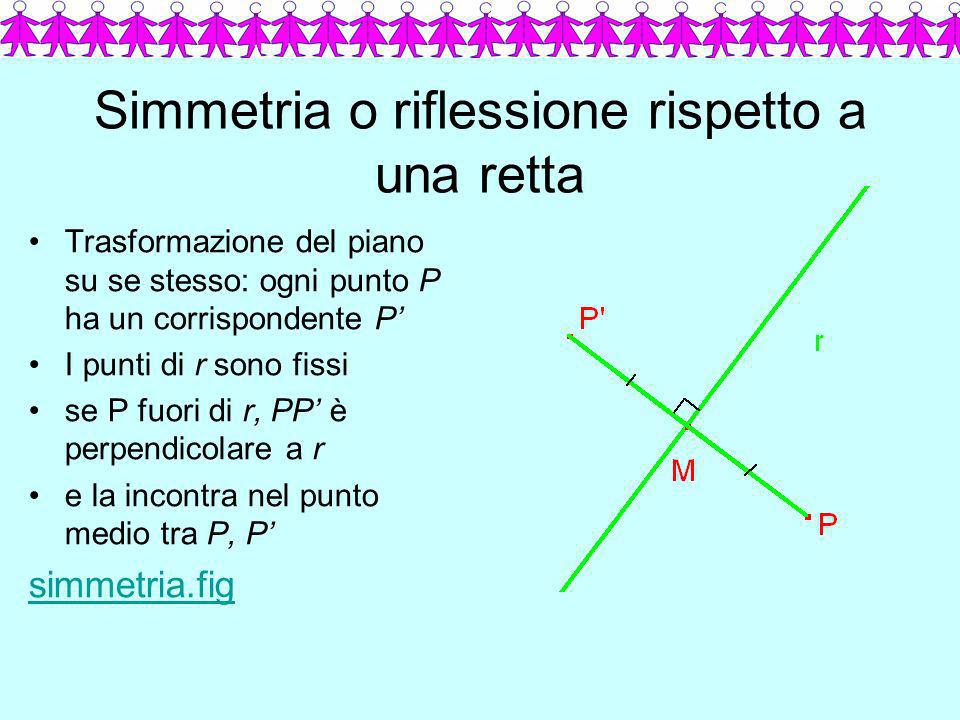
Immaginate di piegare un foglio di carta a metà e di disegnare una forma su una delle due metà. Se poi ricalcate la forma sull'altra metà, otterrete un'immagine speculare. La linea di piegatura rappresenta l'asse di simmetria, e la forma ricalcata è la sua immagine simmetrica rispetto a quella retta. In sostanza, la simmetria rispetto a una retta, o simmetria assiale, è una trasformazione geometrica che crea un'immagine speculare di una figura rispetto a una linea, chiamata asse di simmetria.

Più formalmente: ogni punto della figura originale ha un punto corrispondente nell'immagine simmetrica, tale che la retta che collega i due punti è perpendicolare all'asse di simmetria, e il punto di intersezione tra la retta e l'asse è il punto medio del segmento.

Esempi nella Vita Quotidiana

La simmetria è ovunque! Date un'occhiata al mondo che vi circonda:

* Farfalle: Le ali di una farfalla sono un esempio classico di simmetria assiale. La linea che divide il corpo della farfalla a metà è l'asse di simmetria. * Foglie: Molte foglie presentano una simmetria approssimativa rispetto alla nervatura centrale. * Volti umani: Anche se non siamo perfettamente simmetrici, i nostri volti mostrano una certa simmetria rispetto a una linea verticale che passa per il centro del naso. * Architettura: Molti edifici e monumenti, come il Taj Mahal, sono progettati con un'evidente simmetria per trasmettere un senso di equilibrio e armonia.

Come diceva il grande matematico Hermann Weyl nel suo libro "Simmetria": "Simmetria... è l'ordine riflesso nello spazio." Capire la simmetria, quindi, significa capire un ordine fondamentale che governa l'universo.

Come Trovare l'Immagine Simmetrica: La Formula e il Metodo

Ora che abbiamo capito cos'è la simmetria assiale, vediamo come trovare l'immagine simmetrica di un punto o di una figura rispetto a una retta. Non spaventatevi dalla parola "formula"! La spiegheremo passo dopo passo.

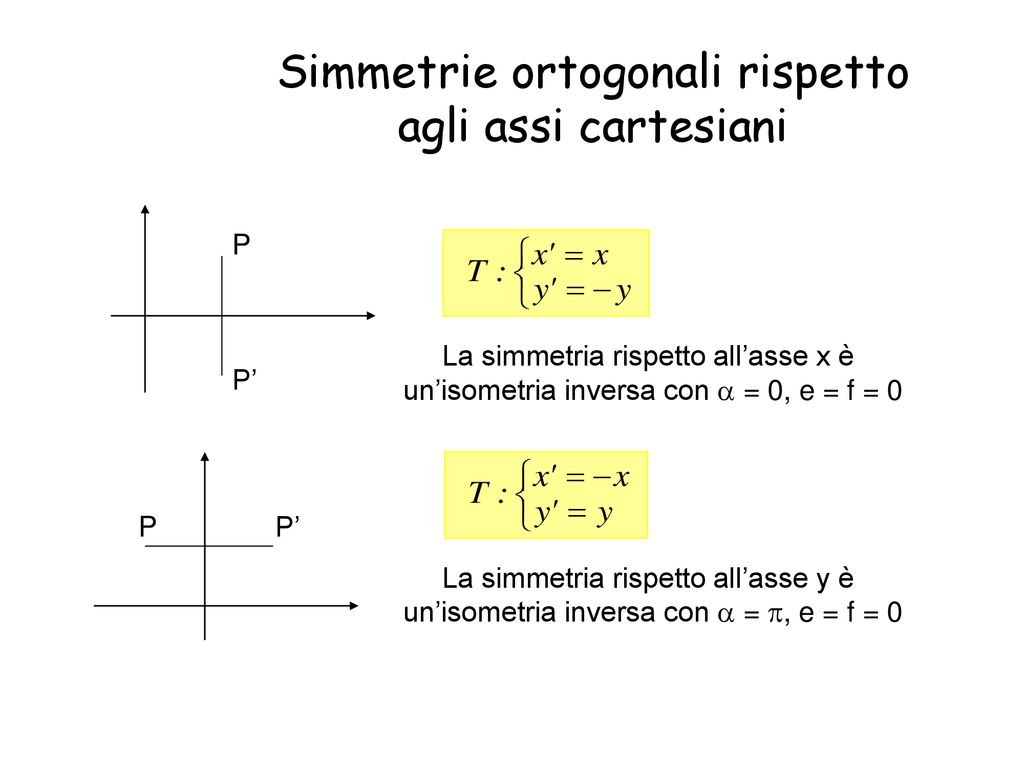
Consideriamo un punto P di coordinate (x, y) e una retta di equazione y = k (una retta orizzontale). L'immagine simmetrica P' di P rispetto alla retta y = k avrà coordinate (x', y') tali che:

* x' = x (l'ascissa rimane la stessa) * y' = 2k - y (l'ordinata cambia secondo questa formula)

Spiegazione: La distanza tra il punto P e la retta y = k è la stessa della distanza tra la retta y = k e il punto P'. La formula 2k - y esprime proprio questo concetto. Si calcola 2 volte il valore di k (l'ordinata della retta), e si sottrae l'ordinata originale (y).

Esempio: Supponiamo di avere il punto P(3, 2) e la retta y = 5. Vogliamo trovare l'immagine simmetrica P' di P rispetto a questa retta. Usando la formula:

* x' = 3 * y' = 2 * 5 - 2 = 10 - 2 = 8

Quindi, l'immagine simmetrica P' ha coordinate (3, 8).

Se la retta è verticale, di equazione x = h, allora la formula cambia:

* x' = 2h - x * y' = y

Importante: Questa è la formula più semplice per la simmetria rispetto ad assi orizzontali e verticali. Per assi obliqui, la formula diventa più complessa, ma il principio rimane lo stesso: trovare il punto tale che la retta sia l'asse del segmento che unisce il punto originale e la sua immagine.

Passi Pratici per Trovare l'Immagine Simmetrica

Identificare l'asse di simmetria: Determinare l'equazione della retta rispetto alla quale si vuole trovare l'immagine simmetrica.
Scegliere il punto o la figura: Individuare il punto o la figura di cui si vuole calcolare l'immagine speculare. Se si tratta di una figura, è sufficiente trovare l'immagine simmetrica di alcuni punti chiave (ad esempio, i vertici) e collegarli.
Applicare la formula (o il metodo geometrico): Utilizzare la formula appropriata (a seconda se l'asse è orizzontale, verticale o obliquo) per calcolare le coordinate dell'immagine simmetrica. In alternativa, si può utilizzare un metodo geometrico, disegnando la perpendicolare all'asse di simmetria passante per il punto, e misurando la distanza dal punto all'asse per riportarla dall'altra parte.
Disegnare l'immagine simmetrica: Una volta trovati i punti dell'immagine simmetrica, collegarli per ottenere la figura speculare.

Esercizi e Attività Pratiche

La teoria è importante, ma la pratica è fondamentale per consolidare la comprensione. Ecco alcune attività e esercizi che potete fare per esercitarvi:

* Disegno con la simmetria: Prendete un foglio di carta, piegatelo a metà e disegnate una forma su una delle due metà. Ricalcate la forma sull'altra metà per creare l'immagine simmetrica. Provate con forme diverse e con assi di simmetria diversi (verticale, orizzontale, obliquo). * Simmetria con lo specchio: Mettete uno specchio su un foglio di carta e disegnate una forma su un lato dello specchio. L'immagine riflessa nello specchio è l'immagine simmetrica della forma. * Esercizi con le coordinate: Prendete un piano cartesiano e disegnate alcuni punti e una retta. Calcolate l'immagine simmetrica di ogni punto rispetto alla retta usando la formula. * Software di geometria: Esistono molti software di geometria dinamica (come GeoGebra) che permettono di visualizzare e manipolare la simmetria in modo interattivo. Provate a creare figure e a trovare le loro immagini simmetriche rispetto a diverse rette.

Esempio di esercizio: Dato il punto A(1,3) e la retta y = 2, trovare le coordinate del punto A', simmetrico di A rispetto alla retta data.

Soluzione: x' = 1 (l'ascissa rimane invariata) y' = 2*2 - 3 = 4 - 3 = 1 Quindi A' (1, 1)

Consigli per Genitori e Studenti

Genitori, incoraggiate i vostri figli a esplorare la simmetria nel mondo che li circonda. Fate loro notare le simmetrie negli oggetti, negli edifici, nella natura. Giocate insieme a creare disegni simmetrici. Trasformate l'apprendimento in un'attività divertente e interattiva.

Studenti, non abbiate paura di chiedere aiuto se avete difficoltà. La matematica richiede pazienza e perseveranza. Non scoraggiatevi di fronte agli ostacoli, ma vedeteli come opportunità per imparare e crescere. Ricordatevi che la simmetria è un concetto fondamentale che vi sarà utile in molti altri ambiti della matematica e della scienza. Come afferma Carol Dweck, psicologa e autrice del libro "Mindset: The New Psychology of Success", "La crescita deriva dall'affrontare le sfide, non dall'evitarle."

Un consiglio extra: create una mappa mentale dei concetti chiave. Questo vi aiuterà a visualizzare le connessioni tra i diversi argomenti e a memorizzare le informazioni in modo più efficace.

Conclusione: Abbracciare la Bellezza della Simmetria

La simmetria rispetto a una retta è molto più di una semplice formula matematica. È un concetto che rivela l'ordine e l'armonia che si celano dietro la complessità del mondo. Spero che questa guida vi abbia aiutato a comprendere meglio questo concetto e a sviluppare un apprezzamento per la bellezza della simmetria. Ricordate, la matematica è un'avventura, non una competizione. Divertitevi ad esplorare, a sperimentare e a scoprire le meraviglie del mondo che vi circonda. E non dimenticate: la simmetria è ovunque, basta saperla vedere!

Ora tocca a voi! Mettete in pratica quello che avete imparato, esplorate il mondo con occhi nuovi e scoprite la bellezza della simmetria in ogni cosa.