Serie Di Fibonacci Primi 100 Numeri

Ti sei mai chiesto cosa si nasconde dietro una sequenza di numeri apparentemente semplice? Parliamo della Serie di Fibonacci, una successione matematica che si manifesta in modi sorprendenti nella natura, nell'arte e persino nella finanza. In questo articolo, esploreremo i primi 100 numeri di Fibonacci, analizzando le loro caratteristiche e il fascino che li circonda. Questo articolo è rivolto a studenti, appassionati di matematica, curiosi di natura e chiunque voglia scoprire la bellezza celata nei numeri. Preparati per un viaggio affascinante!

Cos'è la Serie di Fibonacci?

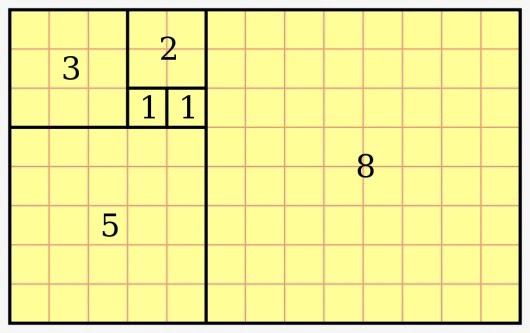
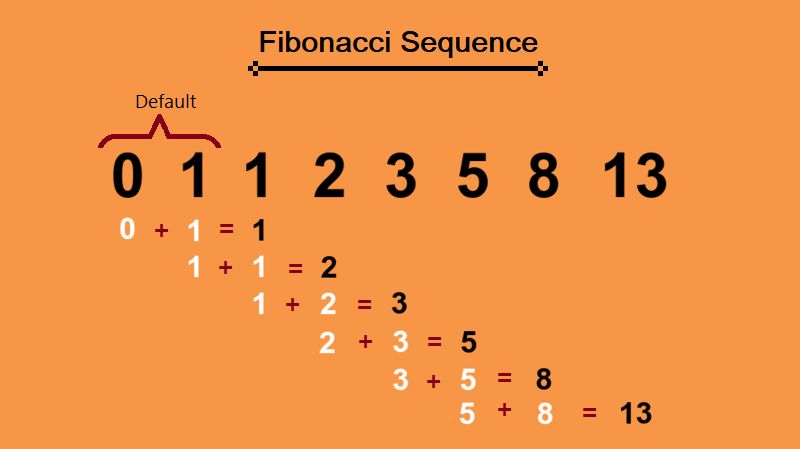
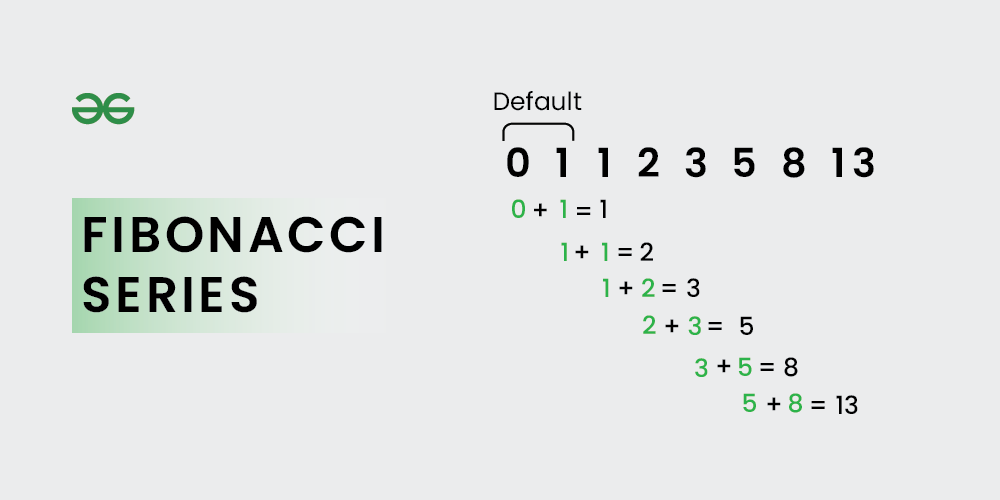
La Serie di Fibonacci è una sequenza di numeri in cui ogni numero è la somma dei due numeri precedenti. La sequenza inizia convenzionalmente con 0 e 1, quindi il terzo numero è 0 + 1 = 1, il quarto è 1 + 1 = 2, e così via. La formula matematica che la definisce è:

F(n) = F(n-1) + F(n-2)

Dove:

F(n) è l'n-esimo numero di Fibonacci.
F(n-1) è il numero di Fibonacci precedente.
F(n-2) è il numero di Fibonacci due posizioni indietro.

In pratica, partendo da F(0) = 0 e F(1) = 1, possiamo generare l'intera sequenza.

I Primi 100 Numeri di Fibonacci

Ecco i primi 100 numeri di Fibonacci. Elencarli tutti in linea sarebbe poco leggibile, quindi li suddivideremo in gruppi per una consultazione più agevole. Nota come crescono rapidamente! La velocità di crescita è un elemento chiave della Serie di Fibonacci. Presta attenzione a come aumentano esponenzialmente!

Nota: Elencare tutti i numeri qui renderebbe l'articolo lunghissimo. Invece, presenteremo una tabella riassuntiva e una discussione sulla loro crescita.

Come Calcolare i Numeri di Fibonacci

Esistono diversi modi per calcolare i numeri di Fibonacci:

Metodo Ricorsivo: È la traduzione diretta della formula. Funziona bene per piccoli numeri, ma diventa inefficiente per numeri più grandi a causa dei calcoli ripetuti.
Metodo Iterativo: Utilizza un ciclo per calcolare i numeri di Fibonacci in sequenza, memorizzando i risultati precedenti. È molto più efficiente del metodo ricorsivo.
Formula di Binet: Una formula diretta che permette di calcolare l'n-esimo numero di Fibonacci senza dover calcolare i numeri precedenti. Tuttavia, può introdurre errori di arrotondamento per numeri molto grandi.

Per calcolare i primi 100 numeri, il metodo iterativo è sicuramente la scelta più pratica ed efficiente.

Il Rapporto Aureo (Phi) e la Serie di Fibonacci

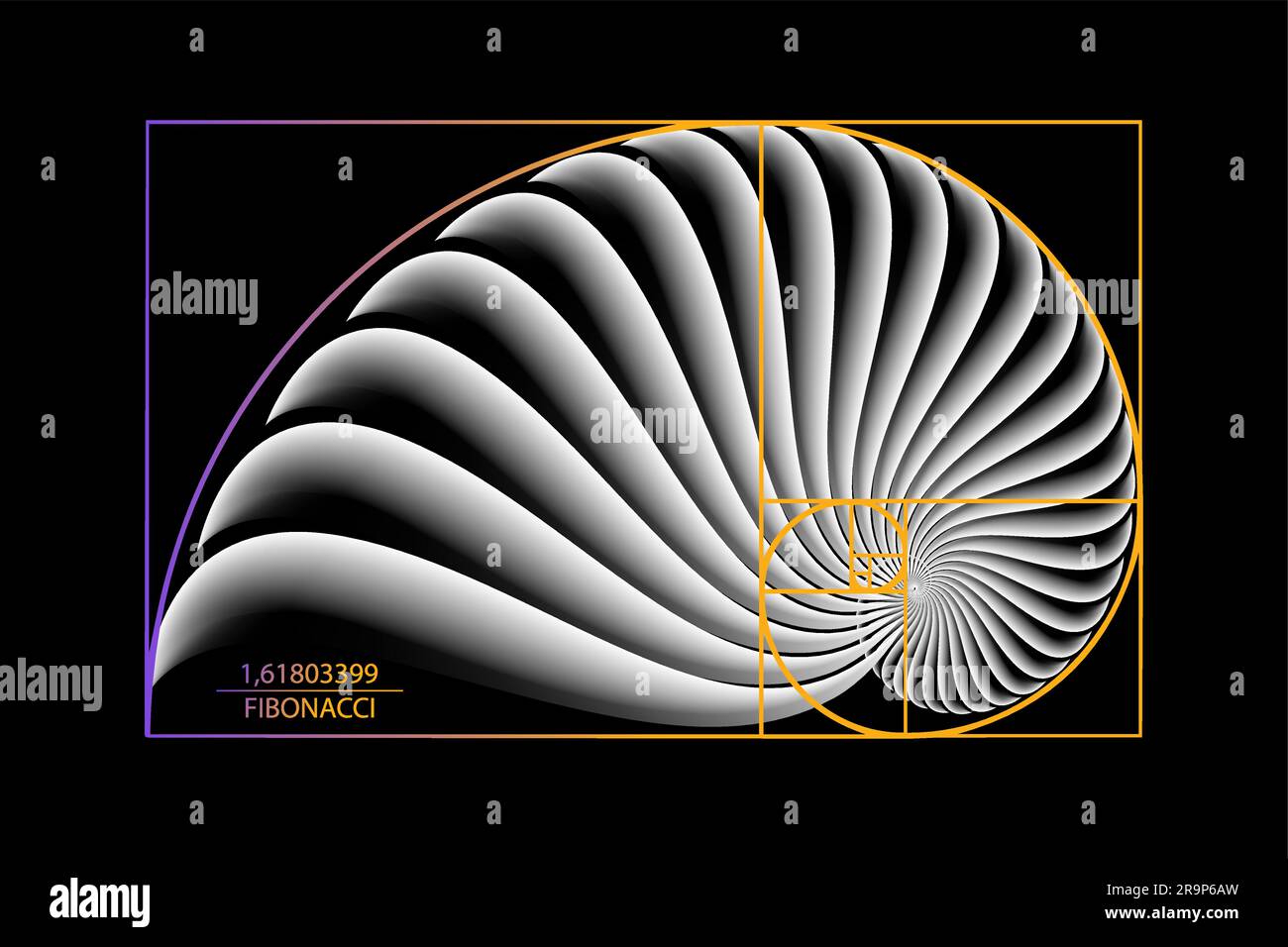
Uno degli aspetti più affascinanti della Serie di Fibonacci è la sua stretta relazione con il Rapporto Aureo, spesso indicato con la lettera greca Phi (Φ). Il Rapporto Aureo è un numero irrazionale approssimativamente uguale a 1.6180339887...

Se dividiamo un numero di Fibonacci per il numero di Fibonacci precedente, otteniamo un valore che si avvicina sempre di più a Phi man mano che i numeri diventano più grandi. Ad esempio:

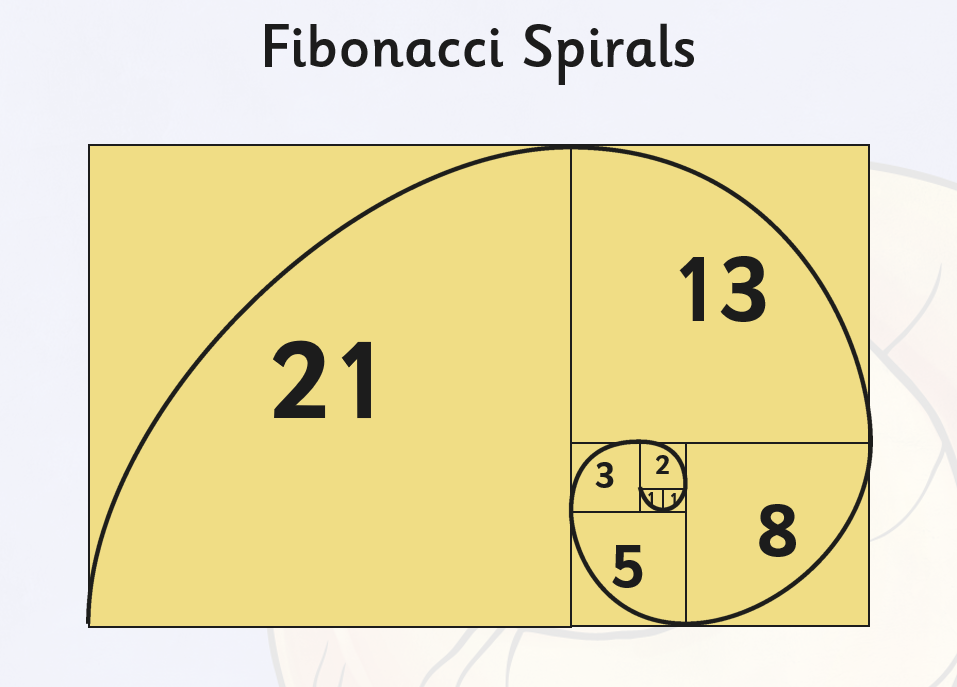
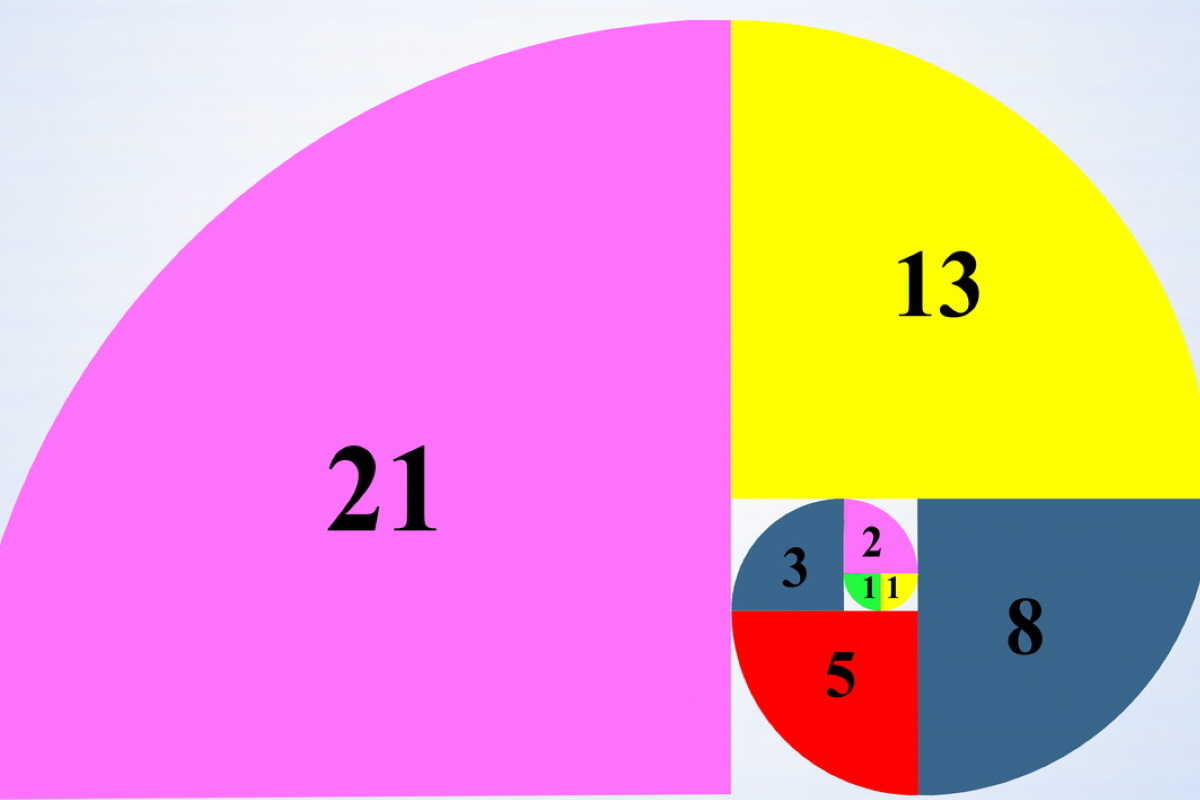
8 / 5 = 1.6
13 / 8 = 1.625
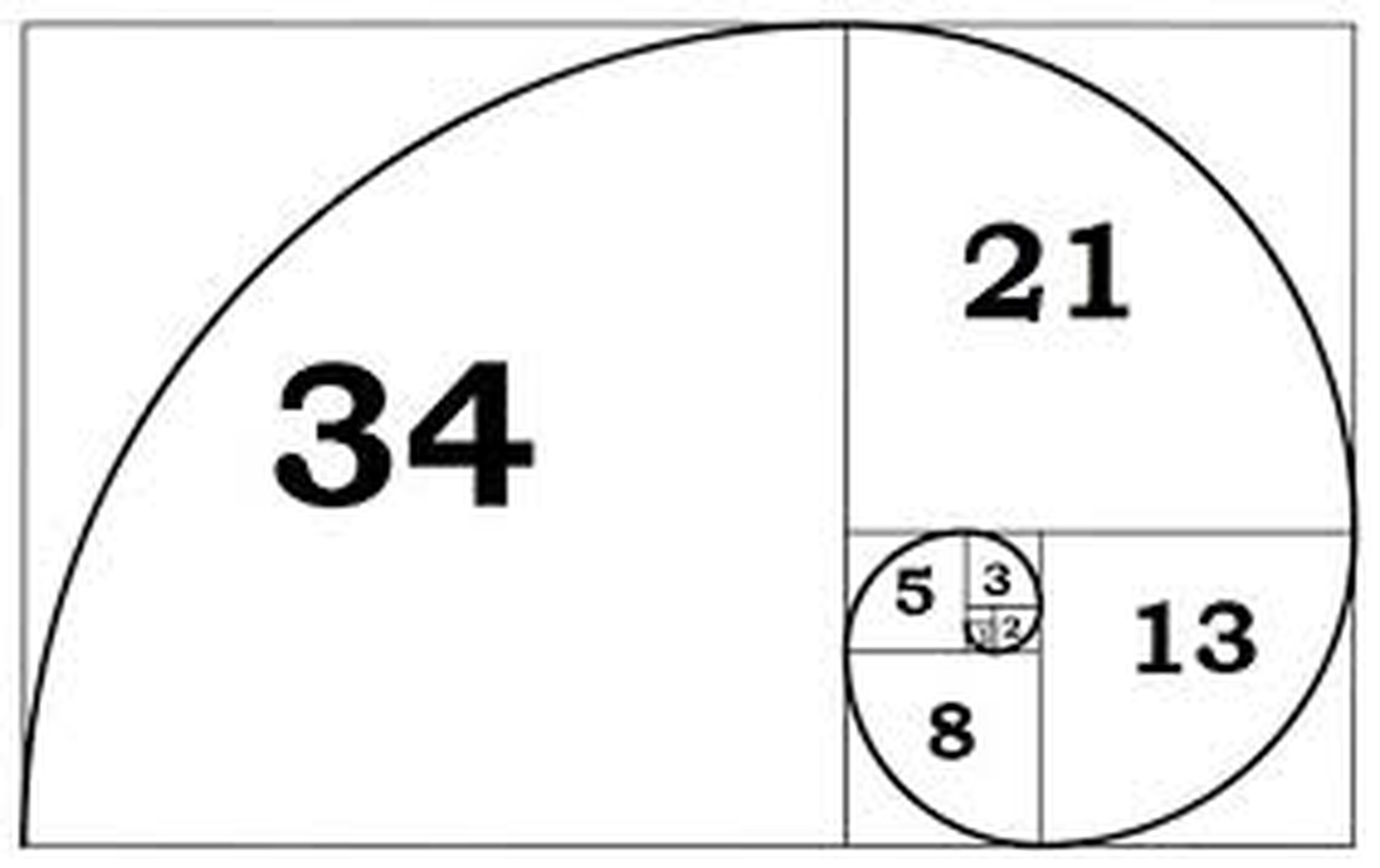
21 / 13 = 1.61538...
34 / 21 = 1.61904...

Questa convergenza verso il Rapporto Aureo è una delle ragioni per cui la Serie di Fibonacci è così importante e presente in natura.

La Serie di Fibonacci in Natura

La Serie di Fibonacci si manifesta in innumerevoli forme in natura. Alcuni esempi includono:

La disposizione delle foglie su uno stelo: Spesso, le foglie sono disposte in modo da massimizzare l'esposizione alla luce solare, e questa disposizione segue modelli basati sui numeri di Fibonacci.
La spirale dei semi di girasole: I semi di girasole sono disposti in spirali che seguono i numeri di Fibonacci.
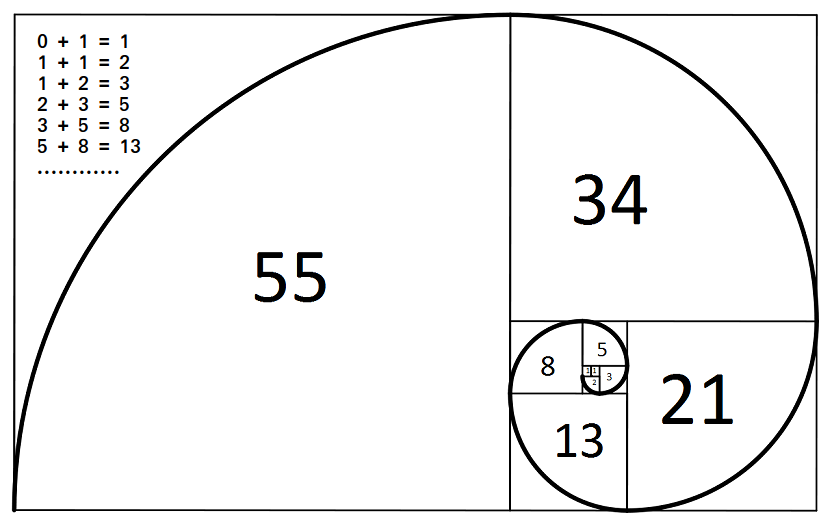
Le spirali delle conchiglie: Molte conchiglie, come il nautilus, presentano una forma a spirale che si approssima alla spirale aurea, derivata dal Rapporto Aureo.
I petali dei fiori: Molti fiori hanno un numero di petali che corrisponde a un numero di Fibonacci (ad esempio, gigli con 3 petali, ranuncoli con 5 petali, ecc.).

Questa presenza ubiquitaria in natura suggerisce che i numeri di Fibonacci riflettono principi fondamentali di crescita e ottimizzazione.

La Serie di Fibonacci nell'Arte e nell'Architettura

Oltre alla natura, la Serie di Fibonacci e il Rapporto Aureo sono stati utilizzati anche nell'arte e nell'architettura per creare composizioni esteticamente piacevoli. Alcuni esempi includono:

Il Partenone: Si ritiene che le proporzioni del Partenone siano basate sul Rapporto Aureo.
Opere d'arte rinascimentali: Molti artisti rinascimentali, come Leonardo da Vinci, hanno utilizzato il Rapporto Aureo nelle loro opere per creare equilibrio e armonia. La Gioconda è un esempio spesso citato.
Musica: Alcuni compositori hanno utilizzato la Serie di Fibonacci per strutturare le loro composizioni.

L'uso del Rapporto Aureo nell'arte e nell'architettura suggerisce che le proporzioni derivate dalla Serie di Fibonacci sono intrinsecamente piacevoli all'occhio umano.

Applicazioni Pratiche della Serie di Fibonacci

Oltre alla bellezza teorica e alle manifestazioni naturali, la Serie di Fibonacci ha anche applicazioni pratiche in diversi campi:

Finanza: Gli analisti tecnici utilizzano i numeri di Fibonacci per identificare potenziali livelli di supporto e resistenza nei mercati finanziari.
Informatica: La Serie di Fibonacci è utilizzata in alcuni algoritmi e strutture dati.
Ottimizzazione: I numeri di Fibonacci possono essere utilizzati per ottimizzare problemi di ricerca e allocazione delle risorse.

Queste applicazioni dimostrano che la Serie di Fibonacci non è solo una curiosità matematica, ma uno strumento utile in diversi contesti.

Sfide e Limiti

Nonostante la sua bellezza e le sue applicazioni, è importante riconoscere anche i limiti della Serie di Fibonacci. Ad esempio:

Interpretazione eccessiva: È facile vedere la Serie di Fibonacci ovunque, anche dove non c'è. È importante essere critici e non forzare l'interpretazione.
Approssimazioni: Le manifestazioni naturali della Serie di Fibonacci sono spesso approssimazioni, non corrispondenze esatte.
Spiegazioni alternative: In alcuni casi, potrebbero esserci spiegazioni alternative più semplici per i fenomeni che sembrano seguire i numeri di Fibonacci.

È fondamentale mantenere un approccio scientifico e non lasciarsi trasportare da interpretazioni eccessivamente romantiche.

Conclusione

La Serie di Fibonacci è molto più di una semplice sequenza di numeri. È un ponte tra la matematica, la natura, l'arte e la finanza. I primi 100 numeri di Fibonacci, con la loro rapida crescita e la loro stretta relazione con il Rapporto Aureo, offrono uno sguardo affascinante sulla bellezza e l'armonia che si celano nel mondo che ci circonda. Speriamo che questo articolo ti abbia ispirato a guardare il mondo con occhi nuovi, alla ricerca dei modelli e delle sequenze che lo governano. Continua ad esplorare, a fare domande e a nutrire la tua curiosità matematica!

Se vuoi approfondire l'argomento, ti consigliamo di consultare le seguenti risorse: