Seno E Coseno Di Un Angolo

Ammettiamolo, chi non ha mai sudato freddo di fronte a seno e coseno? Genitori che cercano di aiutare i figli con i compiti, studenti che fissano il libro senza capirci nulla, insegnanti che si domandano come rendere più accessibile questo argomento apparentemente ostico... Tutti, a un certo punto, ci siamo scontrati con la trigonometria. Ma non temete! Questo articolo è qui per trasformare quel terrore in un'amichevole comprensione. Dimenticate le formule astratte e preparatevi a un viaggio pratico e illuminante nel mondo di seno e coseno.
Cos'è Seno e Coseno? Una Definizione Chiara e Semplice
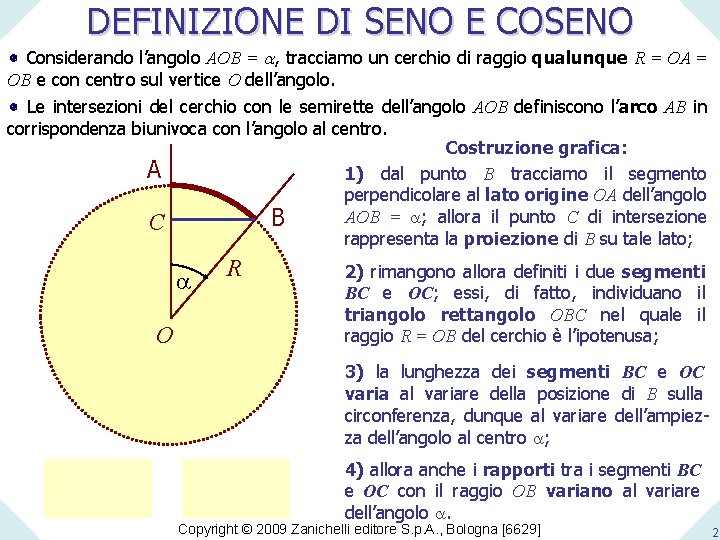
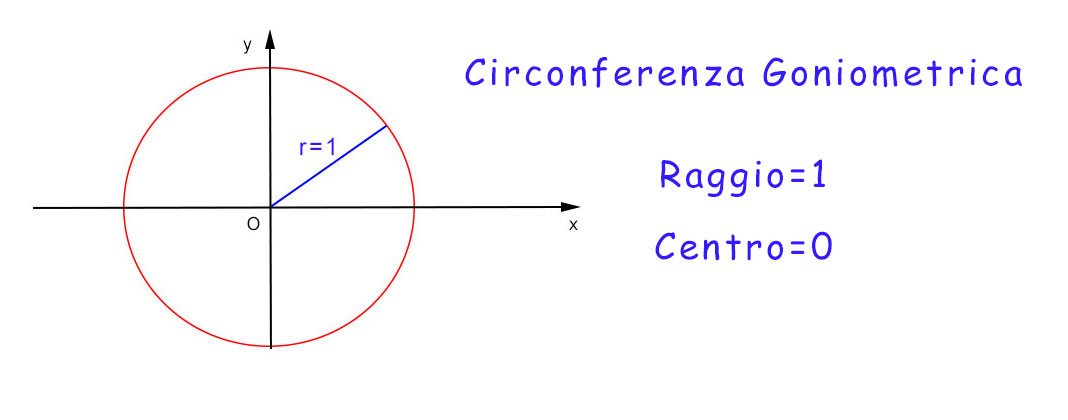
Prima di addentrarci nei dettagli, cerchiamo di capire cosa sono esattamente seno e coseno. Immaginate un cerchio goniometrico, ovvero un cerchio con raggio pari a 1, centrato nell'origine di un sistema di coordinate cartesiane. Ora, prendete un punto qualsiasi su questo cerchio e tracciate una retta che lo congiunge all'origine. L'angolo che questa retta forma con l'asse orizzontale (l'asse delle ascisse) è l'angolo di cui stiamo parlando.
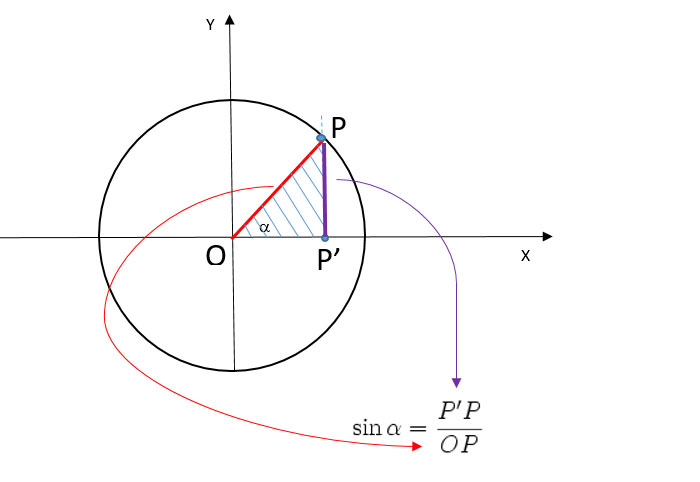
A questo punto, tracciamo una linea verticale dal punto sul cerchio fino all'asse orizzontale. La lunghezza di questa linea verticale rappresenta il seno dell'angolo. Allo stesso modo, la distanza tra l'origine del cerchio e il punto in cui la linea verticale interseca l'asse orizzontale rappresenta il coseno dell'angolo.
In altre parole:
- Seno (sin θ): L'ordinata (valore sull'asse y) del punto sul cerchio goniometrico.
- Coseno (cos θ): L'ascissa (valore sull'asse x) del punto sul cerchio goniometrico.
È fondamentale visualizzare questa immagine del cerchio goniometrico. Vi aiuterà a capire come variano seno e coseno al variare dell'angolo.
Ma perché si chiamano seno e coseno?
L'etimologia di queste parole è affascinante. La parola "seno" deriva da una traduzione errata dall'arabo al latino. In origine, la parola araba "jiba" (corda di un arco) venne confusa con "jaib" (seno, tasca). La parola "coseno" deriva da "complementi sinus", ovvero "seno dell'angolo complementare". Ricordate che due angoli sono complementari se la loro somma è 90 gradi.
Seno e Coseno: Un Esempio Pratico
Immaginate di voler calcolare l'altezza di un albero. Non potete arrampicarvi fino in cima, ma potete misurare l'angolo di elevazione dal suolo e la distanza dalla base dell'albero. Questo è un tipico problema di trigonometria che si risolve utilizzando seno e coseno (e, più precisamente, la tangente, che è il rapporto tra seno e coseno).
Supponiamo che l'angolo di elevazione sia di 30 gradi e la distanza dalla base dell'albero sia di 10 metri. Possiamo usare la tangente per trovare l'altezza:
tan(30°) = altezza / distanza
altezza = tan(30°) * distanza
altezza = (√3 / 3) * 10 metri ≈ 5.77 metri
Quindi, l'altezza dell'albero è approssimativamente di 5.77 metri. Questo è solo un esempio di come seno e coseno vengono utilizzati per risolvere problemi reali.
Le Proprietà Fondamentali di Seno e Coseno
Seno e coseno non sono solo definizioni, ma anche funzioni con proprietà specifiche. Vediamo le più importanti:
- Periodicità: Sia seno che coseno sono funzioni periodiche con un periodo di 2π (360 gradi). Questo significa che il loro valore si ripete ogni 2π radianti. Matematicamente, sin(θ + 2π) = sin(θ) e cos(θ + 2π) = cos(θ).
- Valori Massimi e Minimi: Sia seno che coseno hanno valori compresi tra -1 e 1. Il valore massimo è 1 e il valore minimo è -1. Questo è facilmente visualizzabile sul cerchio goniometrico: l'ordinata e l'ascissa del punto non possono mai essere maggiori di 1 o minori di -1.
- Simmetria: Il coseno è una funzione pari, il che significa che cos(-θ) = cos(θ). Graficamente, questo significa che il grafico del coseno è simmetrico rispetto all'asse y. Il seno è una funzione dispari, il che significa che sin(-θ) = -sin(θ). Graficamente, questo significa che il grafico del seno è simmetrico rispetto all'origine.
- Relazione Fondamentale: Esiste una relazione fondamentale tra seno e coseno, nota come identità trigonometrica fondamentale: sin²(θ) + cos²(θ) = 1. Questa identità deriva direttamente dal teorema di Pitagora applicato al triangolo rettangolo formato dal raggio del cerchio goniometrico, l'ordinata e l'ascissa del punto.
Comprendere queste proprietà è cruciale per manipolare le funzioni trigonometriche e risolvere equazioni.
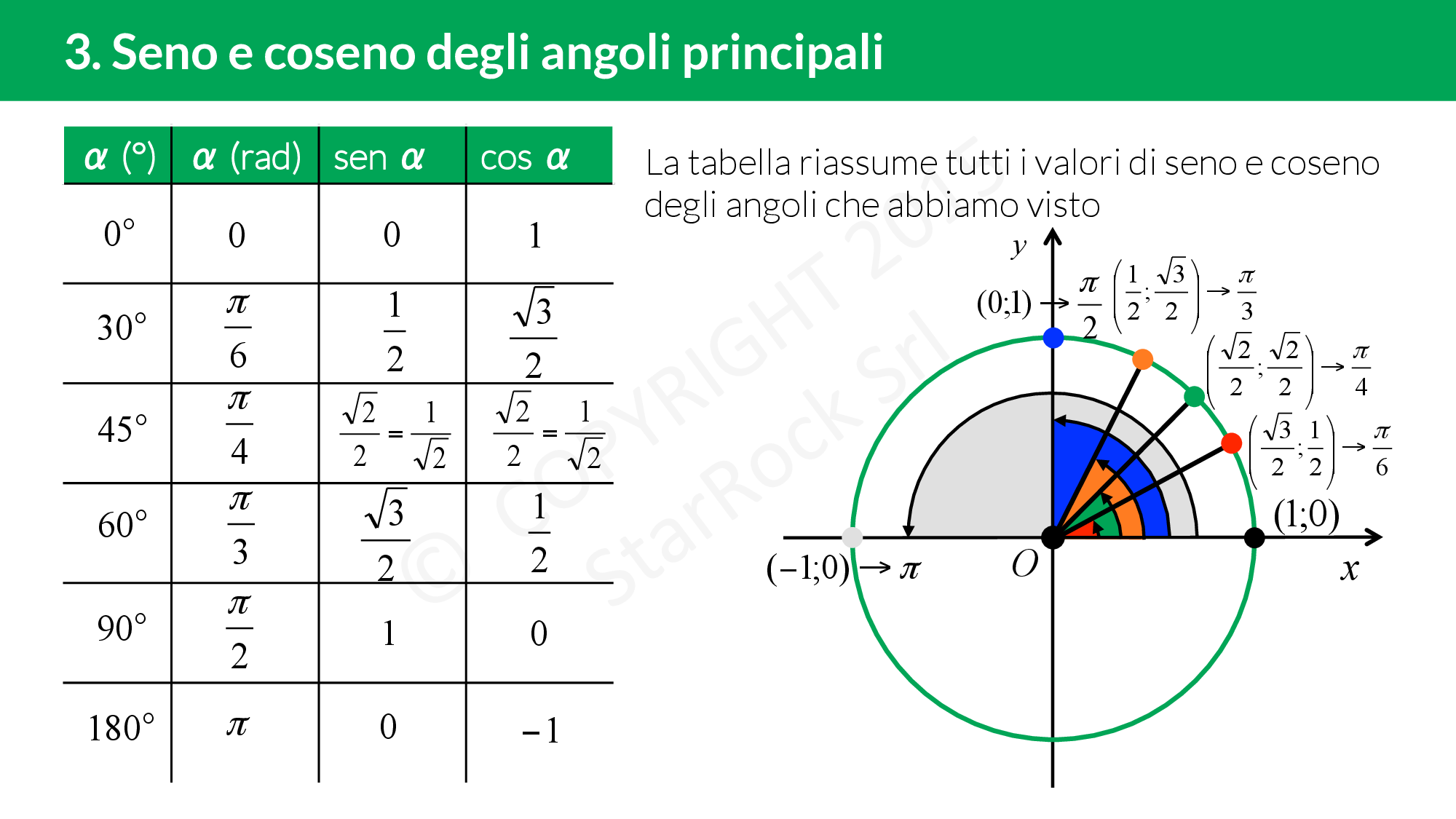
Seno e Coseno: Valori Notevoli e la Tabella Trigonometrica
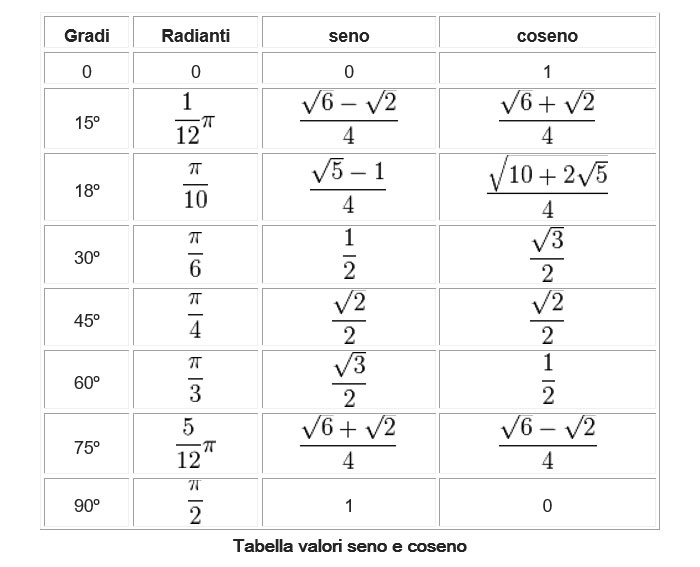
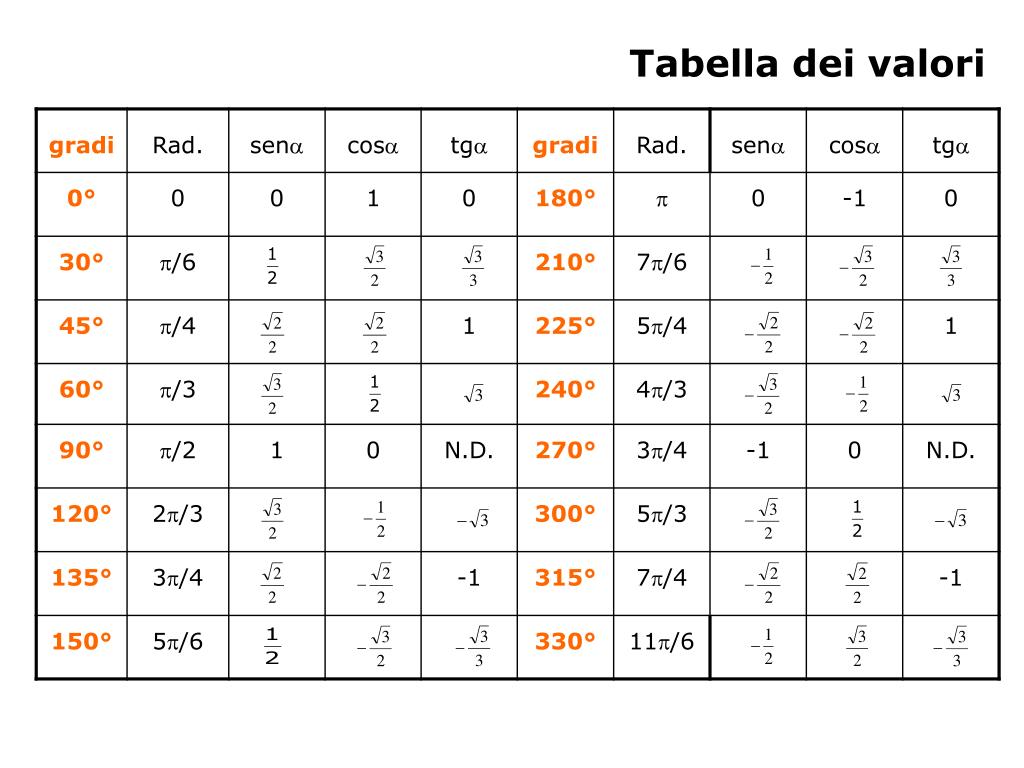
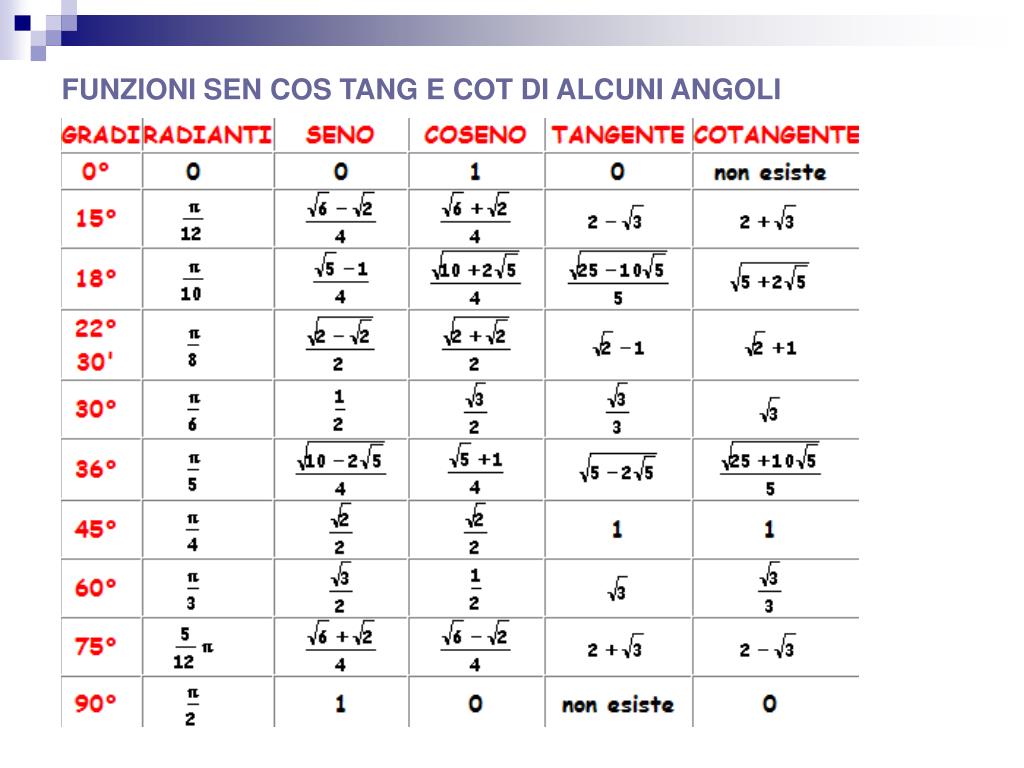
Ci sono alcuni angoli i cui valori di seno e coseno sono particolarmente importanti e vengono spesso utilizzati. Questi angoli sono 0, 30, 45, 60 e 90 gradi (o 0, π/6, π/4, π/3 e π/2 radianti).
Ecco una tabella con i valori di seno e coseno per questi angoli:
| Angolo (gradi) | Angolo (radianti) | sin(θ) | cos(θ) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 30 | π/6 | 1/2 | √3/2 |
| 45 | π/4 | √2/2 | √2/2 |
| 60 | π/3 | √3/2 | 1/2 |
| 90 | π/2 | 1 | 0 |
È molto utile memorizzare questi valori o almeno capire come ricavarli. Possono essere utilizzati per risolvere rapidamente molti problemi trigonometrici.
Esercizi Pratici: Mettiamoci alla Prova
La teoria è importante, ma la pratica è fondamentale per padroneggiare seno e coseno. Ecco alcuni esercizi per mettere alla prova la vostra comprensione:
- Calcolare sin(150°) e cos(150°). Suggerimento: usate le proprietà di simmetria e periodicità.
- Un aereo vola ad un'altitudine di 1000 metri. L'angolo di depressione (l'angolo tra l'orizzontale e la linea di vista verso il basso) di un aeroporto è di 20 gradi. Qual è la distanza orizzontale tra l'aereo e l'aeroporto?
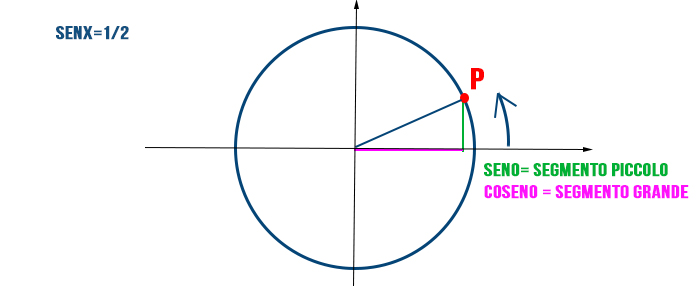
- Risolvere l'equazione sin(x) = 0.5 per x compreso tra 0 e 2π.
Provate a risolvere questi esercizi. Se avete difficoltà, rileggete l'articolo e cercate di capire il ragionamento alla base di ogni passaggio. La chiave è la comprensione concettuale, non la memorizzazione meccanica.
Seno e Coseno: Oltre la Trigonometria
Seno e coseno non sono solo concetti astratti confinati alla trigonometria. Hanno applicazioni in una vasta gamma di campi, tra cui:
- Fisica: Descrizione di onde, oscillazioni, moto armonico semplice.
- Ingegneria: Analisi di circuiti elettrici, progettazione di ponti e strutture.
- Informatica: Grafica computerizzata, elaborazione del segnale.
- Musica: Analisi del suono, sintesi musicale.
Capire seno e coseno vi aprirà le porte a un mondo di applicazioni pratiche e teoriche.
In conclusione, seno e coseno possono sembrare spaventosi all'inizio, ma con una comprensione chiara dei concetti fondamentali, delle proprietà e delle applicazioni, possono diventare strumenti potenti e affascinanti. Non abbiate paura di sperimentare, di fare domande e di mettere in pratica ciò che avete imparato. La matematica, come la vita, è un viaggio continuo di scoperta e apprendimento.