Scomposizione Con Il Metodo Di Ruffini

Capita a tutti, prima o poi, di trovarsi di fronte a un polinomio apparentemente indecifrabile e di pensare: "Da dove inizio?". La scomposizione in fattori, soprattutto quando si incontrano polinomi di grado superiore al secondo, può sembrare un ostacolo insormontabile. Ma non temere! Esistono metodi, come quello di Ruffini, che ci permettono di affrontare queste sfide con metodo e sicurezza.

Questo articolo è pensato per guidarti passo dopo passo nella comprensione e nell'applicazione del metodo di Ruffini, offrendoti strumenti pratici e un approccio che ti aiuterà a superare le difficoltà e a riscoprire il piacere della matematica.

Cos'è la Scomposizione in Fattori e Perché è Importante?

Prima di immergerci nel metodo di Ruffini, è fondamentale capire cos'è la scomposizione in fattori e perché è così importante. Immagina di avere un numero, ad esempio 12. Possiamo scriverlo come prodotto di altri numeri: 12 = 3 x 4, oppure 12 = 2 x 6, o ancora 12 = 2 x 2 x 3. Questa è la scomposizione in fattori primi.

Allo stesso modo, la scomposizione in fattori di un polinomio significa scriverlo come prodotto di polinomi di grado inferiore. Ad esempio, il polinomio x² - 4 può essere scomposto in (x - 2)(x + 2).

Ma perché è così importante? La scomposizione in fattori è una tecnica fondamentale in algebra per diverse ragioni:

Semplificazione di espressioni algebriche: Permette di ridurre espressioni complesse a forme più semplici, facilitando i calcoli.
Risoluzione di equazioni: Aiuta a trovare le soluzioni (o radici) di un'equazione polinomiale.
Analisi di funzioni: Fornisce informazioni preziose sul comportamento di una funzione, come i suoi zeri e i suoi punti di intersezione con gli assi.

In sostanza, la scomposizione in fattori è uno strumento potente che ci permette di comprendere e manipolare le espressioni algebriche in modo più efficace.

Il Metodo di Ruffini: Un Approccio Passo Passo

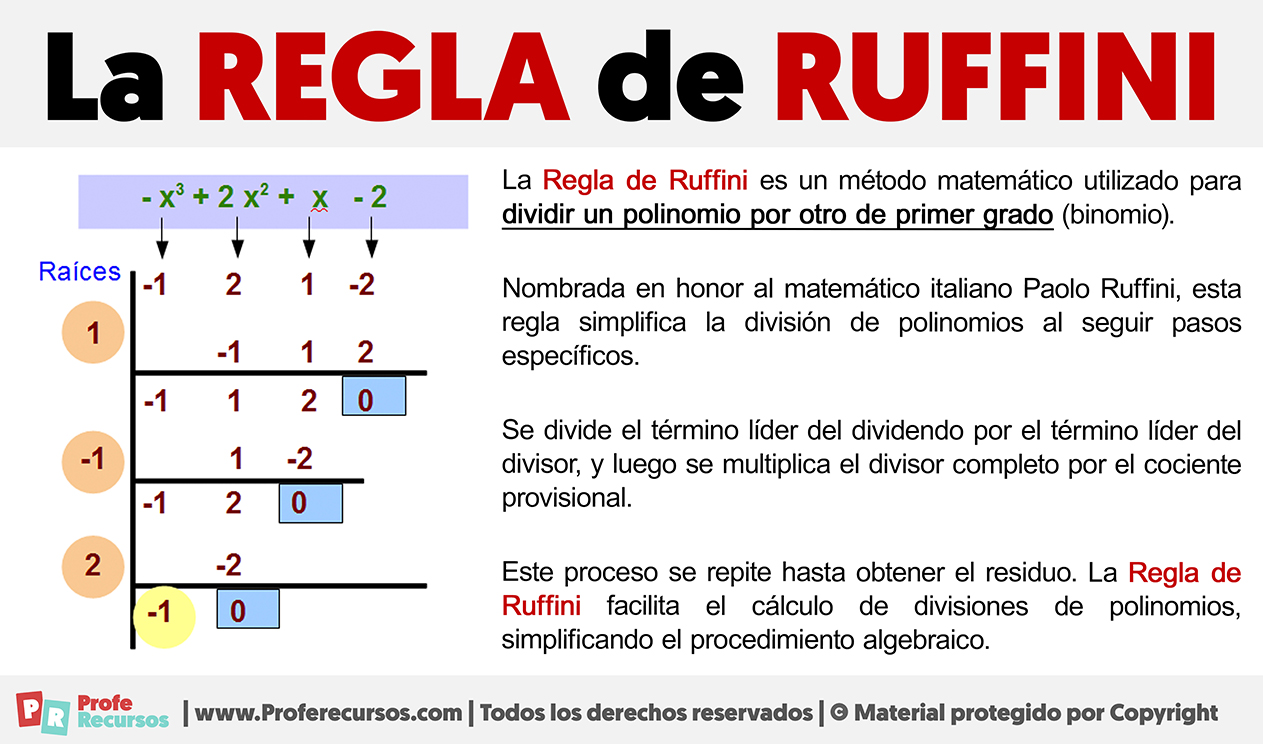
Il metodo di Ruffini è un algoritmo che permette di dividere un polinomio per un binomio della forma (x - a). Il risultato della divisione è un quoziente e un resto. Se il resto è zero, significa che (x - a) è un fattore del polinomio, e quindi abbiamo trovato una scomposizione!

Ecco i passi da seguire:

Individuare i divisori del termine noto: Il termine noto è il termine senza la variabile x (es. in x³ + 2x² - 5x - 6, il termine noto è -6). I divisori del termine noto sono i numeri che lo dividono esattamente (es. i divisori di -6 sono ±1, ±2, ±3, ±6). Questi saranno i nostri candidati per "a" nel binomio (x - a).
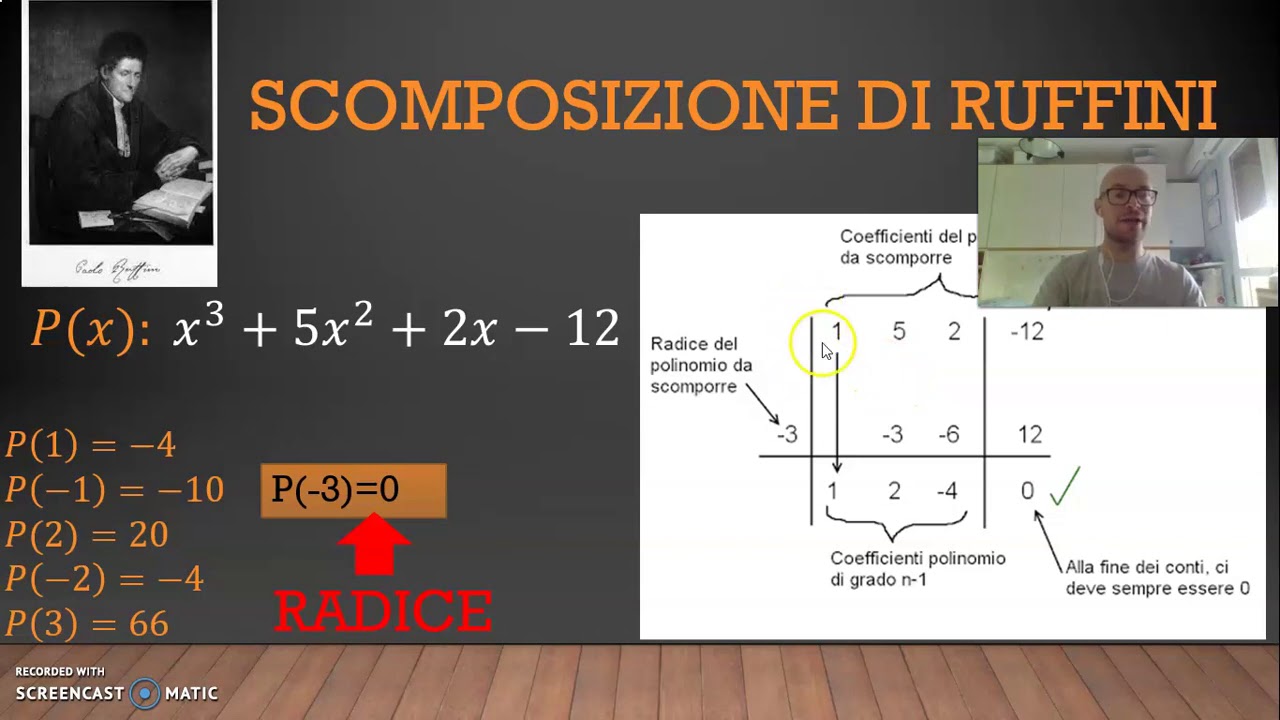
Costruire la tabella di Ruffini: Disegna una tabella come quella che vedi spesso negli esempi. Nella prima riga, scrivi i coefficienti del polinomio, assicurandoti che siano in ordine decrescente di grado e che non manchi nessun termine (se manca un termine, inserisci uno 0). A sinistra della tabella, scrivi uno dei divisori del termine noto che hai individuato al punto 1.
Eseguire l'algoritmo:
- Abbassa il primo coefficiente.
- Moltiplica il coefficiente abbassato per il divisore che hai scritto a sinistra.
- Scrivi il risultato sotto il secondo coefficiente e somma.
- Ripeti i passi 2 e 3 fino a raggiungere l'ultimo coefficiente.
Interpretare i risultati: L'ultimo numero che ottieni è il resto della divisione. Se il resto è 0, significa che il divisore che hai scelto è una radice del polinomio e che (x - a) è un fattore del polinomio. Gli altri numeri nella tabella sono i coefficienti del polinomio quoziente.

Esempio Pratico: Scomponiamo il polinomio P(x) = x³ + 2x² - 5x - 6

1. Divisori del termine noto (-6): ±1, ±2, ±3, ±6

2. Proviamo con x = -1 (cioè a = -1, quindi il binomio è (x + 1)):

-1 | 1   2  -5  -6
   |    -1  -1   6
   ----------------
   | 1   1  -6   0

3. Interpretazione: Il resto è 0, quindi (x + 1) è un fattore del polinomio. Il polinomio quoziente è x² + x - 6.

4. Conclusione: Abbiamo scomposto il polinomio in P(x) = (x + 1)(x² + x - 6). Ora possiamo scomporre ulteriormente il polinomio di secondo grado (x² + x - 6) usando altri metodi, come il trinomio speciale o la formula risolutiva per le equazioni di secondo grado.

Consigli Utili per l'Applicazione del Metodo

Inizia con i divisori più semplici: Solitamente, provare con ±1 e ±2 può portare a risultati più velocemente.
Non arrenderti al primo tentativo: Se il resto non è zero, prova con un altro divisore.
Verifica sempre il risultato: Moltiplica i fattori che hai trovato per assicurarti di ottenere il polinomio originale.
Sii ordinato: Scrivi i passaggi in modo chiaro e ordinato per evitare errori di calcolo.
Utilizza la calcolatrice: Per i calcoli più complessi, non esitare a usare la calcolatrice.

Superare le Difficoltà Comuni

È normale incontrare difficoltà quando si impara un nuovo metodo. Ecco alcuni problemi comuni e come superarli:

Confusione con i segni: Presta molta attenzione ai segni dei coefficienti e dei divisori. Un errore di segno può compromettere l'intero calcolo.
Difficoltà a individuare i divisori: Se hai difficoltà a trovare i divisori del termine noto, puoi usare un metodo sistematico, come la scomposizione in fattori primi del termine noto.
Errori di calcolo: Controlla attentamente i tuoi calcoli, soprattutto le moltiplicazioni e le somme.
Blocchi mentali: Se ti senti bloccato, fai una pausa, respira profondamente e prova a rivedere i passaggi con calma. Chiedi aiuto a un compagno di classe, al tuo insegnante o a un tutor.

Ricorda che la pratica rende perfetti. Più esercizi farai, più diventerai bravo nell'applicazione del metodo di Ruffini. Non scoraggiarti di fronte alle difficoltà, ma considera ogni errore come un'opportunità per imparare e migliorare.

Il Ruolo dell'Insegnante e dei Genitori

L'insegnante e i genitori possono svolgere un ruolo fondamentale nel supportare gli studenti nell'apprendimento del metodo di Ruffini.

Suggerimenti per gli Insegnanti:

Spiega il metodo in modo chiaro e graduale: Usa esempi concreti e semplici per introdurre il metodo.
Fornisci esercizi di difficoltà crescente: Inizia con esercizi semplici e poi aumenta gradualmente la difficoltà.
Incoraggia gli studenti a lavorare in gruppo: Il lavoro di gruppo può favorire la comprensione e la risoluzione dei problemi.
Offri feedback costruttivo: Aiuta gli studenti a identificare i loro errori e a correggerli.
Utilizza strumenti visivi: Tabelle, diagrammi e altri strumenti visivi possono rendere il metodo più comprensibile.
Collega il metodo a situazioni reali: Mostra agli studenti come la scomposizione in fattori può essere utile in contesti pratici.

Suggerimenti per i Genitori:

Crea un ambiente di apprendimento positivo: Incoraggia tuo figlio a fare domande e a esprimere le sue difficoltà.
Offri il tuo aiuto: Se ti senti a tuo agio, aiuta tuo figlio a svolgere i compiti. In caso contrario, considera la possibilità di ingaggiare un tutor.
Sii paziente e comprensivo: Ricorda che l'apprendimento richiede tempo e impegno.
Celebra i successi: Riconosci e celebra i progressi di tuo figlio, anche se piccoli.
Comunica con l'insegnante: Parla con l'insegnante di tuo figlio per capire quali sono le sue difficoltà e come puoi aiutarlo.

Conclusione: La Scomposizione è una Sfida Superabile

La scomposizione in fattori con il metodo di Ruffini può sembrare difficile all'inizio, ma con la giusta guida, la pratica e la perseveranza, chiunque può imparare a padroneggiarla. Ricorda che la matematica è come un viaggio: ci saranno ostacoli lungo il percorso, ma con la giusta preparazione e il giusto atteggiamento, potrai raggiungere la tua meta.

Non aver paura di chiedere aiuto, di fare errori e di ricominciare da capo. Ogni passo che fai ti avvicina alla comprensione e alla padronanza di questo strumento potente. E ricorda: la matematica è ovunque intorno a noi, e imparare a comprenderla significa aprire le porte a un mondo di possibilità.