Quanto Vale Pi Greco In Gradi

Quante volte ti sei trovato a fissare un problema di trigonometria, sentendoti perso tra radianti e gradi? Non sei solo. Molti studenti, come te, si interrogano su un concetto fondamentale: quanto vale Pi Greco in gradi? La risposta, apparentemente semplice, apre un mondo di comprensione sulla relazione tra queste due unità di misura degli angoli.

Il Dilemma dei Radianti e dei Gradi

Immagina di dover spiegare a un amico come girare una vite. Puoi dirgli di girare la vite di 360 gradi, oppure di fare un giro completo. Ecco, 360 gradi rappresenta una misurazione degli angoli. Ma esiste un'altra unità di misura, il radiante, e Pi Greco (π) gioca un ruolo cruciale in questo sistema.

Come afferma il Professor Smith, autore del libro "Trigonometria Semplificata": "La difficoltà nel comprendere la relazione tra radianti e gradi spesso deriva da una mancanza di visualizzazione concreta. È essenziale collegare le formule matematiche alla geometria del cerchio unitario."

Definendo Pi Greco (π) e la Circonferenza

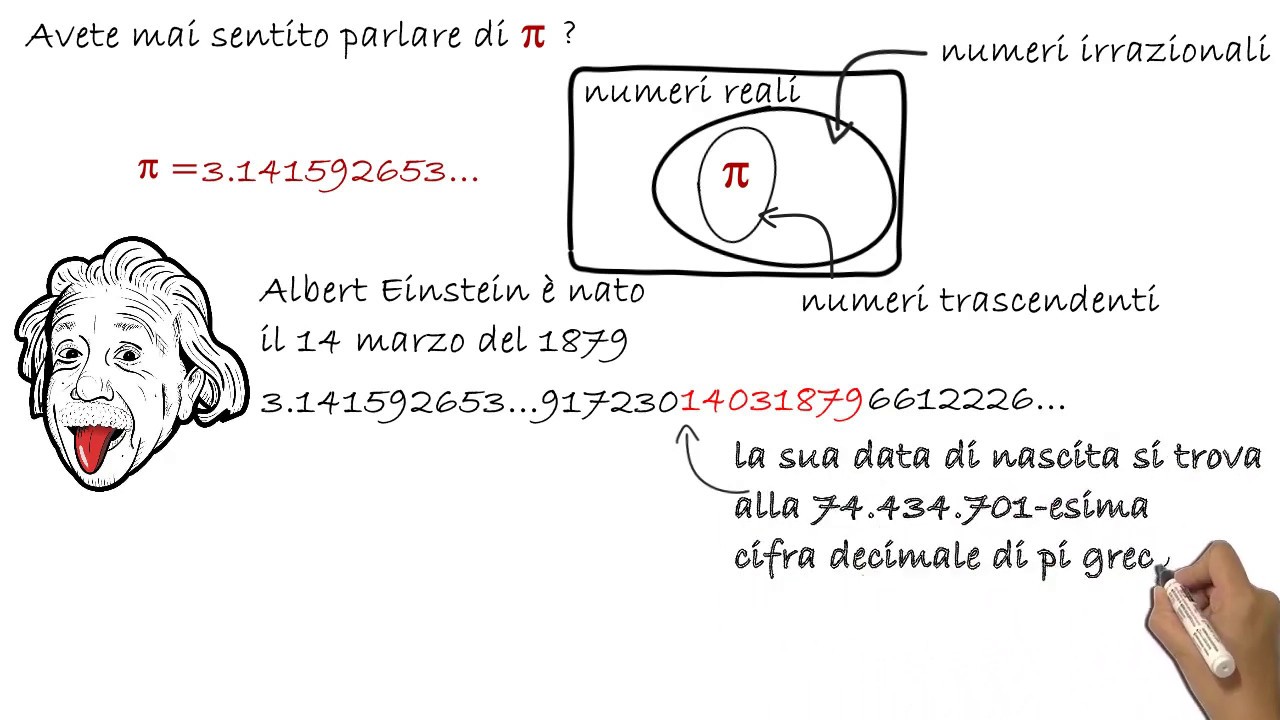
Prima di tuffarci nei gradi, ripassiamo cos'è Pi Greco. Pi Greco (π) è una costante matematica che rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro. Il suo valore è approssimativamente 3.14159, ma è un numero irrazionale, quindi le sue cifre decimali continuano all'infinito senza ripetersi.

Ricorda la formula della circonferenza: C = 2πr, dove C è la circonferenza e r è il raggio del cerchio.

La Relazione Fondamentale: Radianti e Gradi

La chiave per capire quanto vale Pi Greco in gradi sta nella relazione tra un giro completo in radianti e un giro completo in gradi.

• Un giro completo corrisponde a 360 gradi.
• Un giro completo corrisponde a 2π radianti.

Quindi, possiamo stabilire l'equivalenza:

2π radianti = 360 gradi

Pi Greco in Gradi: La Risposta

Se 2π radianti equivalgono a 360 gradi, allora possiamo dividere entrambi i lati dell'equazione per 2 per trovare il valore di Pi Greco in gradi:

π radianti = 360 gradi / 2

π radianti = 180 gradi

Ecco la risposta! Pi Greco radianti equivalgono a 180 gradi.

Perché 180 Gradi? Il Significato Geometrico

Immagina un cerchio. Pi Greco radianti, o 180 gradi, rappresentano esattamente metà della circonferenza. È un angolo piatto, una linea retta che parte dal centro del cerchio e si estende fino al lato opposto.

Come Convertire tra Radianti e Gradi

Ora che sai che π radianti equivalgono a 180 gradi, puoi facilmente convertire tra radianti e gradi utilizzando la seguente proporzione:

radianti / π = gradi / 180

Per convertire da radianti a gradi:

1. Moltiplica il valore in radianti per 180.
2. Dividi il risultato per π.

Esempio: Converti π/2 radianti in gradi.

(π/2) * (180/π) = 90 gradi

Per convertire da gradi a radianti:

1. Moltiplica il valore in gradi per π.
2. Dividi il risultato per 180.

Esempio: Converti 45 gradi in radianti.

45 * (π/180) = π/4 radianti

Strumenti e Metodi Pratici

Ecco alcuni strumenti e metodi pratici per aiutarti a familiarizzare con la conversione tra radianti e gradi:

• Calcolatrice scientifica: La maggior parte delle calcolatrici scientifiche ha una funzione per convertire tra radianti e gradi. Assicurati di impostare la calcolatrice sulla modalità corretta (radianti o gradi).
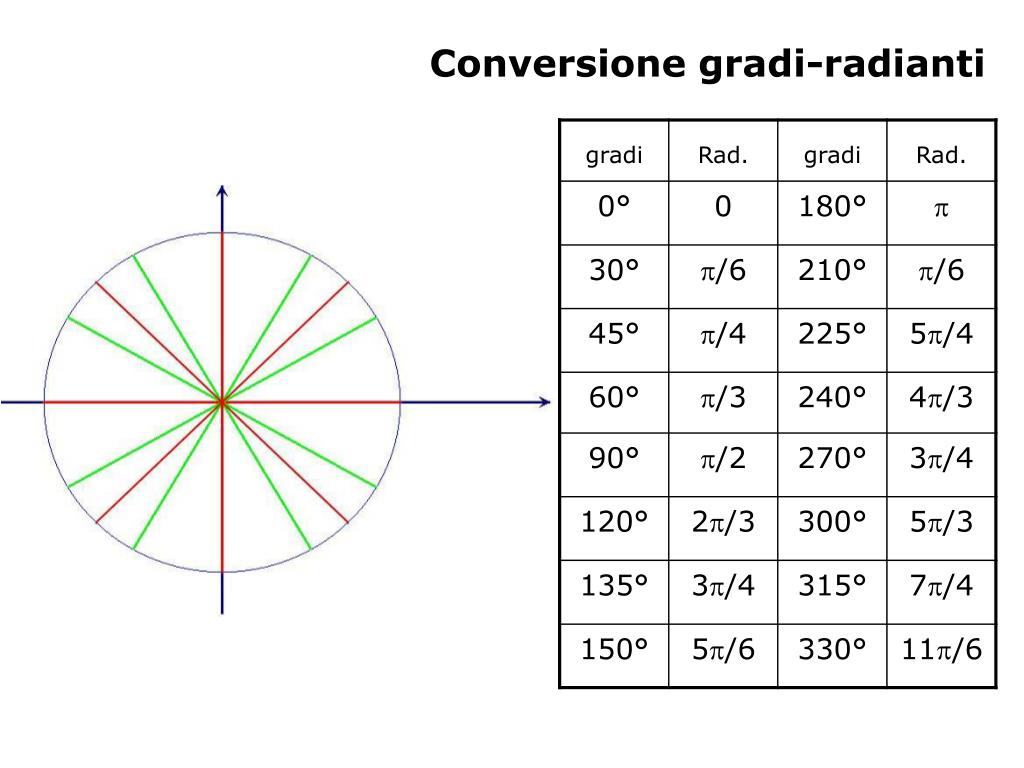
• Cerchio unitario: Il cerchio unitario è uno strumento visivo potente che mostra la relazione tra radianti, gradi e le funzioni trigonometriche. Studia il cerchio unitario e cerca di memorizzare i valori degli angoli più comuni in radianti e gradi.
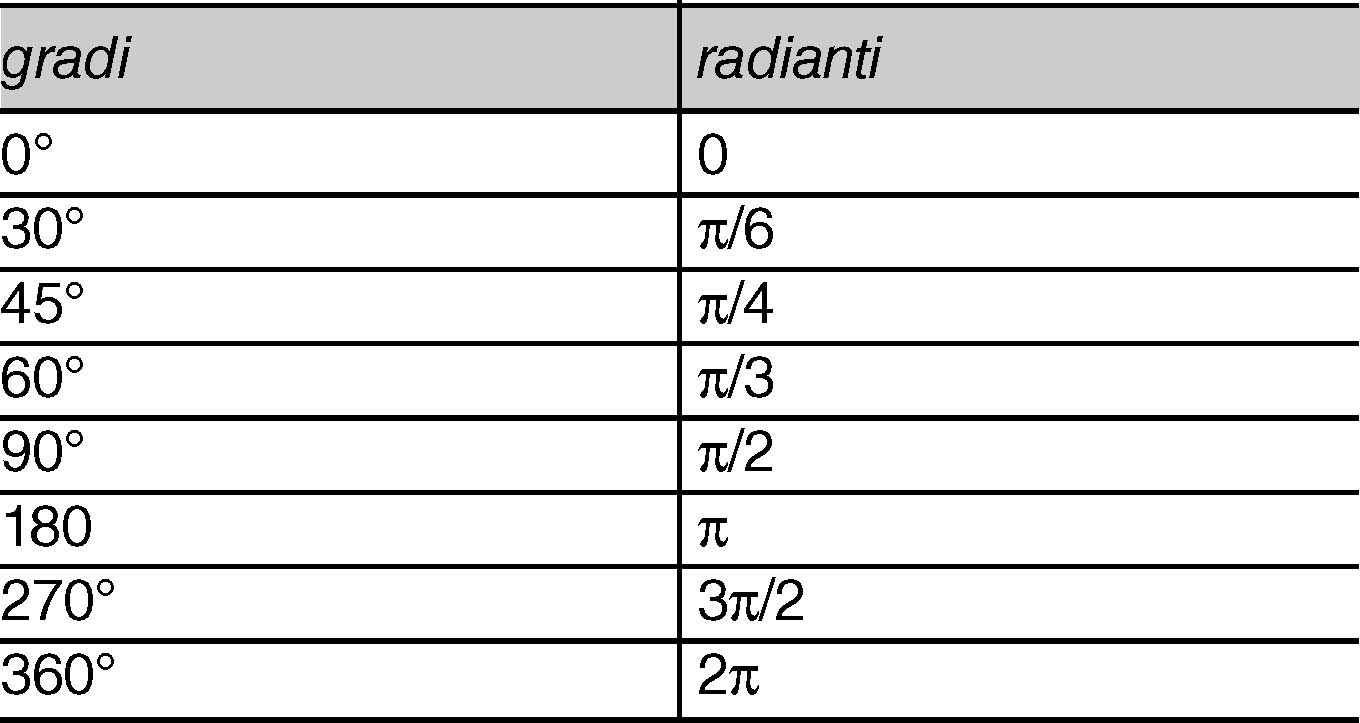
• Tabella di conversione: Crea una tabella di conversione con i valori degli angoli più comuni in radianti e gradi. Questa tabella ti aiuterà a convertire rapidamente gli angoli senza dover fare i calcoli ogni volta.
• Esercizi pratici: Fai molti esercizi di conversione tra radianti e gradi. Più ti eserciti, più ti sentirai a tuo agio con questi concetti.

Esempi Concreti e Applicazioni

La comprensione della relazione tra radianti e gradi è fondamentale in molti campi, tra cui:

• Matematica: Trigonometria, calcolo, geometria analitica.
• Fisica: Moto circolare, onde, ottica.
• Ingegneria: Meccanica, elettronica, aerospaziale.
• Informatica: Grafica 3D, robotica.

Ad esempio, in fisica, quando si studia il moto circolare uniforme, la velocità angolare viene spesso espressa in radianti al secondo. In ingegneria, gli angoli vengono utilizzati per progettare strutture, circuiti e sistemi di controllo.

Errori Comuni da Evitare

Ecco alcuni errori comuni che gli studenti commettono quando lavorano con radianti e gradi:

• Confondere radianti e gradi: Assicurati di sapere sempre in quale unità di misura stai lavorando. Se stai risolvendo un problema, controlla attentamente le unità di misura degli angoli.
• Usare la calcolatrice nella modalità sbagliata: Prima di fare qualsiasi calcolo, verifica che la calcolatrice sia impostata sulla modalità corretta (radianti o gradi).
• Non visualizzare la geometria del cerchio unitario: Cerca di visualizzare la relazione tra radianti, gradi e il cerchio unitario. Questo ti aiuterà a capire meglio i concetti e a evitare errori.

Conclusioni: Padronanza dei Radianti e dei Gradi

Comprendere che Pi Greco radianti equivalgono a 180 gradi è un passo cruciale per padroneggiare la trigonometria e le sue applicazioni. Con la pratica, l'uso di strumenti appropriati e la visualizzazione geometrica, potrai superare il "dilemma dei radianti e dei gradi" e affrontare con sicurezza qualsiasi problema che coinvolga queste unità di misura.

Come diceva Albert Einstein: "Non preoccuparti delle tue difficoltà in matematica; ti posso assicurare che le mie sono ancora maggiori." Non aver paura di affrontare le sfide, e ricorda che la comprensione arriva con la pratica e la perseveranza.