Quando Una Funzione Non è Derivabile

Cara studentessa, caro studente,

Nel viaggio affascinante e a volte tortuoso attraverso il mondo della matematica, incontriamo concetti che ci sfidano, che ci chiedono di guardare oltre la superficie. Uno di questi concetti è quello della non derivabilità di una funzione. Potrebbe sembrare un ostacolo, una limitazione, ma in realtà, è un’opportunità straordinaria per crescere, per affinare la nostra comprensione e per sviluppare qualità essenziali per la vita, non solo per lo studio.

Immagina una funzione come un sentiero che si snoda attraverso un paesaggio. La derivata, in un certo punto, è come la pendenza del sentiero in quel preciso istante. Ci dice quanto rapidamente stiamo salendo o scendendo. Ma cosa succede se il sentiero improvvisamente si interrompe, diventa spigoloso, o si divide in due direzioni diverse?

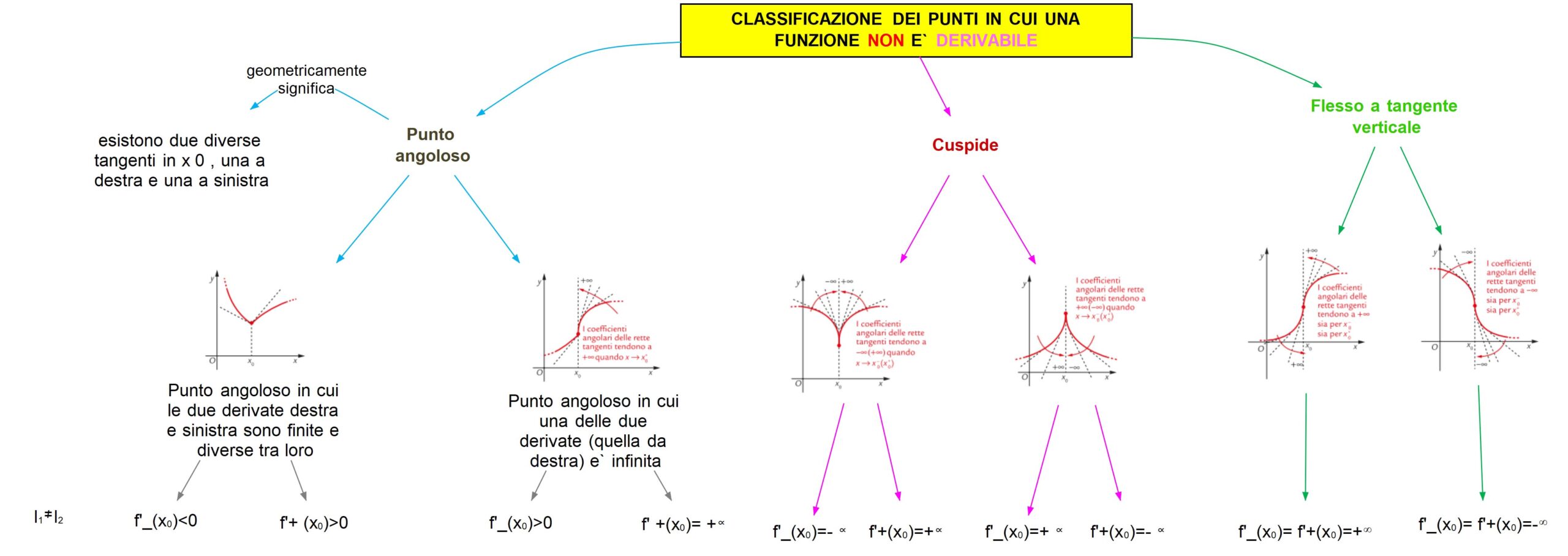
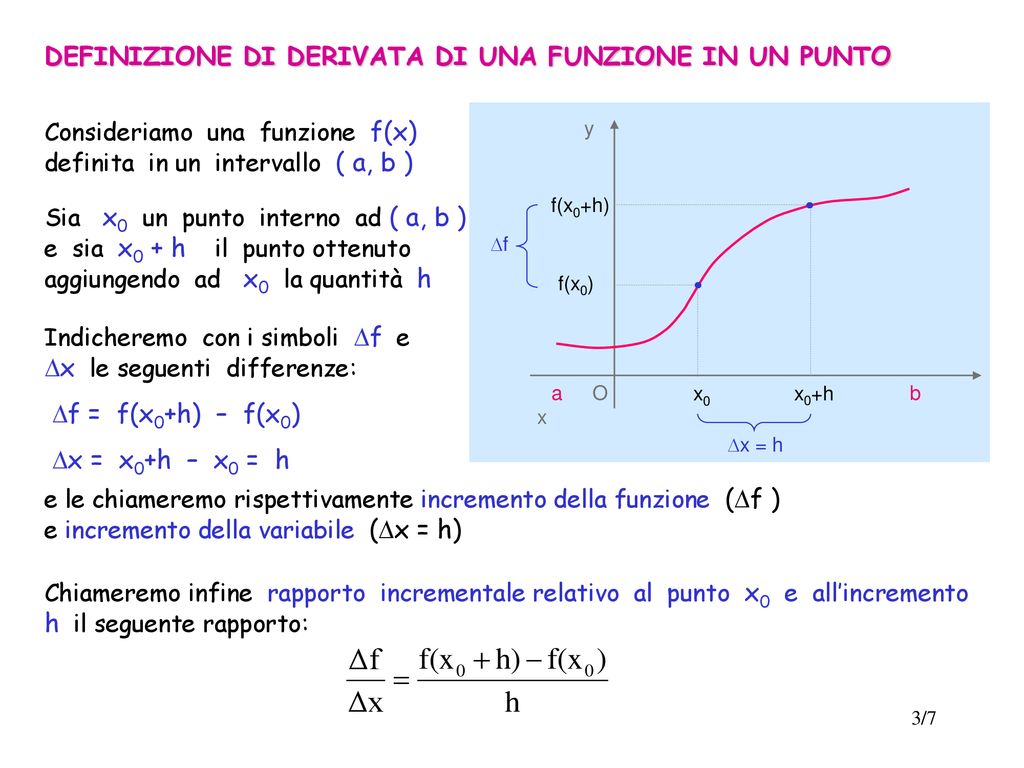
È proprio qui che entra in gioco la non derivabilità. Una funzione non è derivabile in un punto se, per usare un linguaggio più formale, il limite del rapporto incrementale non esiste in quel punto. Tradotto in termini più semplici, significa che la "pendenza" in quel punto non è ben definita. Può essere infinitamente ripida, oppure presentare un salto brusco, o magari due "pendenze" diverse a seconda della direzione da cui ci avviciniamo.

Cosa ci insegna questo?

Innanzitutto, ci insegna l'importanza della curiosità. Invece di sentirci frustrati di fronte a un punto di non derivabilità, possiamo chiederci: "Perché succede questo? Cosa c'è di particolare in questo punto?" Questa domanda apre la porta a un'esplorazione più profonda, a una comprensione più ricca della funzione e del suo comportamento.

In secondo luogo, ci insegna l'umiltà. La matematica, come la vita, è piena di sorprese. A volte le cose non vanno come ci aspettiamo. Accettare che una funzione possa non essere derivabile non è un segno di debolezza, ma di maturità intellettuale. Riconoscere i limiti del nostro modello, del nostro approccio, è fondamentale per imparare e crescere.

"L'ignoranza è la madre della sorpresa." - Proverbio

In terzo luogo, ci insegna la perseveranza. Capire la non derivabilità richiede spesso un po' di impegno. Dobbiamo studiare il comportamento della funzione in prossimità del punto critico, analizzare i limiti da destra e da sinistra, magari utilizzare strumenti grafici per visualizzare la situazione. Ma ogni sforzo profuso ci ripaga con una comprensione più solida e duratura.

Esempi pratici

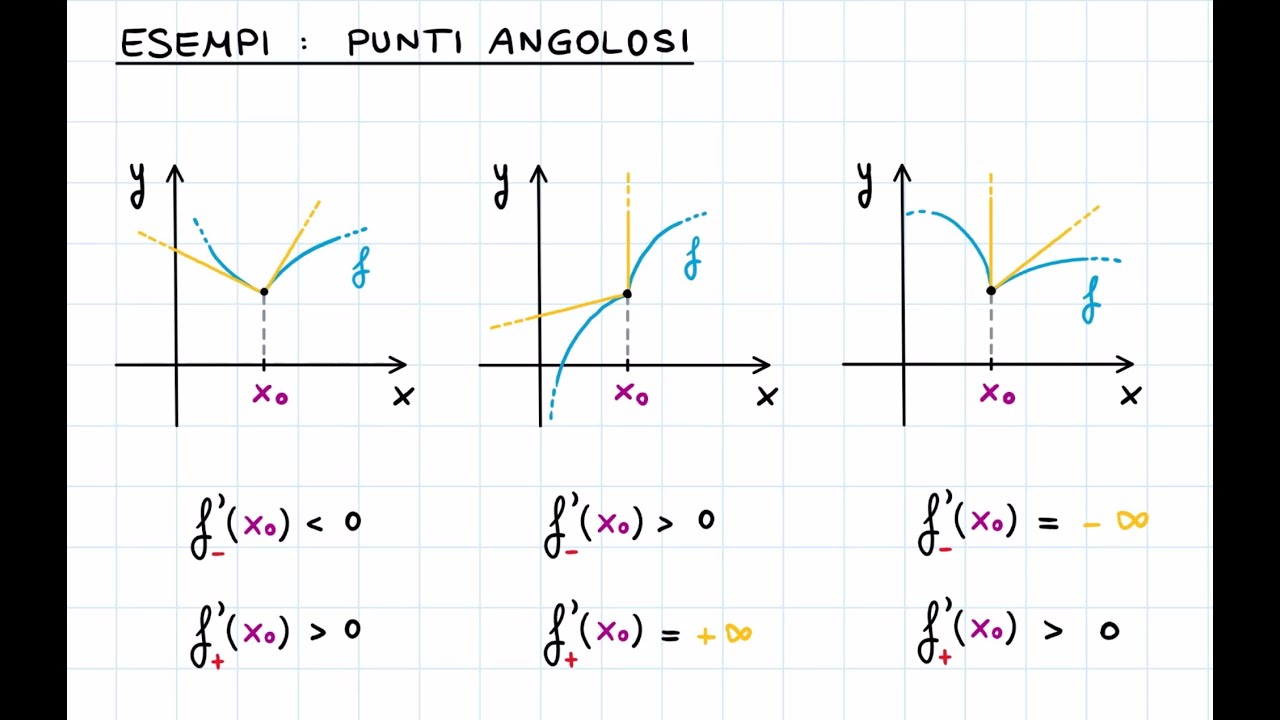
Pensa al valore assoluto di x, |x|. È una funzione continua, ma nel punto x = 0 presenta un "angolo". La derivata da sinistra è -1, mentre la derivata da destra è +1. Quindi, in x = 0 la funzione non è derivabile. Questo ci ricorda che la continuità non implica necessariamente la derivabilità.

Un altro esempio è una funzione definita a tratti, dove le diverse espressioni si "incontrano" in un punto. Se le derivate delle due espressioni non coincidono in quel punto, la funzione non sarà derivabile in quel punto.

Questi esempi, e molti altri, ci mostrano che la non derivabilità è un fenomeno comune, un aspetto intrinseco della natura delle funzioni. Invece di evitarlo, impariamo ad abbracciarlo, a studiarlo, a comprenderlo.

La matematica è molto più che una serie di formule e regole. È un modo di pensare, un modo di affrontare i problemi, un modo di imparare dalla realtà. La non derivabilità di una funzione è una piccola, ma significativa, lezione di vita. Ci insegna che non tutto è liscio e prevedibile, che a volte dobbiamo fare i conti con l'imprevisto, con l'irregolarità, con la discontinuità. Ma è proprio in queste "imperfezioni" che si nasconde la bellezza e la ricchezza della matematica, e della vita.

Continua a esplorare, a domandare, a imparare. Il mondo della matematica è vasto e meraviglioso, e la tua curiosità è la chiave per svelarne i segreti. Ricorda, l'importante non è arrivare sempre alla risposta giusta, ma il viaggio che fai per raggiungerla.

In bocca al lupo per il tuo studio!