Quando Due Rette Si Dicono Complanari

Ti sei mai trovato a lavorare con figure nello spazio, magari in un progetto di design 3D o semplicemente cercando di visualizzare un concetto geometrico, e ti sei chiesto se due linee, apparentemente intrecciate, appartengono allo stesso "foglio" invisibile, lo stesso piano? Capire quando due rette sono complanari è fondamentale in molte discipline, dalla geometria all'ingegneria, e può semplificare notevolmente la risoluzione di problemi complessi.

Questo articolo ti guiderà attraverso il concetto di complanarità tra rette, fornendoti una comprensione chiara e pratica, indipendentemente dal tuo background matematico.

Cosa Significa "Complanare"?

La parola "complanare" deriva dal latino "complanus", che significa "sullo stesso piano". In geometria, due o più elementi (punti, rette, segmenti, poligoni) sono detti complanari se giacciono tutti sullo stesso piano. Immagina un foglio di carta: qualsiasi punto o linea disegnata su quel foglio è complanare con il foglio stesso. Due rette sono complanari se esiste un piano che le contiene entrambe.

Perché è Importante?

Determinare la complanarità di due rette è cruciale per diversi motivi:

Semplificazione dei problemi: Se sappiamo che due rette sono complanari, possiamo lavorare con la geometria piana anziché con la geometria tridimensionale, semplificando notevolmente i calcoli.
Applicazioni pratiche: In ingegneria civile, ad esempio, la complanarità è essenziale nella progettazione di ponti e strutture, assicurando che gli elementi siano correttamente allineati e che le forze siano distribuite in modo appropriato.
Grafica 3D: Nella grafica computerizzata, la complanarità è fondamentale per la rappresentazione accurata degli oggetti tridimensionali e per evitare artefatti visivi.

Come Stabilire se Due Rette Sono Complanari

Esistono diversi metodi per determinare se due rette sono complanari. Ne esploreremo alcuni dei più comuni, con esempi pratici.

1. Metodo Vettoriale

Questo metodo è particolarmente utile quando le rette sono definite in forma parametrica o vettoriale. Siano r e s le due rette. Se r è definita da un punto A e un vettore direzione u, e s è definita da un punto B e un vettore direzione v, allora le rette sono complanari se e solo se il vettore AB (il vettore che va da A a B) è complanare con i vettori u e v.

In altre parole, il prodotto misto (o prodotto triplo scalare) dei vettori AB, u e v deve essere zero. Ricorda che il prodotto misto è definito come: AB · (u × v), dove "·" rappresenta il prodotto scalare e "×" rappresenta il prodotto vettoriale.

In sintesi: Se AB · (u × v) = 0, allora le rette r e s sono complanari.

Esempio:

Siano le rette r e s definite come segue:

r: x = 1 + t, y = 2 - t, z = 3 + 2t s: x = 4 - s, y = 1 + s, z = 5 + 3s

Da r, prendiamo il punto A(1, 2, 3) e il vettore direzione u = (1, -1, 2). Da s, prendiamo il punto B(4, 1, 5) e il vettore direzione v = (-1, 1, 3).

Il vettore AB è (4-1, 1-2, 5-3) = (3, -1, 2).

Calcoliamo il prodotto vettoriale u × v:

u × v = ( (-1)(3) - (2)(1), (2)(-1) - (1)(3), (1)(1) - (-1)(-1) ) = (-5, -5, 0)

Calcoliamo il prodotto misto AB · (u × v):

AB · (u × v) = (3)(-5) + (-1)(-5) + (2)(0) = -15 + 5 + 0 = -10

Poiché il prodotto misto è diverso da zero (-10 ≠ 0), le rette r e s non sono complanari. Sono sghembe.

2. Metodo Determinantale

Questo metodo è una formulazione alternativa del metodo vettoriale, espressa in termini di determinante di una matrice. Mantenendo la notazione precedente, formiamo una matrice 3x3 i cui vettori riga sono AB, u e v. Le rette sono complanari se e solo se il determinante di questa matrice è zero.

In sintesi: Le rette sono complanari se:

Utilizzando lo stesso esempio precedente, la matrice sarebbe:

| 3 -1 2 | | 1 -1 2 | | -1 1 3 |

Il determinante di questa matrice è:

3((-1)(3) - (2)(1)) - (-1)((1)(3) - (2)(-1)) + 2((1)(1) - (-1)(-1)) = 3(-5) + 1(5) + 2(0) = -15 + 5 + 0 = -10

Anche in questo caso, il determinante è diverso da zero, confermando che le rette non sono complanari.

3. Metodo delle Equazioni Cartesiane

Se le rette sono espresse in forma cartesiana (come intersezione di due piani), possiamo verificare la complanarità determinando se esiste un piano che contiene entrambe le rette. Questo può essere più complesso e spesso richiede la risoluzione di sistemi di equazioni.

Siano r e s due rette espresse come:

r: a₁x + b₁y + c₁z + d₁ = 0, a₂x + b₂y + c₂z + d₂ = 0 s: a₃x + b₃y + c₃z + d₃ = 0, a₄x + b₄y + c₄z + d₄ = 0

Se esiste una combinazione lineare delle quattro equazioni che si riduce a un'identità (0 = 0), allora le rette sono complanari. In pratica, questo implica risolvere un sistema di equazioni lineari per trovare i coefficienti di tale combinazione lineare.

Cosa Succede se le Rette sono Parallele o Incidenti?

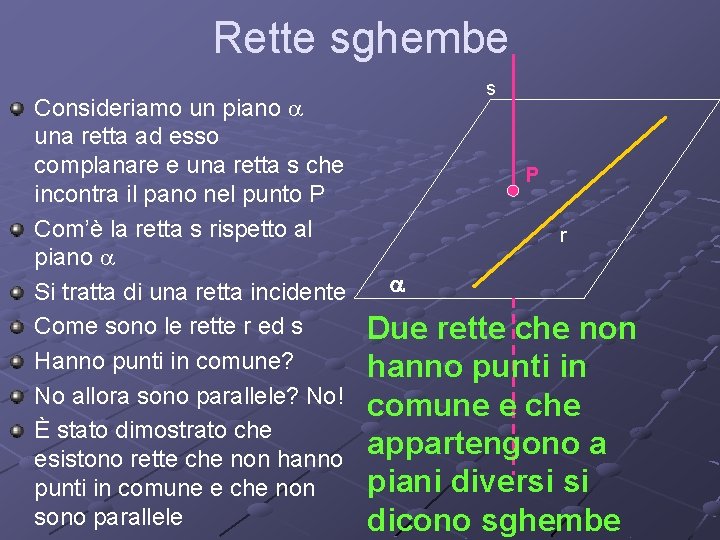
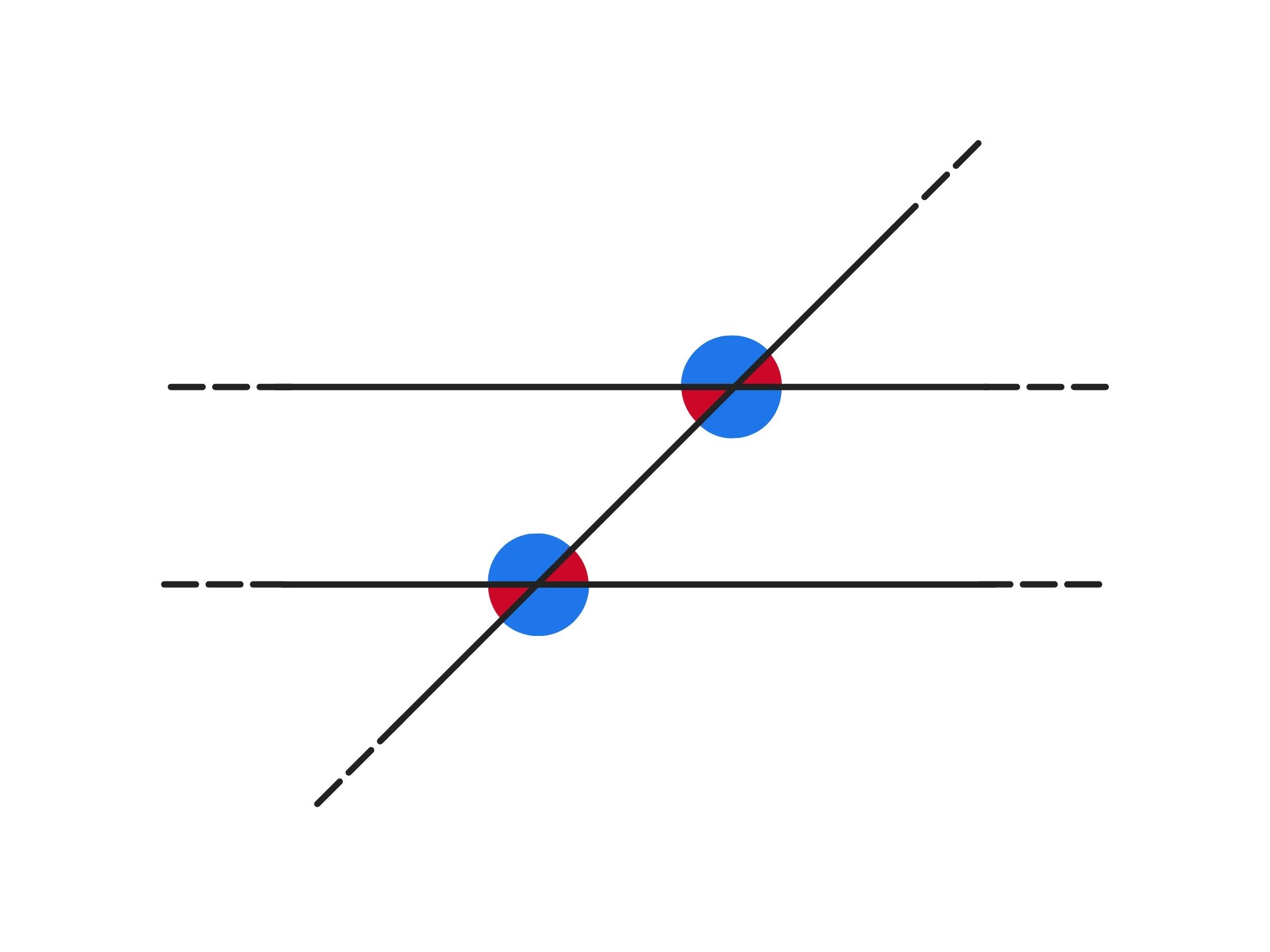
Due rette parallele sono sempre complanari. Per definizione, due rette parallele giacciono sullo stesso piano e non si intersecano mai.

Due rette incidenti (che si intersecano in un punto) sono anche sempre complanari. Il punto di intersezione definisce un piano unico che contiene entrambe le rette.

La difficoltà sorge quando le rette sono sghembe, ovvero non sono parallele e non si intersecano. In questo caso, non sono complanari.

Esempi Pratici

Esempio 1: Progettazione di un Ponte

Un ingegnere deve progettare un ponte sospeso. Due cavi portanti devono essere posizionati in modo tale da essere complanari per garantire una distribuzione uniforme del carico. L'ingegnere utilizza il metodo vettoriale per verificare la complanarità dei cavi, assicurandosi che il prodotto misto dei vettori di posizione e direzione sia zero.

Esempio 2: Grafica 3D

Un game developer deve creare un modello 3D di una spada. Due spigoli della lama devono essere complanari per rendere la superficie liscia e realistica. Il developer utilizza un software di modellazione 3D che calcola automaticamente il determinante della matrice formata dai vettori che definiscono gli spigoli. Se il determinante è prossimo allo zero (tenendo conto della tolleranza numerica), gli spigoli sono considerati complanari.

Consigli Utili

Visualizza il problema: Prima di iniziare i calcoli, cerca di visualizzare la situazione nello spazio. Disegnare un diagramma può aiutarti a comprendere meglio la geometria del problema.
Scegli il metodo giusto: Il metodo migliore dipende dalla forma in cui sono date le equazioni delle rette. Il metodo vettoriale è spesso il più semplice se le rette sono in forma parametrica.
Verifica i risultati: Dopo aver calcolato la complanarità, verifica sempre i tuoi risultati. Se possibile, utilizza un software di calcolo simbolico o un calcolatore online per controllare i tuoi calcoli.

Conclusioni

Comprendere il concetto di complanarità tra rette è essenziale per risolvere problemi in una vasta gamma di discipline. Abbiamo esplorato diversi metodi per determinare se due rette sono complanari, dal metodo vettoriale al metodo determinantale, e abbiamo visto come applicare questi concetti in situazioni pratiche. Speriamo che questo articolo ti abbia fornito una solida base per affrontare problemi di geometria nello spazio con maggiore sicurezza e competenza.