Quando Due Angoli Si Dicono Adiacenti

Ti sei mai fermato a osservare come le figure geometriche interagiscono tra loro? In particolare, gli angoli, che sono la base di molte costruzioni e forme che ci circondano, possono avere relazioni speciali. Forse stai studiando geometria a scuola e ti senti un po' confuso da tutti questi termini. Oppure, sei semplicemente curioso di capire meglio il mondo che ti circonda, dal modo in cui sono costruiti gli edifici alla disposizione dei mobili in casa. In entrambi i casi, questo articolo ti aiuterà a comprendere in modo chiaro e semplice cosa significa quando due angoli si dicono adiacenti.

Cosa sono gli angoli adiacenti? Una definizione chiara

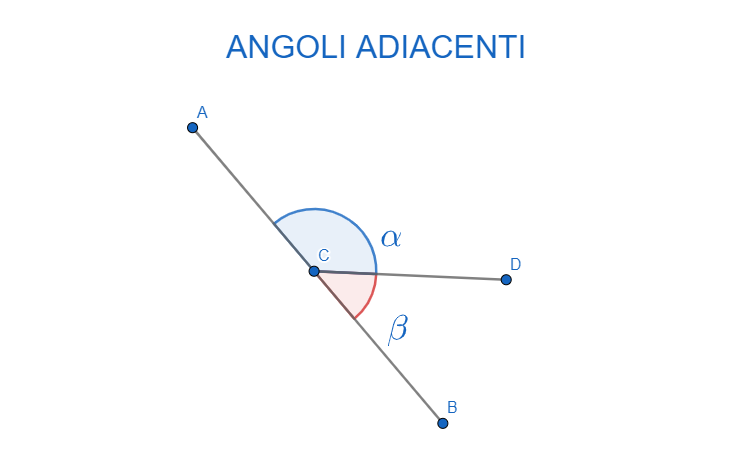
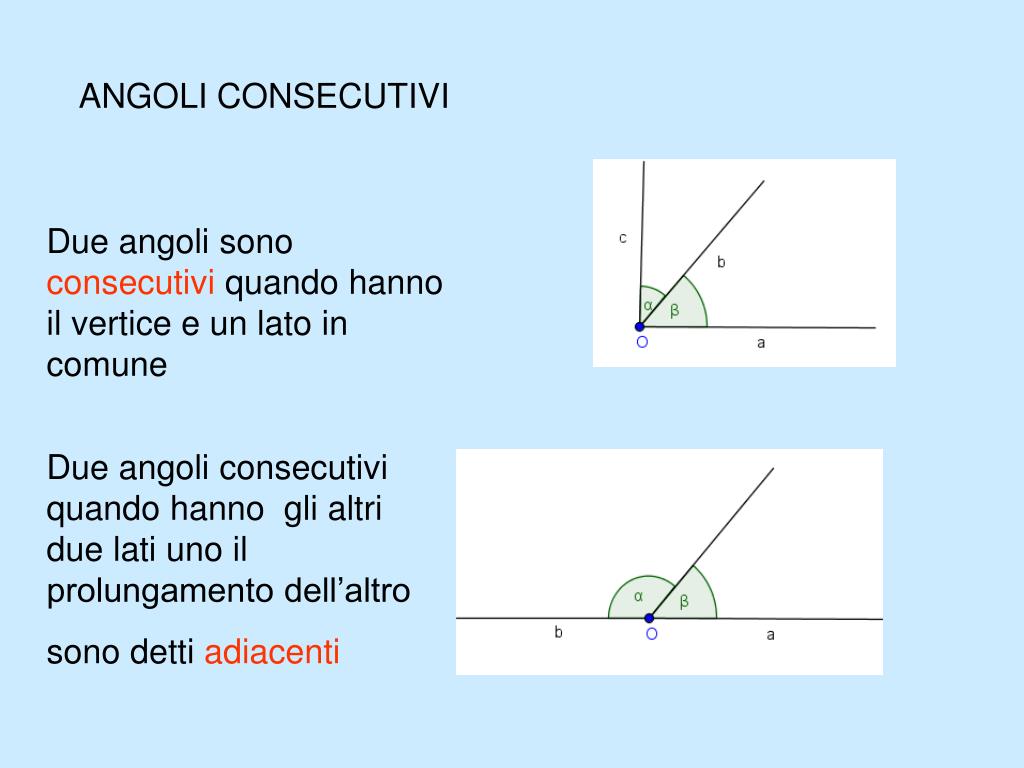
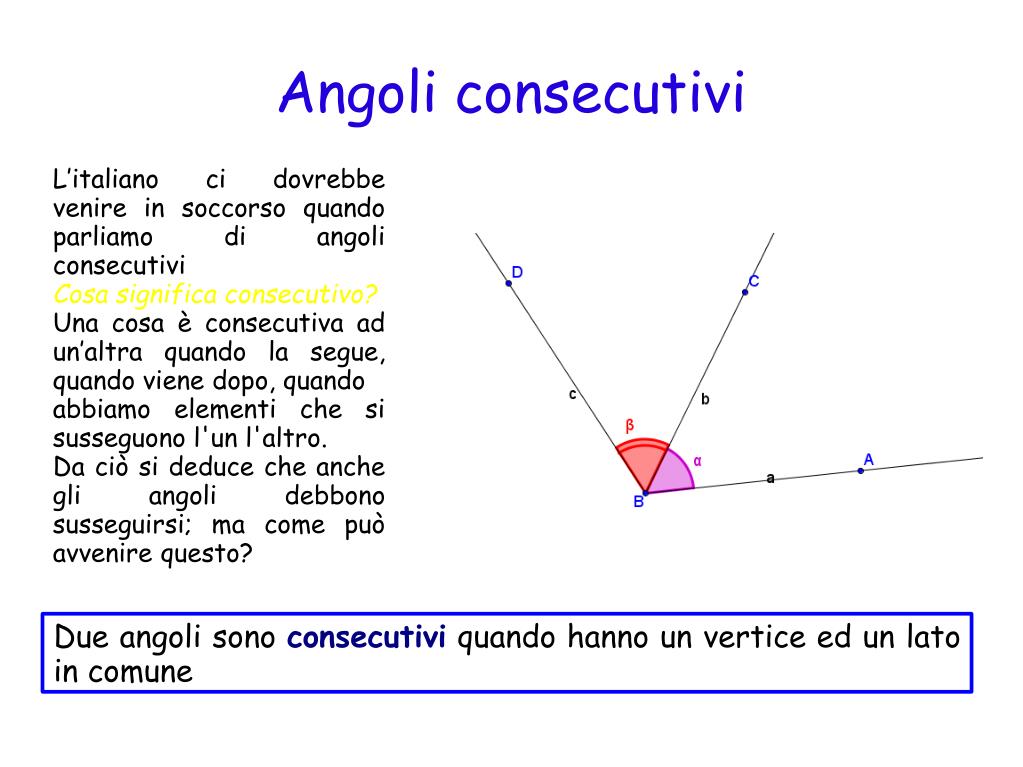
Due angoli sono definiti adiacenti se soddisfano contemporaneamente le seguenti tre condizioni:

Condividono un vertice: Hanno lo stesso punto di origine. Immagina due strade che si incontrano in un incrocio; quell'incrocio è il vertice.
Condividono un lato: Hanno un lato in comune. Pensa a due fette di torta tagliate dallo stesso punto centrale; il taglio tra le due fette è il lato in comune.
Non hanno punti interni in comune: Non si sovrappongono. Se sovrapponessero, non sarebbero più "vicini" ma "sovrapposti".

In parole più semplici, due angoli adiacenti sono "vicini" l'uno all'altro, condividono un "muro" (il lato in comune) e non si "invadono" a vicenda (non hanno punti interni in comune). Pensa a due case vicine; condividono il muro di confine (il lato in comune) e sono costruite sullo stesso terreno (hanno lo stesso vertice nel piano geometrico), ma non si sovrappongono.

Un esempio pratico: le lancette dell'orologio

Visualizzare la definizione può essere utile. Immagina un orologio analogico. Prendi in considerazione l'angolo formato dalla lancetta delle ore e la lancetta dei minuti, e l'angolo formato dalla lancetta dei minuti e il numero 12. Questi due angoli *possono* essere adiacenti, a seconda della posizione delle lancette. Se la lancetta dei minuti è posizionata esattamente sul numero 12, allora l'angolo tra le ore e i minuti *non* è adiacente all'angolo tra i minuti e il numero 12, perché non hanno punti interni in comune; sono praticamente lo stesso angolo. Se, invece, la lancetta dei minuti è posizionata tra il numero 12 e il numero 1, allora i due angoli sono adiacenti: condividono il vertice (il centro dell'orologio), condividono un lato (la lancetta dei minuti) e non si sovrappongono.

Perché è importante conoscere gli angoli adiacenti? Applicazioni reali

La conoscenza degli angoli adiacenti non è solo un esercizio teorico. Ha applicazioni pratiche in diversi campi:

Architettura e Ingegneria: Gli architetti e gli ingegneri utilizzano i concetti di angoli adiacenti per progettare edifici, ponti e altre strutture. La stabilità e la resistenza di una struttura dipendono in gran parte dall'angolo con cui i diversi elementi si incontrano. Ad esempio, la corretta angolazione delle travi di un tetto, spesso formando angoli adiacenti, è fondamentale per distribuire il peso in modo uniforme e prevenire crolli.
Design d'interni: Quando disponiamo i mobili in una stanza, spesso creiamo angoli adiacenti, anche senza rendercene conto. Ad esempio, l'angolo formato da due divani posti uno di fronte all'altro, condividendo un lato del tappeto come vertice, può influenzare la percezione dello spazio e il flusso della conversazione.
Grafica computerizzata e videogiochi: Gli angoli adiacenti sono fondamentali per la modellazione 3D e l'animazione. I modelli 3D sono costruiti da poligoni, che a loro volta sono definiti da angoli. La corretta definizione degli angoli adiacenti garantisce che i modelli abbiano un aspetto realistico e si comportino correttamente nell'ambiente virtuale.
Navigazione: La navigazione, sia terrestre che marittima, utilizza concetti geometrici che includono angoli adiacenti per determinare la posizione e la direzione. Ad esempio, la triangolazione, una tecnica utilizzata per determinare la posizione di un punto sulla superficie terrestre, si basa sulla misurazione di angoli adiacenti.

Un esempio più specifico: la costruzione di una casa

Immagina di costruire una casa. Le pareti si incontrano formando angoli. Quando due pareti si uniscono in un angolo e non si sovrappongono, condividendo il vertice (l'angolo della stanza) e il lato (la linea di giunzione tra le pareti), formano angoli adiacenti. La comprensione di questo concetto è fondamentale per garantire che le pareti siano allineate correttamente e che la struttura sia stabile.

Cosa succede se non rispettiamo le condizioni di adiacenza?

Se due angoli non soddisfano tutte e tre le condizioni di adiacenza, allora *non* sono adiacenti. Potrebbero essere:

Sovrapposti: Come detto prima, se hanno punti interni in comune.
Opposti al vertice: Angoli formati da due rette che si intersecano. Questi angoli sono uguali, ma non adiacenti.
Complementari: Due angoli la cui somma è 90 gradi. Possono essere adiacenti o meno.
Supplementari: Due angoli la cui somma è 180 gradi. Possono essere adiacenti o meno.
Semplicemente non correlati: Angoli che non condividono né vertice, né lato, e quindi non hanno alcuna relazione specifica.

Controindicazioni: errori comuni e come evitarli

Un errore comune è confondere gli angoli adiacenti con gli angoli complementari o supplementari. Ricorda, gli angoli adiacenti devono *condividere* un lato e un vertice, mentre gli angoli complementari e supplementari si riferiscono solo alla *somma* delle loro misure. Un altro errore è non considerare la condizione che gli angoli non debbano avere punti interni in comune. Due angoli che condividono un vertice e un lato, ma si sovrappongono, *non* sono adiacenti.

Per evitare questi errori, è utile visualizzare gli angoli su un diagramma. Disegna gli angoli, evidenzia il vertice e il lato in comune, e verifica se si sovrappongono. La pratica rende perfetti!

Un'altra prospettiva: il ruolo del linguaggio

Anche il linguaggio può trarre in inganno. La parola "adiacente" implica "vicinanza", ma in geometria la vicinanza non è sufficiente. Gli angoli devono rispettare le tre condizioni specificate. Pensa alla parola "parallelo". Intuitivamente, pensiamo a due rette che vanno nella stessa direzione. Ma la definizione precisa è: due rette che giacciono sullo stesso piano e non si intersecano mai. La precisione è fondamentale in geometria.

Soluzioni e approcci pratici

Ecco alcuni suggerimenti per comprendere meglio gli angoli adiacenti:

Utilizza strumenti visivi: Disegna angoli su carta o utilizza software di geometria dinamica per esplorare diverse configurazioni.
Esercitati con esempi: Risolvi esercizi che richiedono di identificare angoli adiacenti in diverse figure geometriche.
Spiega il concetto ad altri: Insegnare è il modo migliore per imparare. Cerca di spiegare il concetto di angoli adiacenti a un amico o a un familiare.
Collega il concetto alla vita reale: Cerca esempi di angoli adiacenti nel mondo che ti circonda, come negli edifici, nei mobili o negli oggetti di uso quotidiano.

Ricorda, la geometria è come un linguaggio: richiede pratica e dedizione per essere padroneggiata. Non scoraggiarti se all'inizio trovi difficoltà. Con il tempo e l'impegno, diventerai sempre più sicuro e competente.

Riflessioni finali e prossimi passi

Comprendere il concetto di angoli adiacenti è un passo fondamentale nello studio della geometria. Questo concetto apparentemente semplice è alla base di molte costruzioni e principi più complessi. Prenditi un momento per riflettere su come questo concetto si applica al mondo che ti circonda. Osserva gli angoli formati dagli oggetti nella tua stanza, dalle strade che percorri, dagli edifici che ammiri. Cerca di identificare gli angoli adiacenti e di applicare la definizione che abbiamo discusso.

Ora che hai una solida comprensione degli angoli adiacenti, sei pronto per esplorare concetti geometrici più avanzati. Forse potresti approfondire lo studio degli angoli complementari e supplementari, o esplorare le proprietà dei triangoli e dei poligoni. Qualunque sia il tuo prossimo passo, ricorda che la chiave del successo è la curiosità, la pratica e la perseveranza.

Quali esempi di angoli adiacenti riesci a trovare nella tua vita quotidiana?