Qual è Lo Spigolo Di Un Cubo
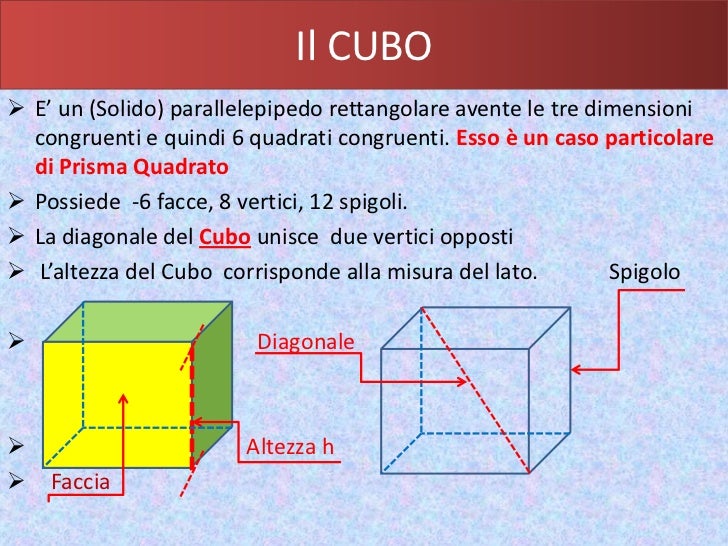
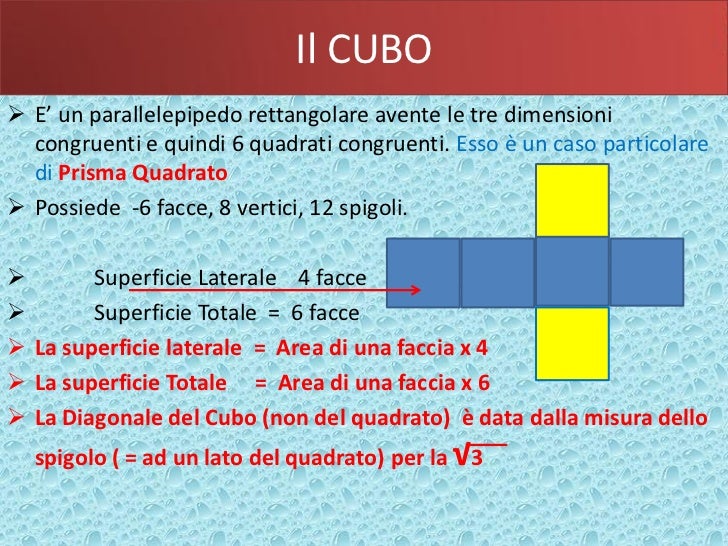
Lo spigolo di un cubo rappresenta semplicemente uno dei suoi lati. Più precisamente, è il segmento di retta che congiunge due vertici adiacenti, definendo uno dei bordi della figura tridimensionale. Immagina un dado: ogni linea che forma il bordo di una delle sue facce è uno spigolo.
Che Cosa Significa "Spigolo"?
La parola "spigolo" deriva dal latino "spiculum", che significa "punta" o "spina". In geometria, lo spigolo non si limita solo ai cubi, ma si riferisce al segmento di retta dove due facce di un solido si incontrano. Quindi, in termini più generali, lo spigolo è l'intersezione tra due superfici in un solido tridimensionale.
Perché lo Spigolo è Importante?
La comprensione del concetto di spigolo è fondamentale per diverse ragioni, soprattutto nell'apprendimento della geometria e della matematica. Esso rappresenta un elemento costitutivo essenziale per la comprensione delle proprietà e delle caratteristiche dei solidi geometrici.
Influenza sull'Apprendimento
Capire cos'è uno spigolo permette agli studenti di:
- Calcolare il perimetro delle facce di un cubo.
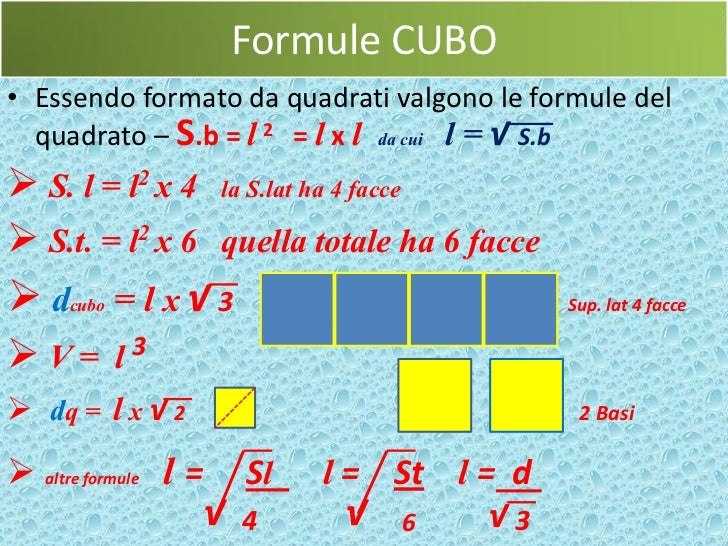
- Calcolare l'area superficiale totale del cubo (dato che l'area di ogni faccia è determinata dalla lunghezza dello spigolo).
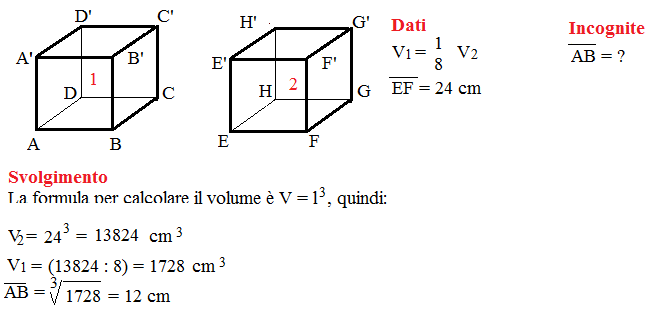
- Calcolare il volume del cubo (volume = spigolo x spigolo x spigolo).
- Visualizzare e comprendere meglio le figure tridimensionali.
- Risolvere problemi di geometria e matematica più complessi che coinvolgono solidi.
Senza una solida comprensione del concetto di spigolo, gli studenti potrebbero avere difficoltà a visualizzare le relazioni spaziali e a risolvere problemi che richiedono la manipolazione mentale di figure tridimensionali. Questo, a sua volta, potrebbe influire negativamente sul loro rendimento in matematica e scienze.
Ricerca e Opinioni di Esperti
Molti esperti di didattica della matematica sottolineano l'importanza di utilizzare materiali manipolativi, come cubi reali o modelli tridimensionali, per aiutare gli studenti a comprendere il concetto di spigolo. Maria Montessori, ad esempio, promuoveva l'uso di materiali concreti per facilitare l'apprendimento dei concetti astratti.
"La mano è lo strumento dell'intelligenza dell'uomo." - Maria Montessori
Secondo studi nel campo della psicologia dell'apprendimento, l'apprendimento attivo, che coinvolge la manipolazione fisica degli oggetti, favorisce una migliore comprensione e memorizzazione dei concetti. "L'apprendimento significativo si verifica quando le nuove informazioni si collegano a concetti preesistenti nella struttura cognitiva dello studente," afferma David Ausubel, noto psicologo dell'educazione.
Applicazioni Pratiche a Scuola e nella Vita Quotidiana
La comprensione del concetto di spigolo ha numerose applicazioni pratiche nella vita quotidiana degli studenti:
- A Scuola: Calcolare la quantità di materiale necessaria per costruire una scatola a forma di cubo, determinare il volume di un contenitore per un esperimento scientifico.
- A Casa: Aiutare a costruire un modellino di un edificio che utilizza forme cubiche, comprendere le dimensioni di un mobile a forma di cubo per decidere se entra in una stanza.
- Giochi: Capire le regole di giochi che coinvolgono dadi o costruzioni con cubi.
Inoltre, la comprensione degli spigoli può essere utile in discipline come l'arte e il design, dove la visualizzazione e la manipolazione di forme tridimensionali sono competenze essenziali.
In conclusione, lo spigolo di un cubo è un concetto fondamentale in geometria che, se ben compreso, apre le porte a una migliore comprensione delle figure tridimensionali e a un successo maggiore in matematica e scienze.