Punto Di Intersezione Delle Altezze Di Un Triangolo

Avete mai osservato un triangolo e vi siete chiesti se ci fosse un punto speciale dove le sue altezze si incontrano? Questo punto esiste, e si chiama ortocentro. Questo articolo è pensato per studenti di geometria, appassionati di matematica e chiunque sia curioso di approfondire le proprietà dei triangoli. Esploreremo l'ortocentro in dettaglio, fornendo definizioni chiare, proprietà e dimostrazioni, il tutto in modo accessibile e interessante.

Cos'è l'Ortocentro?

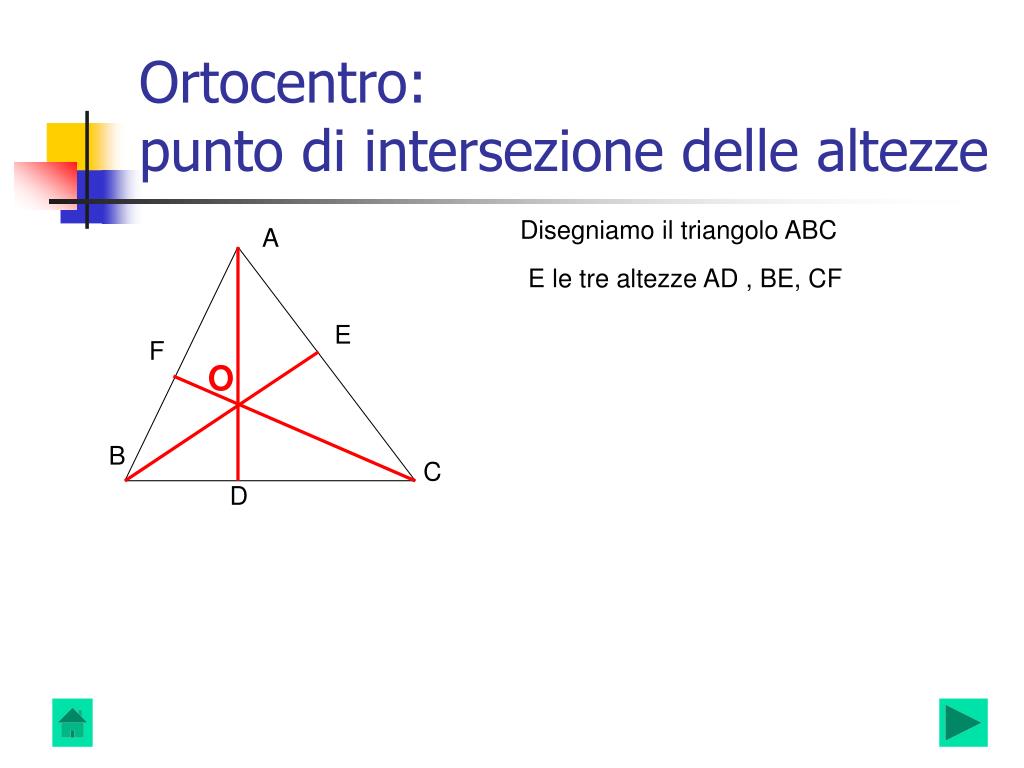
L'ortocentro di un triangolo è il punto di intersezione delle sue altezze. Ma cosa sono esattamente le altezze di un triangolo?

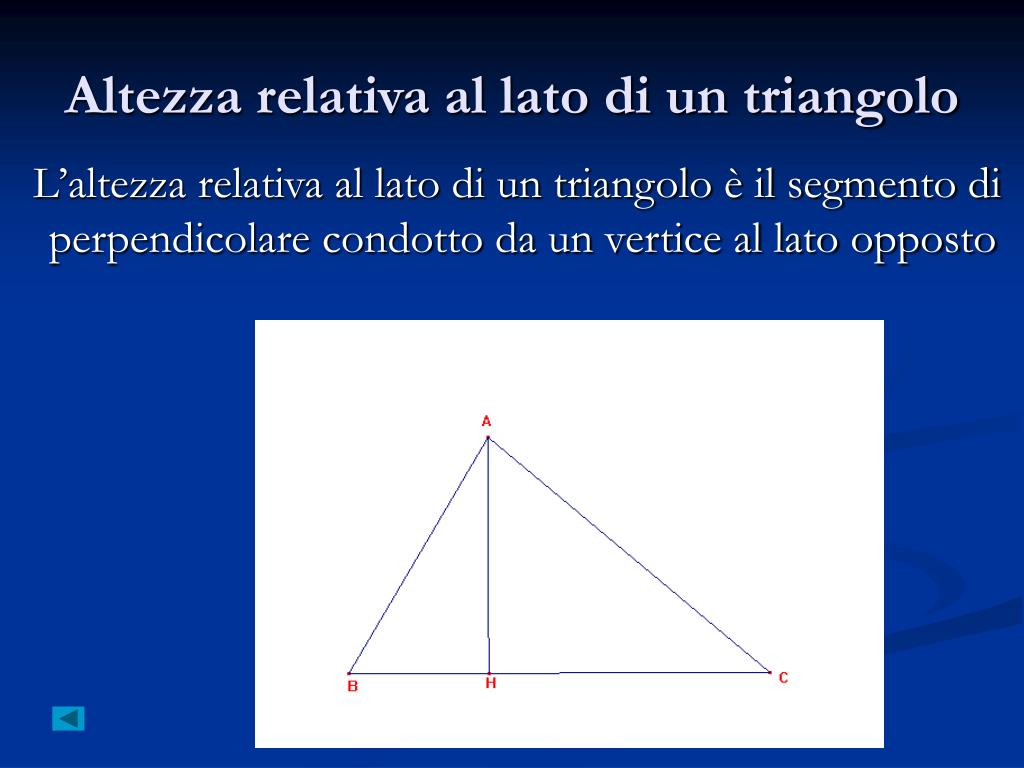
• Altezza: Un'altezza di un triangolo è un segmento di retta che parte da un vertice e cade perpendicolarmente sul lato opposto (o sul suo prolungamento). Ogni triangolo ha tre altezze, una per ciascun vertice.
• Ortocentro: Il punto in cui queste tre altezze si incontrano è l'ortocentro del triangolo.

È importante notare che l'ortocentro può trovarsi all'interno del triangolo, all'esterno del triangolo, oppure coincidere con uno dei suoi vertici, a seconda del tipo di triangolo.

Tipi di Triangoli e la Posizione dell'Ortocentro

La posizione dell'ortocentro varia a seconda del tipo di triangolo:

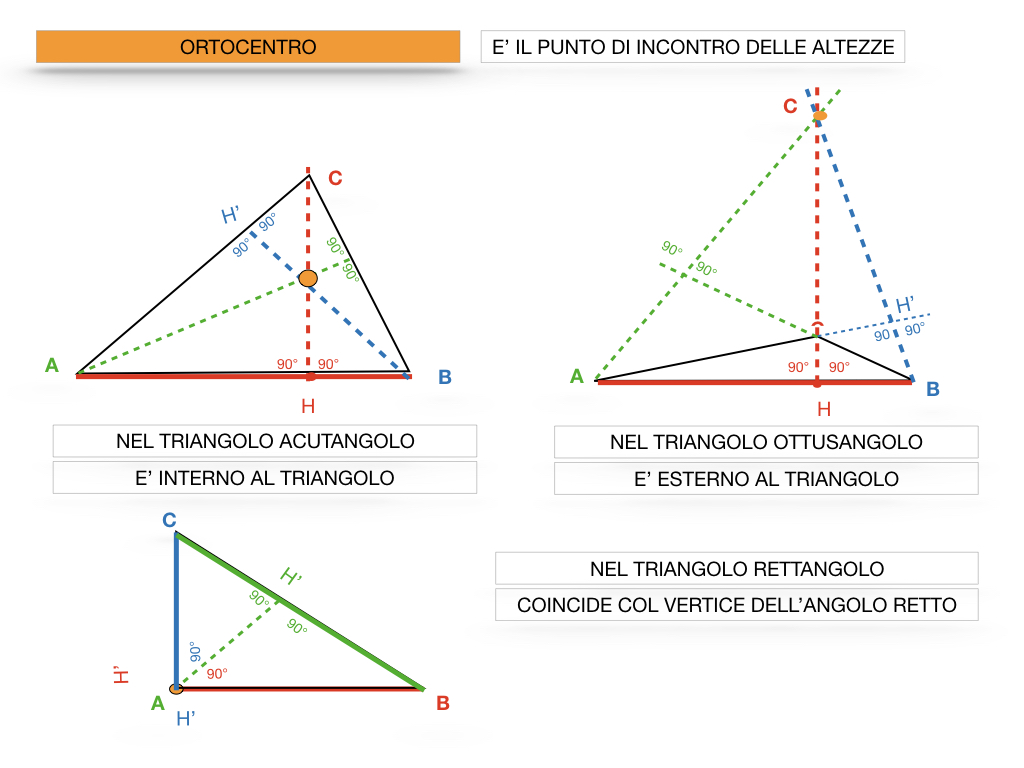
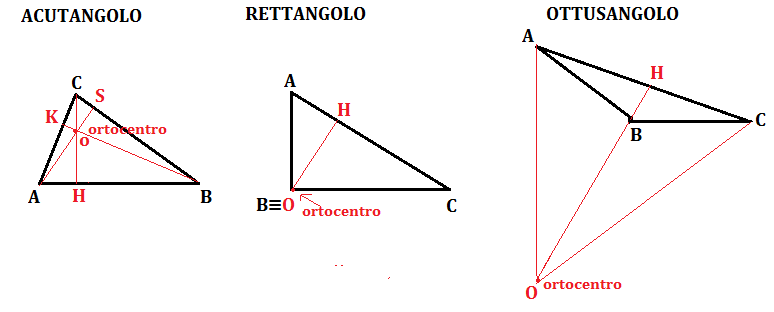
• Triangolo Acutangolo: In un triangolo acutangolo (tutti gli angoli interni sono minori di 90°), l'ortocentro si trova all'interno del triangolo.
• Triangolo Ottusangolo: In un triangolo ottusangolo (un angolo interno è maggiore di 90°), l'ortocentro si trova all'esterno del triangolo.
• Triangolo Rettangolo: In un triangolo rettangolo (un angolo interno è di 90°), l'ortocentro coincide con il vertice dell'angolo retto.

Come Trovare l'Ortocentro

Esistono diversi metodi per trovare l'ortocentro di un triangolo. Possiamo farlo graficamente o analiticamente.

Metodo Grafico

Il metodo grafico è il più intuitivo e si basa sulla costruzione delle altezze:

1. Disegna il triangolo.
2. Per ciascun vertice, traccia una retta perpendicolare al lato opposto (o al suo prolungamento). Puoi usare una squadra o un compasso per assicurarti che la retta sia perpendicolare.
3. Le tre rette si intersecheranno in un punto. Questo punto è l'ortocentro.

Metodo Analitico

Il metodo analitico utilizza le equazioni delle rette per calcolare le coordinate dell'ortocentro. Questo metodo è più preciso, ma richiede una conoscenza di base di geometria analitica.

Supponiamo di conoscere le coordinate dei vertici del triangolo: A(x₁, y₁), B(x₂, y₂) e C(x₃, y₃). I passaggi sono:

1. Calcola le pendenze dei lati: Trova le pendenze delle rette AB e BC (o di altri due lati). La pendenza di una retta passante per due punti (x₁, y₁) e (x₂, y₂) è data da (y₂ - y₁) / (x₂ - x₁).
2. Calcola le pendenze delle altezze: Le altezze sono perpendicolari ai lati. La pendenza di una retta perpendicolare a una retta con pendenza m è -1/m. Quindi, trova le pendenze delle altezze relative ai lati di cui hai calcolato le pendenze.
3. Trova le equazioni delle altezze: Utilizza la forma punto-pendenza dell'equazione di una retta: y - y₁ = m(x - x₁), dove (x₁, y₁) è un punto sulla retta e m è la sua pendenza. Usa le coordinate di un vertice e la pendenza dell'altezza corrispondente per trovare l'equazione di ciascuna altezza.
4. Risolvi il sistema di equazioni: Risolvi il sistema di equazioni formato dalle equazioni di due altezze. La soluzione (x, y) di questo sistema è l'ortocentro del triangolo.

Proprietà dell'Ortocentro

L'ortocentro ha diverse proprietà interessanti:

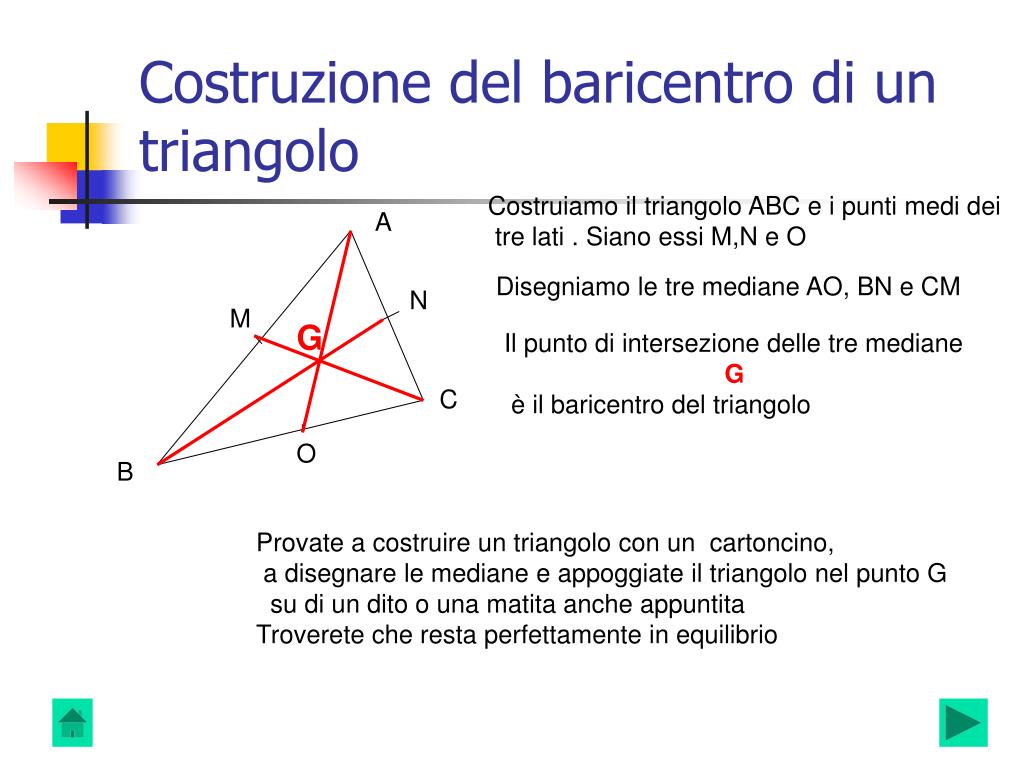
• Relazione con il Circocentro e il Baricentro: L'ortocentro, il circocentro (il centro della circonferenza circoscritta al triangolo) e il baricentro (il punto di incontro delle mediane) sono allineati sulla retta di Eulero. Questa è una proprietà notevole che collega tre punti speciali del triangolo.
• Ortocentro come Incentro: In un triangolo acutangolo, l'ortocentro è l'incentro (il centro della circonferenza inscritta) del triangolo ortico (il triangolo formato dai piedi delle altezze).
• Trasformazioni Geometriche: L'ortocentro si trasforma in modi specifici sotto le trasformazioni geometriche come traslazioni, rotazioni e riflessioni. Comprendere come l'ortocentro cambia con queste trasformazioni può fornire ulteriori intuizioni sulla sua natura.

Dimostrazioni Importanti

Dimostrare che le tre altezze di un triangolo si incontrano in un unico punto (l'ortocentro) richiede un po' di geometria. Ci sono diverse dimostrazioni possibili, una delle quali utilizza il concetto di triangolo simile.

Dimostrazione utilizzando Triangoli Simili

Consideriamo un triangolo ABC. Costruiamo le altezze AD, BE e CF. Vogliamo dimostrare che queste tre rette si incontrano in un punto.

1. Considera i triangoli AEH e BDH: Questi sono triangoli rettangoli. Inoltre, l'angolo ∠AHE = ∠BHD (angoli opposti al vertice). Pertanto, i triangoli AEH e BDH sono simili (per il criterio angolo-angolo).
2. Implicazioni della somiglianza: Dalla somiglianza dei triangoli, possiamo dedurre che AH/BH = EH/DH.
3. Considera i triangoli AFH e CDH: Analogamente, questi sono triangoli rettangoli e l'angolo ∠AHF = ∠CHD. Quindi, i triangoli AFH e CDH sono simili, e AH/CH = FH/DH.
4. Relazione tra le altezze: Manipolando queste proporzioni e utilizzando altre relazioni geometriche all'interno del triangolo, si può dimostrare che le tre altezze concorrono in un punto. La dimostrazione completa è un po' complessa e richiede ulteriori passaggi, ma l'idea chiave è quella di sfruttare la somiglianza dei triangoli formati dalle altezze.

Una dimostrazione alternativa può essere realizzata utilizzando coordinate cartesiane e algebra lineare, definendo le equazioni delle rette contenenti le altezze e dimostrando che il sistema formato dalle equazioni di due di esse ammette una soluzione che soddisfa anche l'equazione della terza altezza.

Esempi Pratici e Applicazioni

L'ortocentro non è solo un concetto teorico; ha applicazioni pratiche in vari campi, tra cui:

• Architettura e Ingegneria: Nella progettazione di strutture, la comprensione delle proprietà dei triangoli, inclusa la posizione dell'ortocentro, può essere utile per garantire la stabilità e la distribuzione del peso.
• Navigazione e Cartografia: I triangoli sono fondamentali in cartografia e navigazione. Conoscere le proprietà come l'ortocentro può aiutare a risolvere problemi legati alla triangolazione e al posizionamento.
• Grafica Computerizzata e Animazione: I triangoli sono i blocchi di costruzione fondamentali nella grafica computerizzata. La manipolazione e la comprensione delle loro proprietà, inclusa la posizione di punti speciali come l'ortocentro, è essenziale per creare modelli 3D e animazioni.

Perché l'Ortocentro è Importante?

L'ortocentro è importante per diversi motivi:

• Completa la nostra comprensione dei triangoli: Studiare l'ortocentro ci aiuta a capire meglio le relazioni tra i diversi elementi di un triangolo, come i vertici, i lati e gli angoli.
• Fornisce uno strumento per risolvere problemi geometrici: La conoscenza dell'ortocentro può essere utile per risolvere problemi di geometria più complessi.
• Collega diversi concetti matematici: L'ortocentro è legato ad altri punti speciali del triangolo (circocentro, baricentro) e alla retta di Eulero, dimostrando la profonda interconnessione dei concetti matematici.

Conclusione

L'ortocentro è un punto affascinante all'interno di un triangolo che rivela molto sulla geometria e le proprietà di questa figura fondamentale. Speriamo che questo articolo vi abbia fornito una comprensione chiara e approfondita dell'ortocentro, dalla sua definizione ai suoi metodi di calcolo, alle sue proprietà e alle sue applicazioni. Continuate a esplorare il mondo della geometria, perché ogni figura e ogni punto speciale ha una storia da raccontare. La prossima volta che vedete un triangolo, ricordatevi dell'ortocentro e della sua posizione unica: un punto di incontro, un punto di equilibrio, un punto di scoperta!