Proiezioni Ortogonali Piramide A Base Quadrata

Ciao a tutti! Capisco perfettamente come ci si sente quando si affrontano le proiezioni ortogonali, specialmente quando si tratta di una piramide a base quadrata. Sembra complicato, vero? Ma non preoccupatevi! Insieme, passo dopo passo, renderemo questo argomento chiaro e accessibile. Molti studenti mi dicono che inizialmente si sentono sopraffatti, ma una volta compresi i concetti base, tutto diventa più semplice. Come dice la professoressa Rossi, insegnante di geometria da oltre 20 anni: "La chiave è visualizzare l'oggetto nello spazio e poi riportarlo sul piano. Con un po' di pratica, tutti possono farcela!".

L'obiettivo di questo articolo è proprio questo: guidarvi in modo chiaro e pratico attraverso il mondo delle proiezioni ortogonali, concentrandoci sulla piramide a base quadrata. Dimenticate il gergo tecnico e preparatevi a un'esperienza di apprendimento divertente e stimolante.

Cos'è una Proiezione Ortogonale?

Innanzitutto, cerchiamo di capire cosa sono le proiezioni ortogonali. Immaginate di avere un oggetto tridimensionale (come la nostra piramide) e di illuminarlo con una forte luce. L'ombra che questo oggetto proietta su una parete è una proiezione. La proiezione ortogonale è un tipo speciale di proiezione dove i raggi di luce sono perpendicolari (formano un angolo di 90 gradi) alla parete (il piano di proiezione).

In pratica, le proiezioni ortogonali ci permettono di rappresentare un oggetto tridimensionale su un foglio di carta bidimensionale. Usiamo tre piani di proiezione principali: il Piano Orizzontale (PO), il Piano Verticale (PV) e il Piano Laterale (PL). Pensate a questi piani come le pareti di una stanza, dove ogni parete mostra una "vista" diversa dell'oggetto.

La Piramide a Base Quadrata: un Soggetto Perfetto

Perché usiamo proprio la piramide a base quadrata? Perché è una forma geometrica relativamente semplice, ma che presenta diverse sfide interessanti dal punto di vista delle proiezioni. Ha una base quadrata, che è facile da visualizzare, e un vertice che si proietta in modo differente a seconda della sua posizione.

Come Rappresentare la Piramide: Passo dopo Passo

Ora vediamo come rappresentare la piramide a base quadrata sui nostri tre piani di proiezione. Prendiamo in considerazione una piramide con la base appoggiata sul PO. Questo semplifica un po' le cose all'inizio.

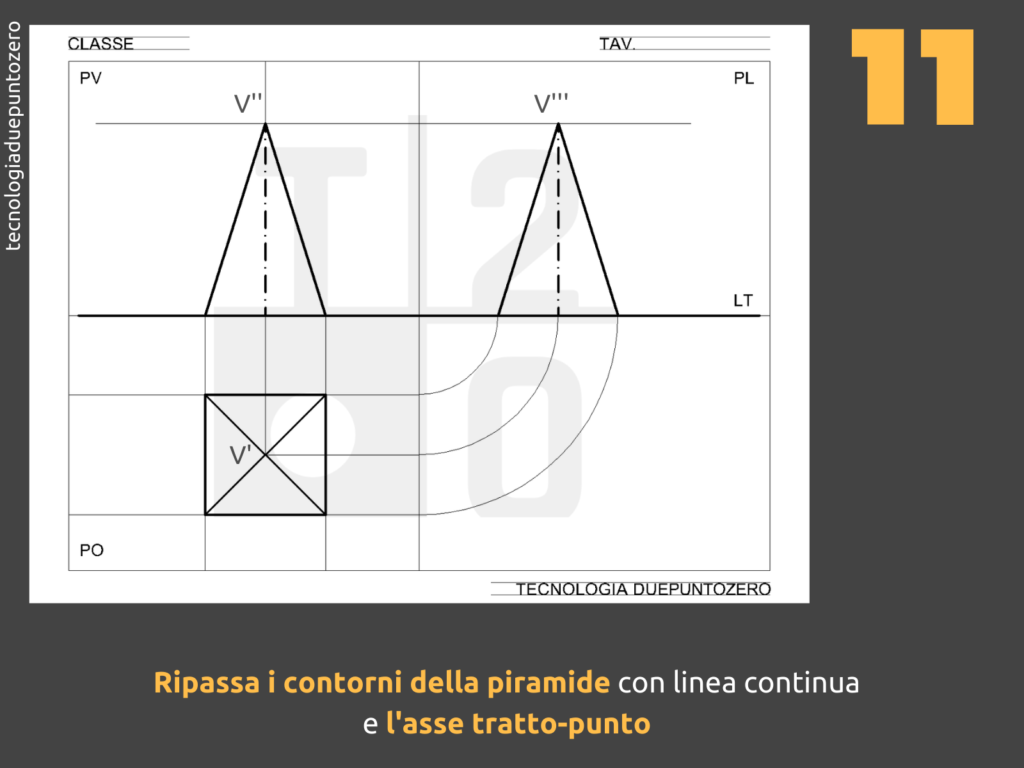
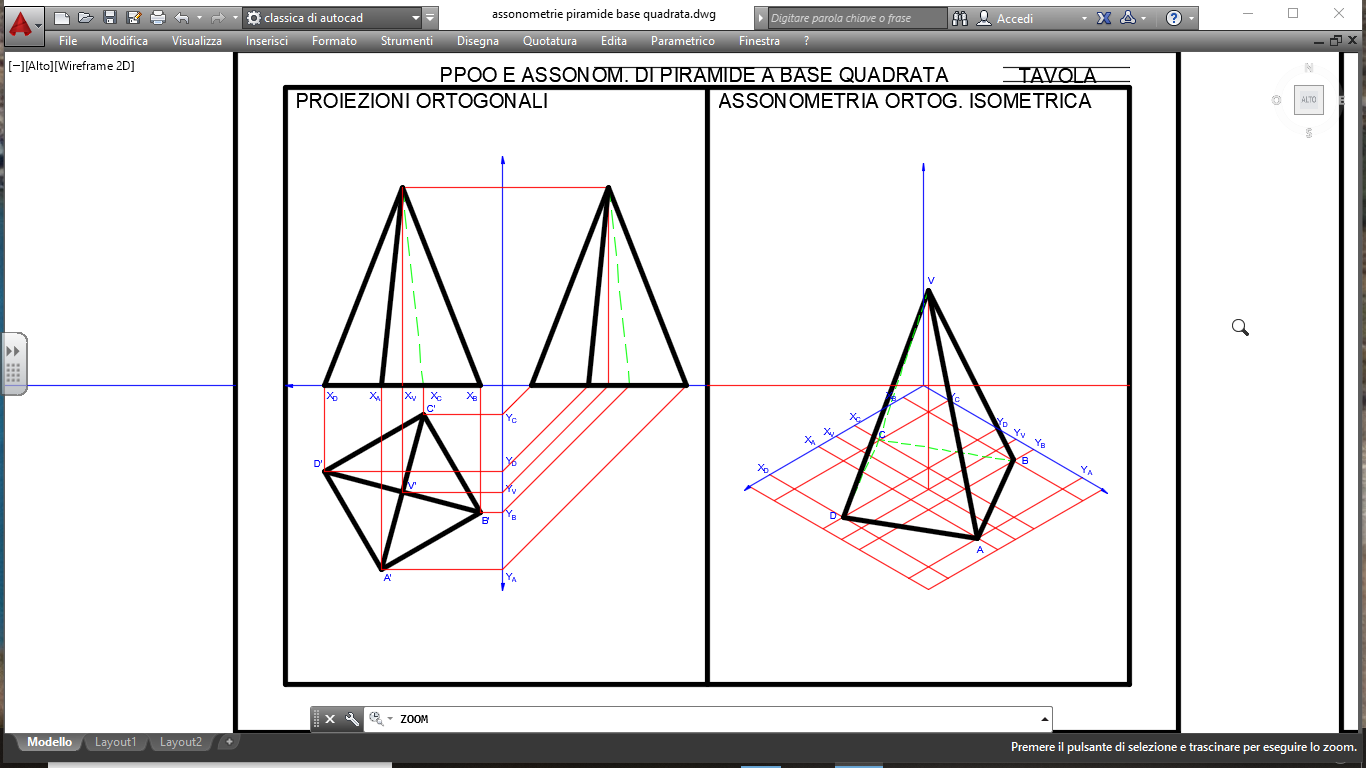
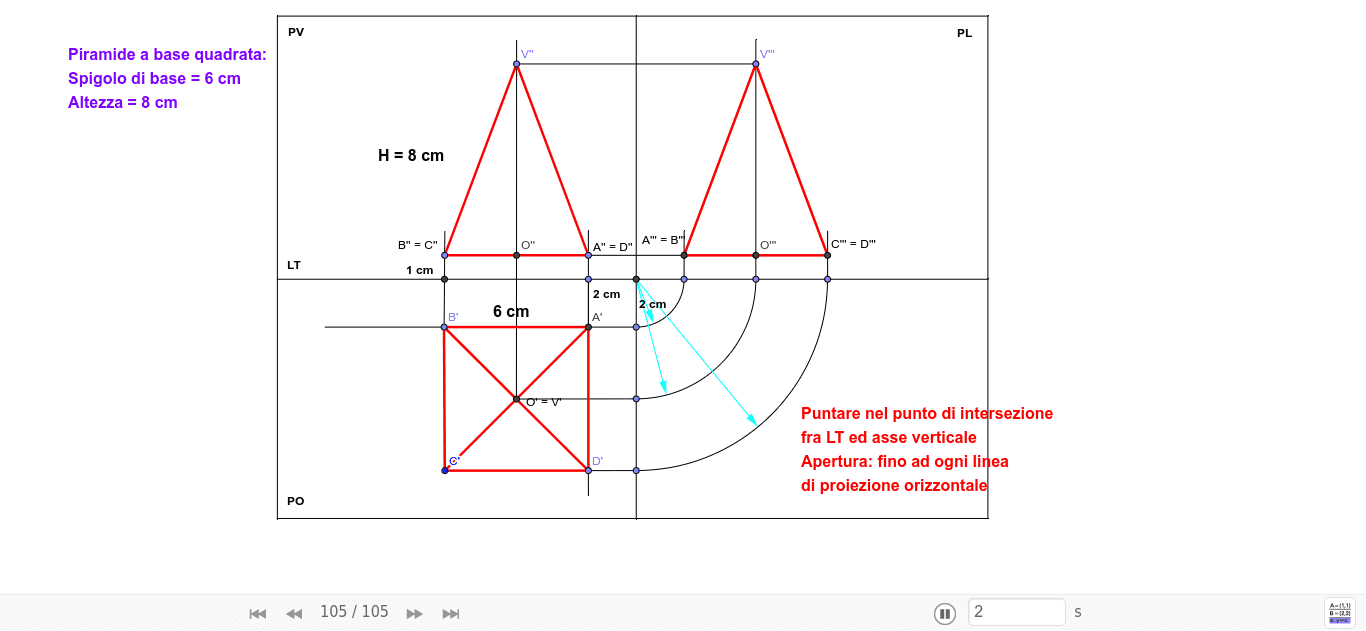
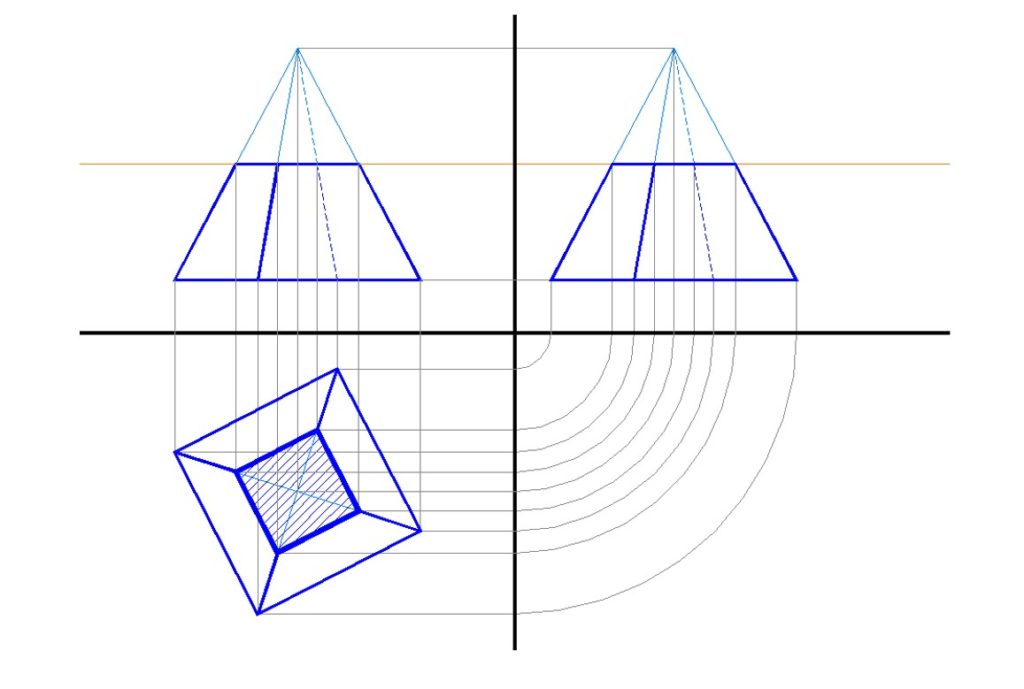
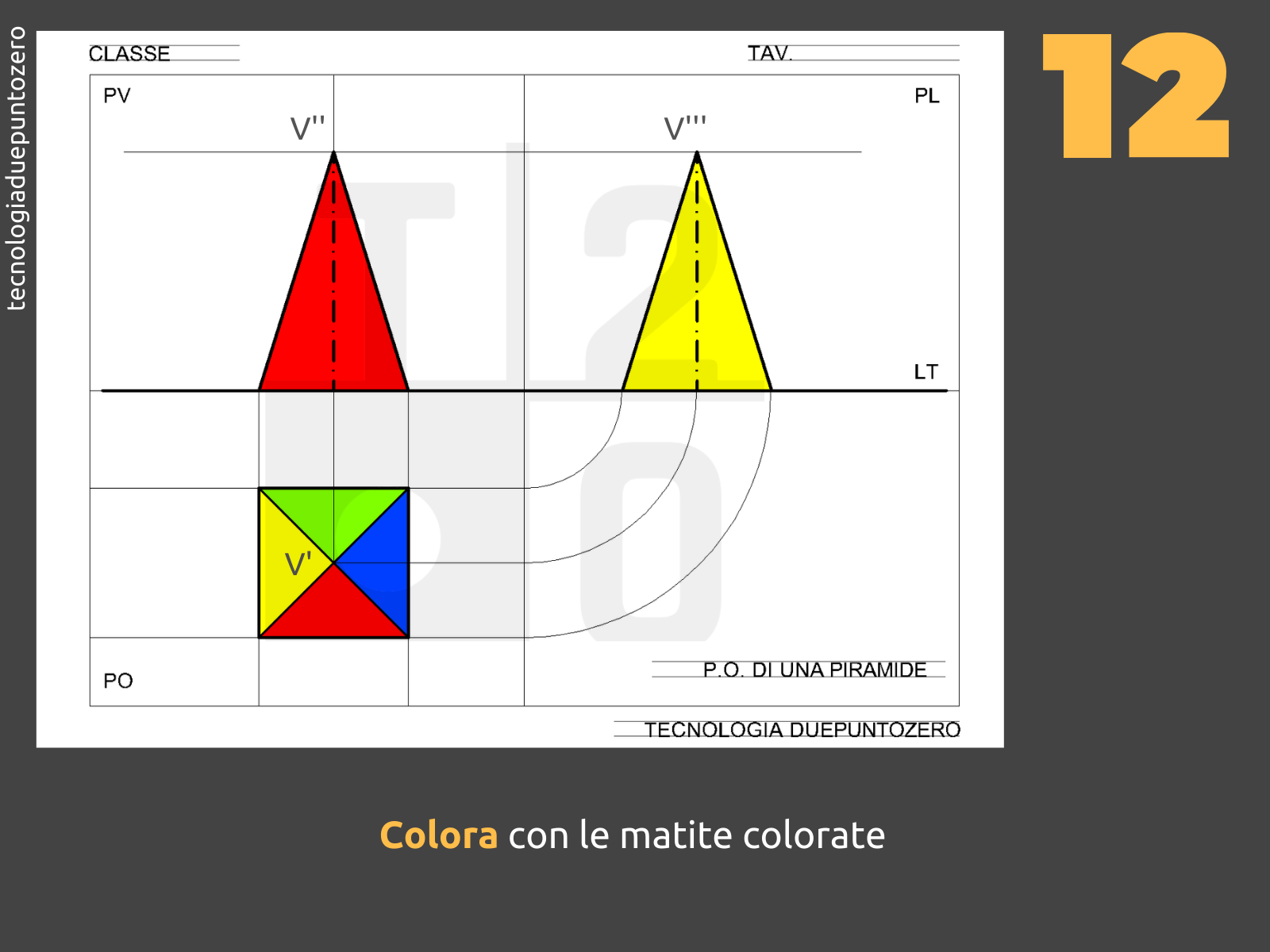
1. Sul Piano Orizzontale (PO): La proiezione sul PO è semplicemente un quadrato. Se la piramide è appoggiata con la base sul PO, vedremo esattamente la sua base. Ricordate di indicare il centro del quadrato, che rappresenta la proiezione del vertice della piramide.
2. Sul Piano Verticale (PV): La proiezione sul PV è un triangolo isoscele. L'altezza del triangolo rappresenta l'altezza della piramide, e la base del triangolo rappresenta il lato del quadrato di base. Il vertice del triangolo corrisponde al vertice della piramide.
3. Sul Piano Laterale (PL): La proiezione sul PL è identica a quella sul PV: un altro triangolo isoscele. Questo perché la piramide ha una base quadrata, quindi le due viste laterali sono simmetriche.

Esercizio pratico: Disegnate su un foglio i tre piani (PO, PV, PL) come se fossero le pareti di una stanza. Ora, disegnate le proiezioni della piramide su ciascun piano, seguendo le indicazioni sopra. Non abbiate paura di sbagliare! L'importante è provare e sperimentare.

Complicazioni e Variazioni

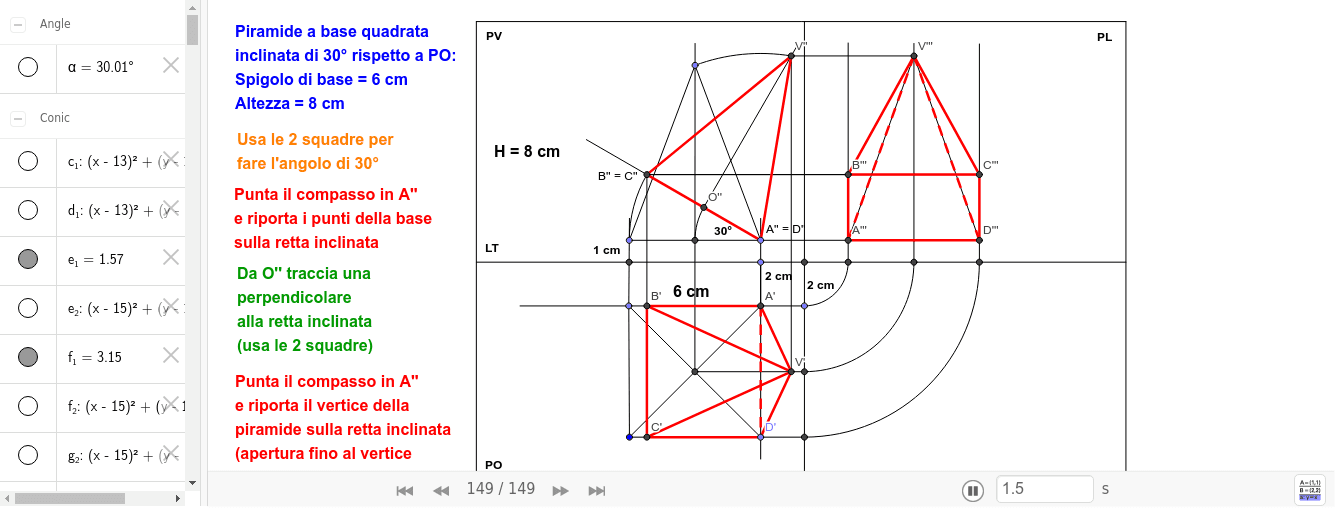
Cosa succede se la piramide non è appoggiata con la base sul PO? Qui le cose si fanno un po' più interessanti. Se la piramide è sollevata dal PO, o inclinata, le proiezioni cambieranno. Ad esempio:

• Se la piramide è sollevata dal PO, la proiezione sul PO sarà sempre un quadrato, ma non toccherà la linea di terra (la linea che separa il PO dal PV e dal PL).
• Se la piramide è inclinata, la proiezione sul PV e sul PL non sarà più un triangolo isoscele, ma un triangolo scaleno.

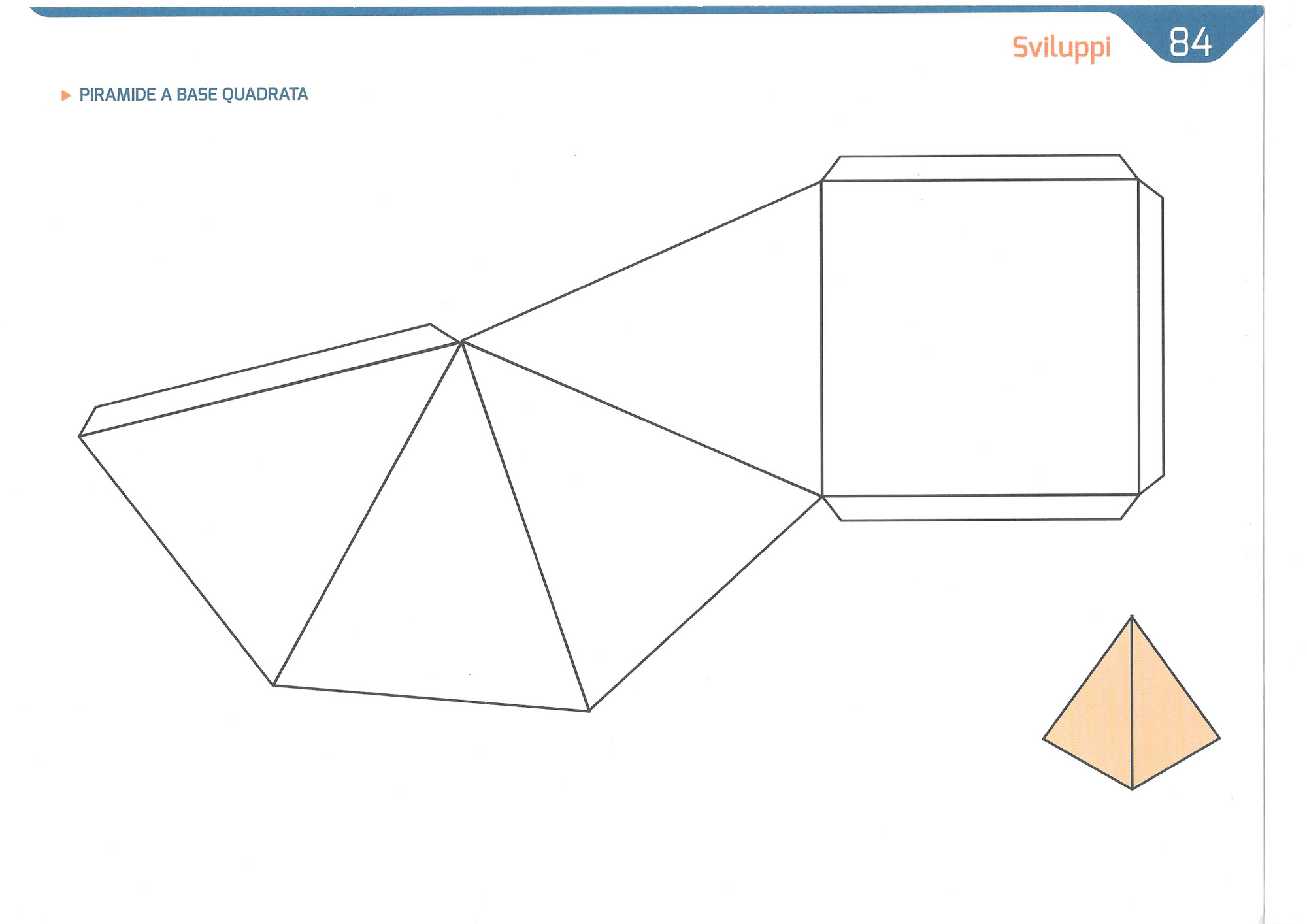
Consiglio: Per visualizzare meglio queste variazioni, provate a costruire un piccolo modello di piramide con la carta. Potete poi manipolarlo e osservare come cambiano le proiezioni su una superficie illuminata.

Trucchi e Consigli per il Successo

Ecco alcuni trucchi e consigli che vi aiuteranno a padroneggiare le proiezioni ortogonali della piramide a base quadrata:

• Visualizzazione Spaziale: Cercate di sviluppare la vostra capacità di visualizzazione spaziale. Immaginate la piramide nella vostra mente e ruotatela. Questo vi aiuterà a capire come le proiezioni cambiano a seconda dell'orientamento.
• Pratica, Pratica, Pratica: Come per ogni abilità, la pratica è fondamentale. Fate tanti esercizi diversi, variando la posizione e l'orientamento della piramide.
• Utilizzate Risorse Online: Ci sono molti tutorial e risorse online che possono aiutarvi a capire meglio le proiezioni ortogonali. Cercate video su YouTube o siti web dedicati al disegno tecnico.
• Non Abbiate Paura di Chiedere Aiuto: Se avete difficoltà, non esitate a chiedere aiuto al vostro insegnante, ai vostri compagni di classe o a un tutor.

Molti studenti trovano utile utilizzare software di modellazione 3D per visualizzare le proiezioni ortogonali. Anche se non è necessario, può essere un ottimo strumento per comprendere meglio i concetti.

Esercizi Pratici Avanzati

Ecco alcuni esercizi più avanzati per mettere alla prova le vostre abilità:

1. Disegnate le proiezioni ortogonali di una piramide a base quadrata con un lato della base parallelo al PV e l'altro parallelo al PL.
2. Disegnate le proiezioni ortogonali di una piramide a base quadrata con l'asse inclinato rispetto al PO.
3. Disegnate le proiezioni ortogonali di una piramide a base quadrata intersecata da un piano.

Questi esercizi vi aiuteranno a sviluppare una comprensione più profonda delle proiezioni ortogonali e a prepararvi per sfide ancora più complesse.

Applicazioni Quotidiane delle Proiezioni Ortogonali

Potreste chiedervi: "Ma a cosa serve tutto questo nella vita reale?". Le proiezioni ortogonali sono utilizzate in molti campi diversi, tra cui:

• Architettura: Gli architetti utilizzano le proiezioni ortogonali per creare planimetrie, prospetti e sezioni degli edifici.
• Ingegneria: Gli ingegneri utilizzano le proiezioni ortogonali per progettare e costruire macchinari, ponti e altre strutture.
• Design Industriale: I designer industriali utilizzano le proiezioni ortogonali per creare modelli 3D di prodotti.
• Animazione e Videogiochi: Anche se oggi si usano modelli 3D, la comprensione delle proiezioni ortogonali aiuta a creare texture e ambientazioni realistiche.

Capire le proiezioni ortogonali, quindi, apre le porte a molte opportunità di carriera interessanti.

Un Ultimo Incoraggiamento

Spero che questo articolo vi abbia aiutato a capire meglio le proiezioni ortogonali della piramide a base quadrata. Ricordate, la chiave è la pratica e la perseveranza. Non scoraggiatevi se all'inizio vi sembra difficile. Con un po' di impegno, sarete in grado di padroneggiare questo argomento e di applicarlo in molti contesti diversi.

Come diceva Albert Einstein: "Non preoccuparti delle tue difficoltà in matematica. Ti assicuro che le mie sono ancora maggiori". Quindi, prendete un respiro profondo, impugnate la matita e iniziate a disegnare! In bocca al lupo!