Proiezione Ortogonale Di Una Piramide A Base Quadrata
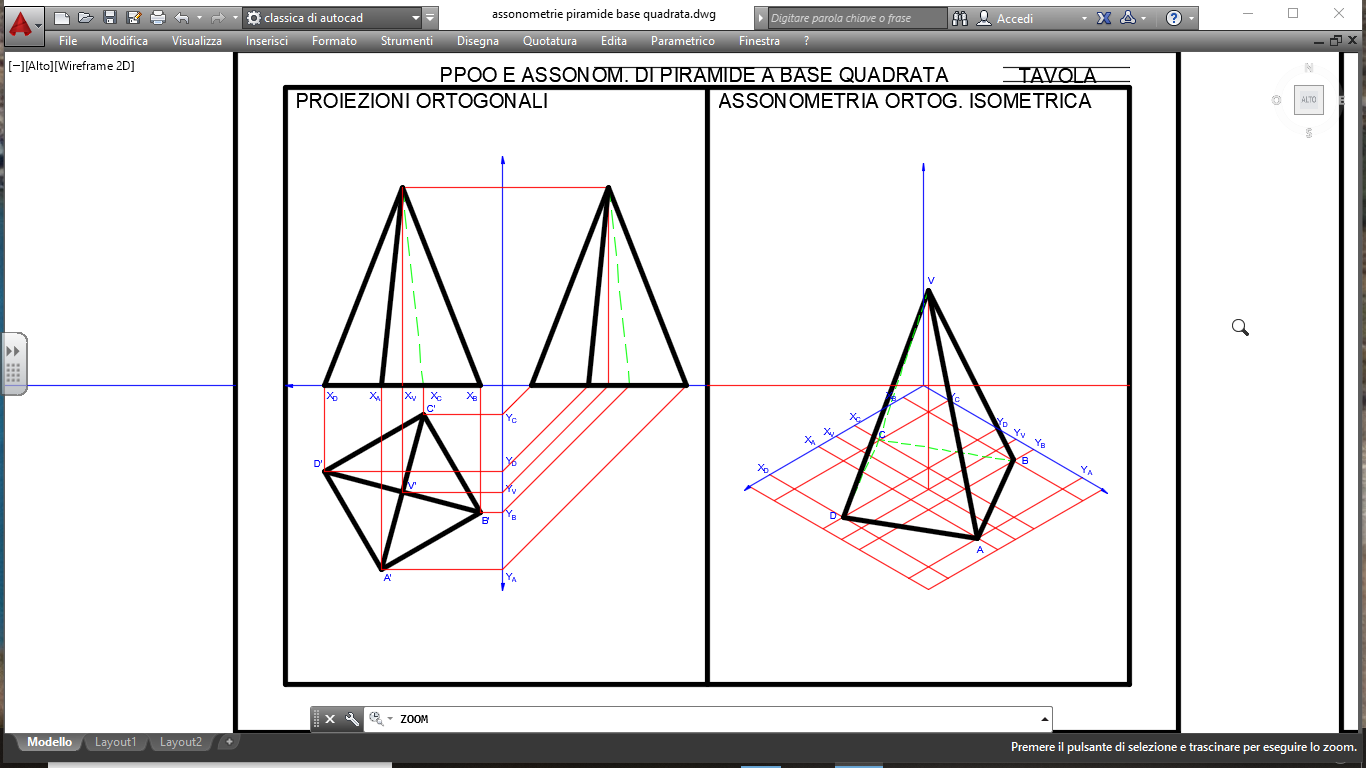
La proiezione ortogonale è un metodo fondamentale nella geometria descrittiva e nel disegno tecnico, utilizzato per rappresentare oggetti tridimensionali su un piano bidimensionale. Questo processo è essenziale per comunicare con precisione le caratteristiche geometriche di un oggetto, consentendo a ingegneri, architetti e designer di visualizzare e progettare strutture complesse. In questo articolo, esploreremo in dettaglio la proiezione ortogonale di una piramide a base quadrata, analizzando i passaggi chiave e i principi che governano questa tecnica.
Fondamenti della Proiezione Ortogonale
Prima di immergerci nella piramide, è cruciale comprendere i concetti base della proiezione ortogonale. In sintesi, si tratta di proiettare un oggetto su diversi piani di proiezione (tipicamente tre: orizzontale, verticale e laterale) utilizzando rette proiettanti perpendicolari a questi piani. Ogni punto dell'oggetto viene proiettato ortogonalmente sul piano, creando una rappresentazione bidimensionale dell'oggetto stesso.
Le proiezioni ottenute su ciascun piano forniscono informazioni diverse sull'oggetto. La proiezione orizzontale (vista dall'alto) mostra la forma e le dimensioni dell'oggetto in pianta. La proiezione verticale (vista frontale) mostra l'altezza e le forme verticali. La proiezione laterale (vista di lato) fornisce informazioni sulla profondità e sulle forme laterali. Queste tre proiezioni, combinate, offrono una rappresentazione completa dell'oggetto tridimensionale.
I Piani di Proiezione
I piani di proiezione sono fondamentali per la realizzazione della proiezione ortogonale. Solitamente, si utilizzano tre piani: il piano orizzontale (PO), il piano verticale (PV) e il piano laterale (PL). Questi piani sono mutuamente perpendicolari e formano un triedro trirettangolo.
- Piano Orizzontale (PO): Rappresenta la vista dall'alto dell'oggetto.
- Piano Verticale (PV): Rappresenta la vista frontale dell'oggetto.
- Piano Laterale (PL): Rappresenta la vista laterale dell'oggetto.
La linea di terra (LT) è l'intersezione tra il piano orizzontale e il piano verticale. Questa linea è fondamentale per allineare correttamente le proiezioni e garantire la coerenza tra le diverse viste.
Proiezione Ortogonale di una Piramide a Base Quadrata
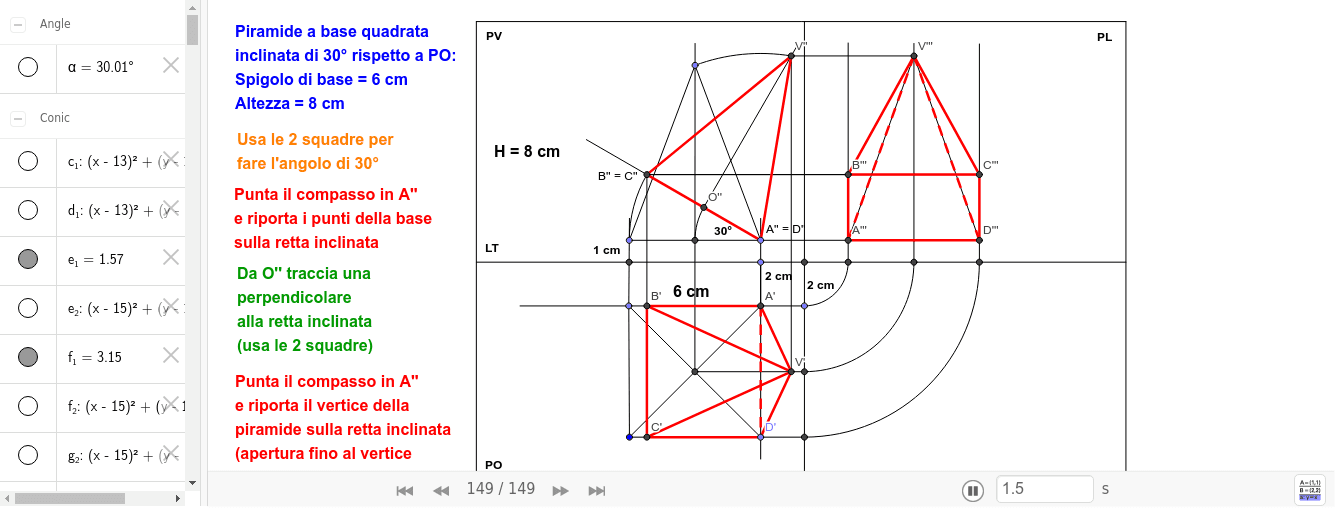
Ora, applichiamo questi principi alla proiezione ortogonale di una piramide a base quadrata. Una piramide a base quadrata è un solido geometrico composto da una base quadrata e quattro facce triangolari che convergono in un unico punto, chiamato vertice o apice della piramide.
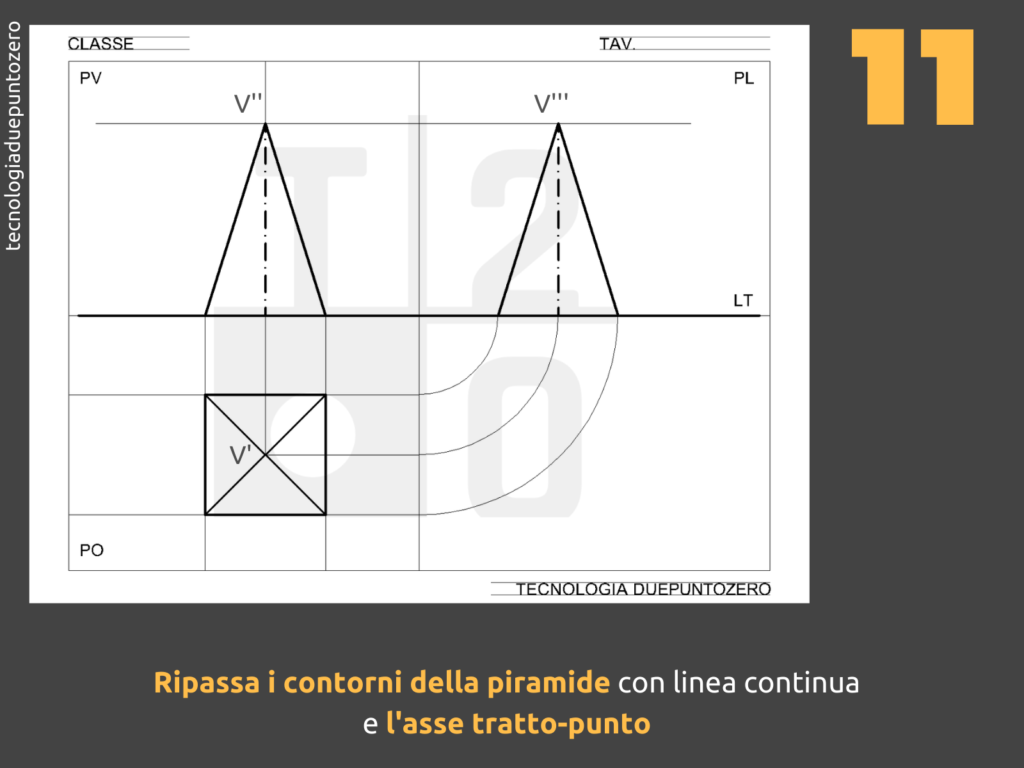
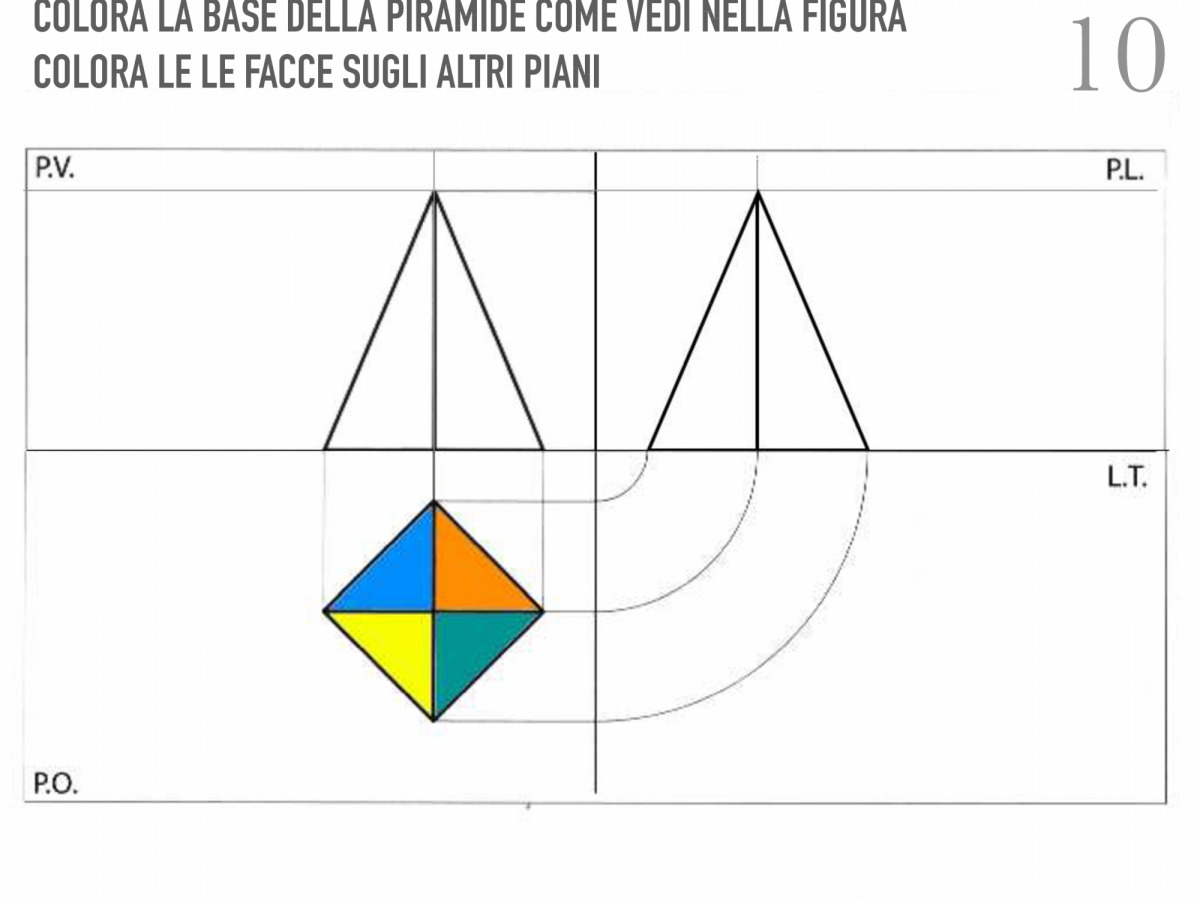
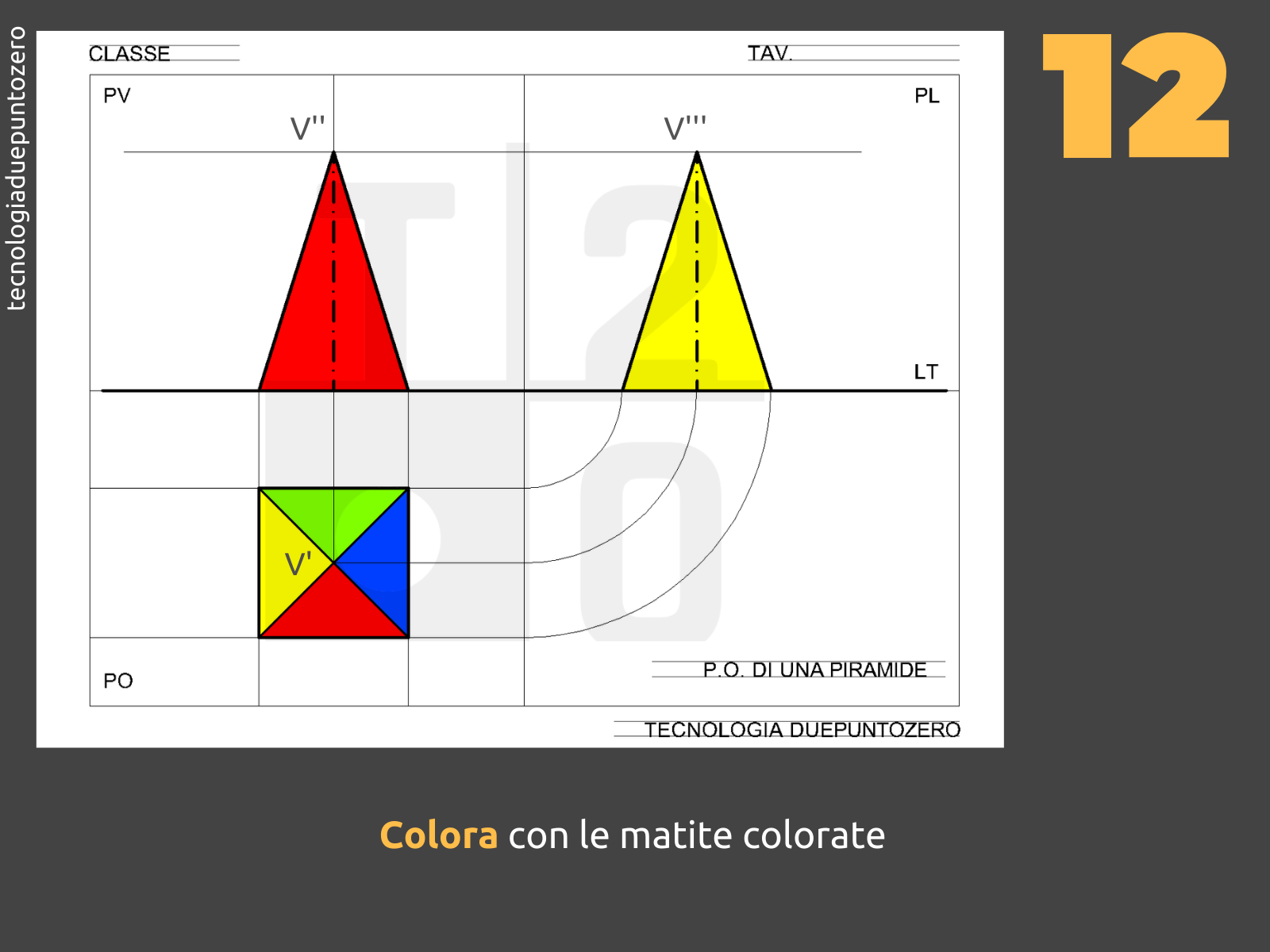
Proiezione sul Piano Orizzontale (PO)
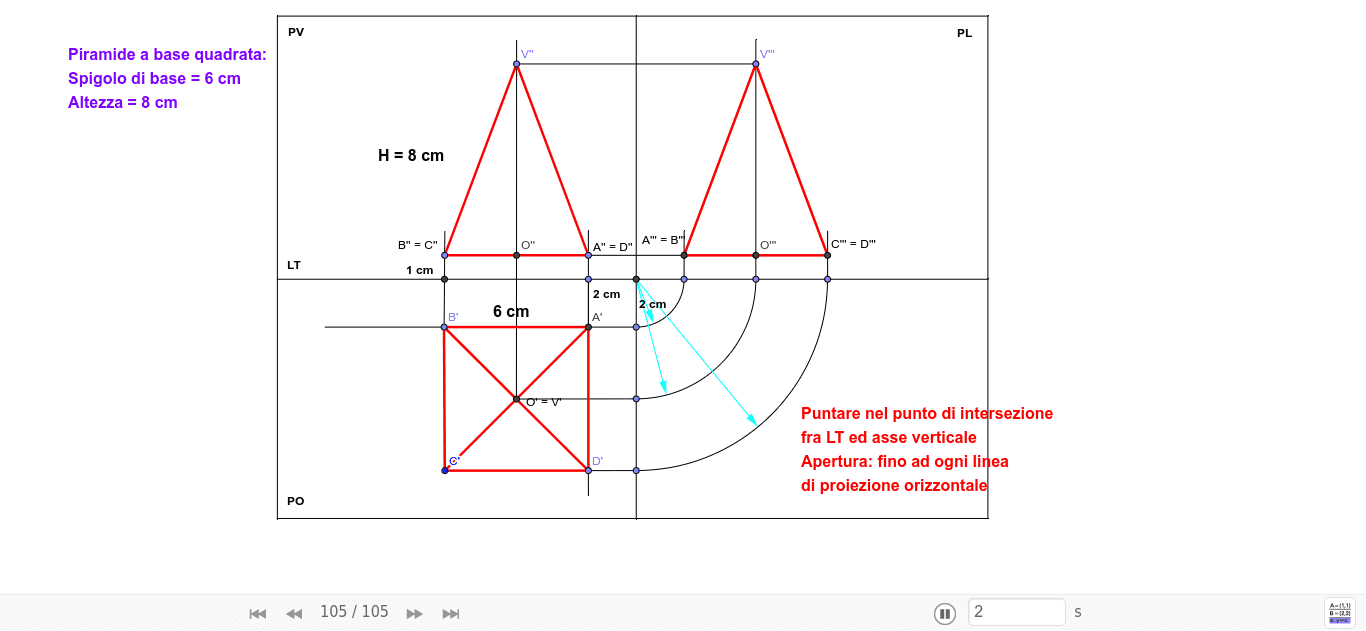
La proiezione sul piano orizzontale (PO) è la più semplice. La base quadrata della piramide viene proiettata come un quadrato. Se la piramide è posizionata con la base parallela al PO, il quadrato proiettato avrà le stesse dimensioni della base reale. Il vertice della piramide viene proiettato al centro del quadrato. Questo punto rappresenta la posizione del vertice vista dall'alto.
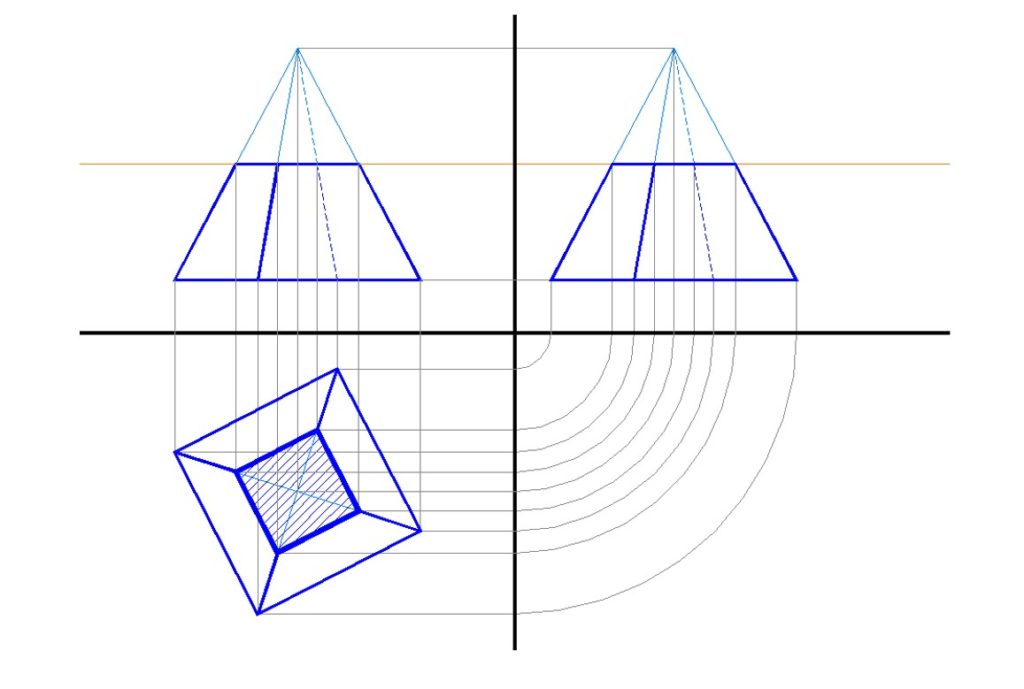
Se la piramide è inclinata rispetto al PO, la proiezione della base sarà un quadrilatero deformato (un parallelogramma o un trapezio, a seconda dell'inclinazione). La posizione del vertice proiettato all'interno del quadrilatero dipenderà dall'angolo di inclinazione.
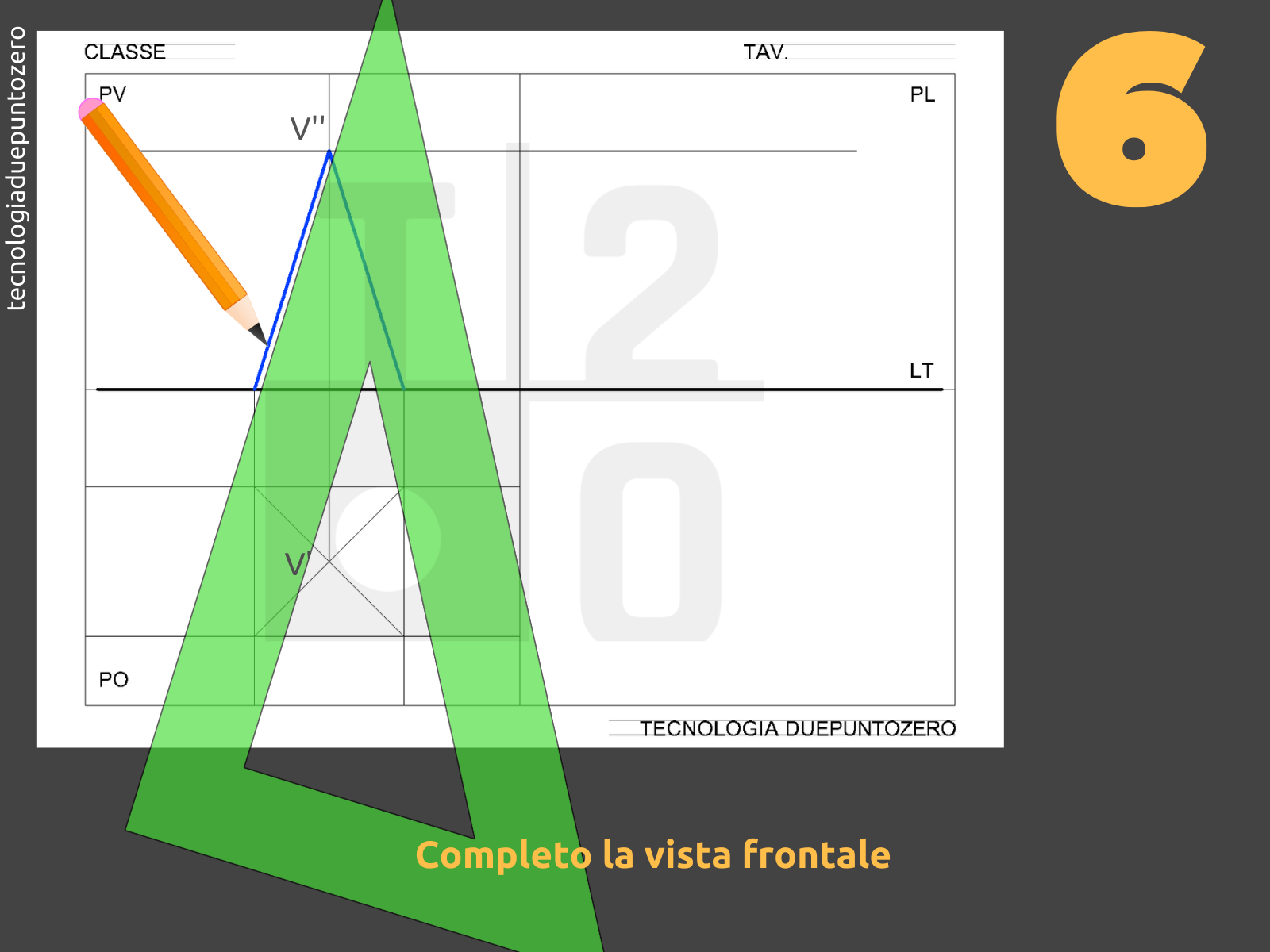
Proiezione sul Piano Verticale (PV)
La proiezione sul piano verticale (PV) mostra l'altezza della piramide. La base quadrata viene proiettata come un segmento (se una delle diagonali della base è parallela al PV) o come un trapezio (se la base è inclinata rispetto al PV). Il vertice della piramide viene proiettato come un punto sopra il segmento o il trapezio, all'altezza corretta rispetto alla base. Le facce triangolari della piramide si proiettano come triangoli che collegano la proiezione della base alla proiezione del vertice.
È importante notare che l'altezza della piramide nella proiezione verticale corrisponde alla distanza tra la proiezione della base e la proiezione del vertice. La forma dei triangoli proiettati dipende dall'orientamento della piramide rispetto al PV.
Proiezione sul Piano Laterale (PL)
La proiezione sul piano laterale (PL) è simile alla proiezione sul PV. Anche in questo caso, la base quadrata si proietta come un segmento o un trapezio, e il vertice si proietta come un punto. Le facce triangolari si proiettano come triangoli. La forma dei triangoli proiettati sul PL, però, sarà diversa rispetto a quella dei triangoli proiettati sul PV, a meno che la piramide non abbia una simmetria specifica rispetto a entrambi i piani.
La proiezione sul PL fornisce una vista "di lato" della piramide, complementare alla vista frontale offerta dal PV.
Esempio Pratico
Immaginiamo una piramide a base quadrata con lato di base di 5 cm e altezza di 8 cm. Posizioniamo la piramide con la base parallela al PO e una delle diagonali della base parallela al PV.
- PO: La proiezione sarà un quadrato di lato 5 cm, con un punto al centro che rappresenta il vertice.
- PV: La proiezione sarà un segmento di lunghezza pari alla diagonale del quadrato (circa 7.07 cm). Sopra questo segmento, a una distanza di 8 cm, ci sarà il punto che rappresenta il vertice. Le due facce triangolari visibili si proietteranno come triangoli con base sul segmento e vertice nel punto.
- PL: La proiezione sarà un segmento di lunghezza pari al lato del quadrato (5 cm). Sopra questo segmento, a una distanza di 8 cm, ci sarà il punto che rappresenta il vertice. Le due facce triangolari visibili si proietteranno come triangoli con base sul segmento e vertice nel punto. L'altezza dei triangoli sul PL sarà diversa rispetto all'altezza dei triangoli sul PV.
Questo semplice esempio illustra come le proiezioni sui diversi piani forniscono informazioni diverse sulla forma e le dimensioni della piramide.
Applicazioni Reali
La proiezione ortogonale è ampiamente utilizzata in diversi settori:
- Architettura: Per creare planimetrie, prospetti e sezioni di edifici.
- Ingegneria: Per progettare macchinari, componenti e strutture.
- Design Industriale: Per visualizzare e comunicare le caratteristiche di prodotti.
- Cartografia: Per rappresentare il territorio su mappe.
Ad esempio, un architetto utilizzerebbe la proiezione ortogonale per creare i disegni di un edificio, mostrando le viste in pianta, i prospetti e le sezioni. Un ingegnere meccanico utilizzerebbe la proiezione ortogonale per progettare un motore, creando viste dettagliate di ogni componente. Un designer industriale utilizzerebbe la proiezione ortogonale per presentare un nuovo prodotto, mostrando le sue dimensioni e il suo aspetto da diverse angolazioni.
Conclusioni
La proiezione ortogonale è uno strumento potente e versatile per rappresentare oggetti tridimensionali su un piano bidimensionale. La comprensione dei principi fondamentali della proiezione ortogonale e la capacità di applicarli a forme geometriche semplici come la piramide a base quadrata sono essenziali per chiunque lavori in settori che richiedono la visualizzazione e la comunicazione di informazioni geometriche. Esercitarsi con diversi esempi e sperimentare con diverse angolazioni e posizioni dell'oggetto è fondamentale per acquisire padronanza di questa tecnica.
Per approfondire la tua conoscenza, ti incoraggio a esplorare ulteriormente la geometria descrittiva e il disegno tecnico. Ci sono numerose risorse online, libri di testo e corsi che possono aiutarti a sviluppare le tue competenze in questo campo. Non smettere mai di imparare! La capacità di visualizzare e comunicare concetti geometrici è una competenza preziosa in molti settori.