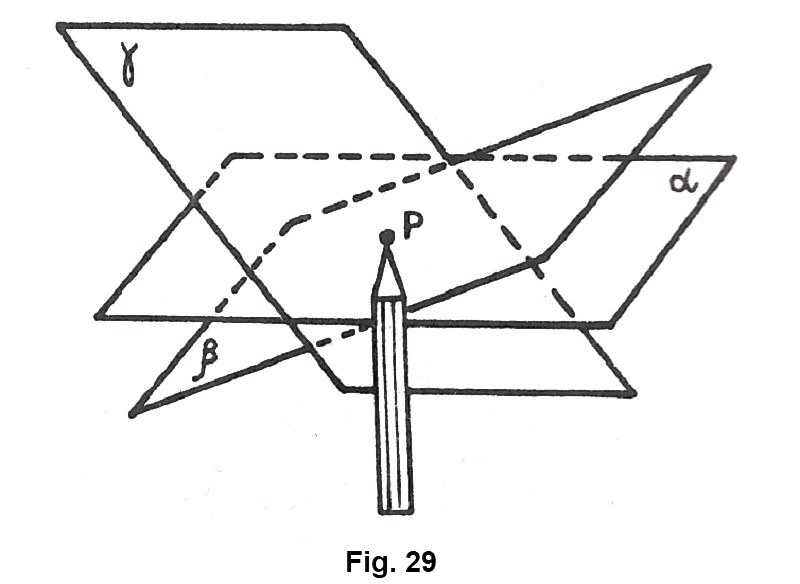
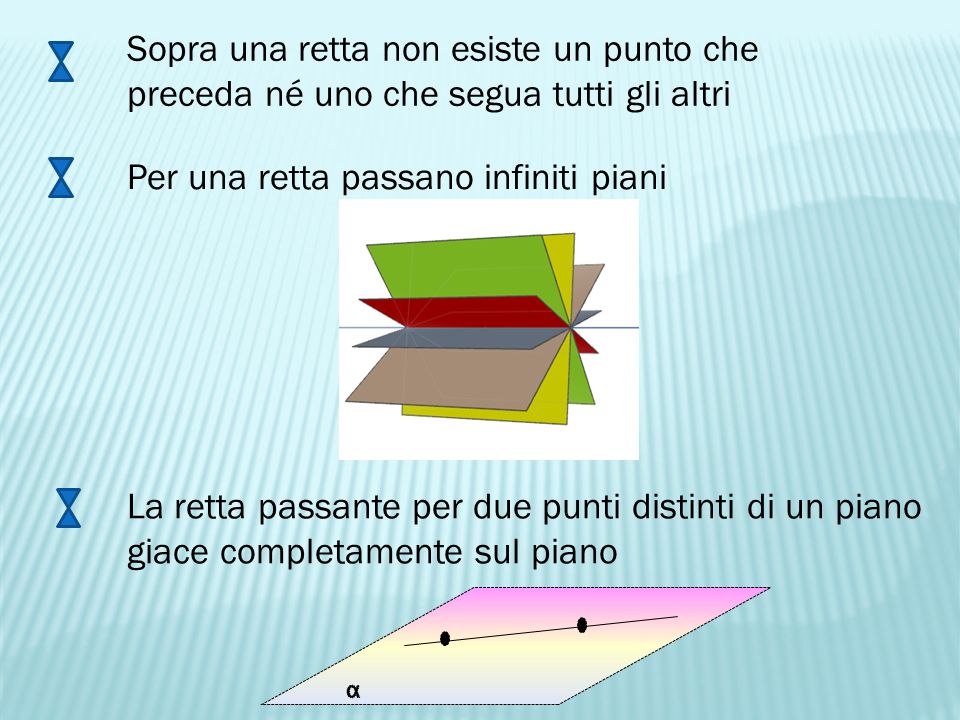
Per Una Retta Passano Infiniti Piani

Capita a tutti, a volte, di sentirsi un po' persi di fronte alla geometria. Concetti come "retta" e "piano" possono sembrare astratti e difficili da visualizzare. Ma non preoccuparti! La matematica è come un linguaggio: una volta imparate le regole, tutto diventa più chiaro. Oggi, esploreremo un'idea fondamentale: per una retta passano infiniti piani. Cercheremo di capire cosa significa, perché è vero e come visualizzarlo.

Comprendere il Concetto: Un Viaggio Visivo

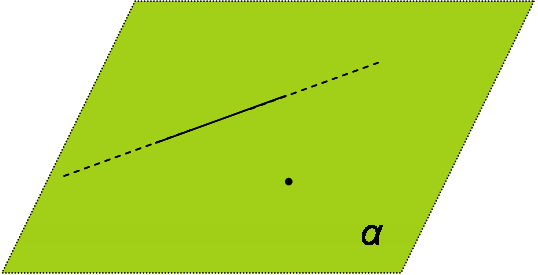
Immagina di tenere in mano una bacchetta, un semplice bastoncino. Questa bacchetta rappresenta la nostra retta. Ora, prendi un foglio di carta: questo è un piano. Prova a far passare il foglio di carta attraverso la bacchetta. Noterai subito che puoi farlo in moltissimi modi. Puoi inclinare il foglio su e giù, a destra e a sinistra, e in ogni posizione il foglio (il piano) conterrà sempre la bacchetta (la retta).

Questo è il nocciolo della questione: un'unica retta può far parte di innumerevoli piani. Ogni foglio di carta, in ogni possibile inclinazione, rappresenta un piano diverso che contiene la retta. Questo "innumerevoli" in matematica lo chiamiamo infinito. Quindi, per una retta passano infiniti piani.

Perché è Vero? Un Approccio Matematico Semplice

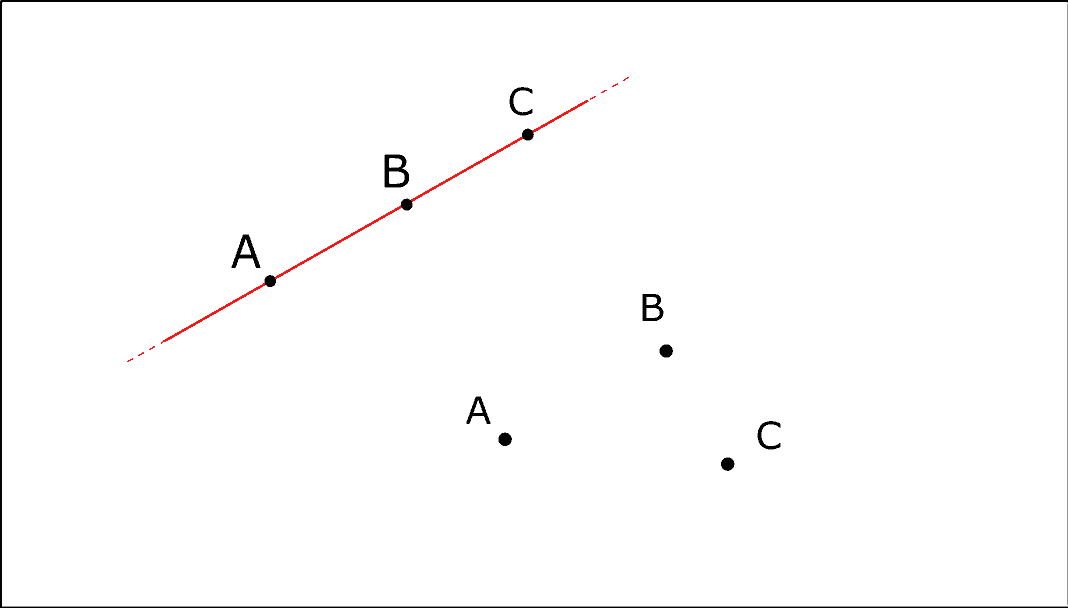
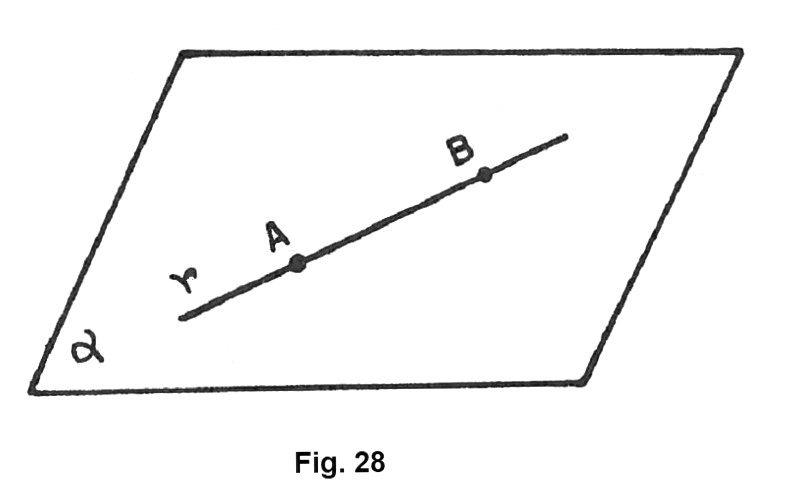
Cerchiamo di capire meglio perché questo accade. Un piano è definito da tre punti non allineati. Cosa significa? Immagina di avere tre puntini su un foglio. Se questi tre puntini non si trovano sulla stessa linea retta, allora esiste un unico piano che li contiene tutti e tre.

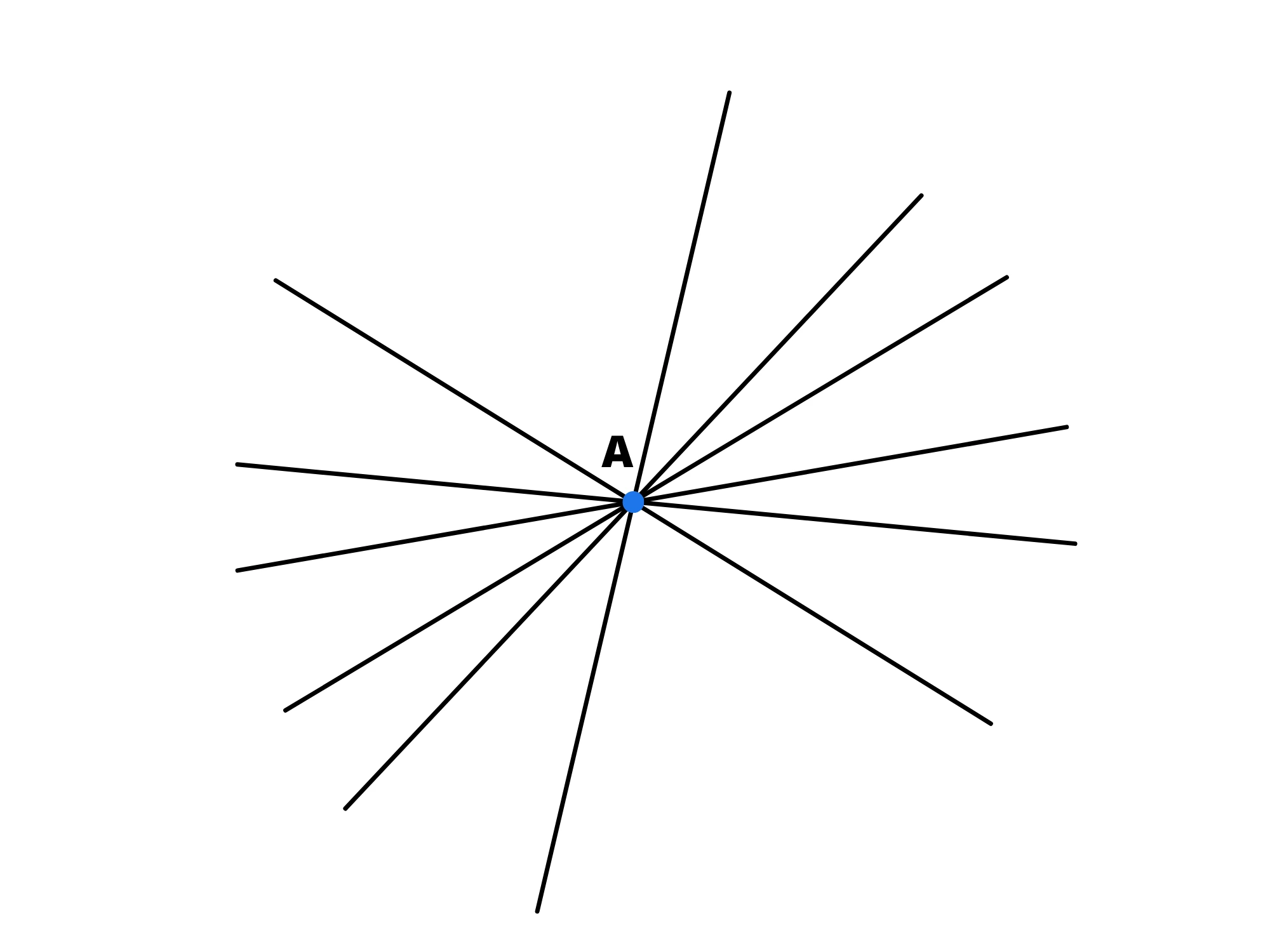
Ora, considera la nostra retta. Per definire un piano che contenga questa retta, abbiamo bisogno di un terzo punto. Questo terzo punto non deve trovarsi sulla retta. Ma quanti punti possiamo scegliere che non si trovino sulla retta? Infiniti! Ogni punto che scegliamo, combinato con la retta, definisce un piano diverso. Dato che ci sono infiniti punti fuori dalla retta, ci sono infiniti piani che la contengono.

L'Importanza nella Geometria e Oltre

Questo concetto non è solo un esercizio teorico. Ha delle implicazioni importanti nella geometria nello spazio e in altre aree della matematica e della fisica. Ad esempio, quando studiamo le relazioni tra rette e piani nello spazio tridimensionale, questa idea diventa cruciale. Ci aiuta a capire come gli oggetti si posizionano e interagiscono tra loro.

Inoltre, il concetto di infinito è fondamentale in matematica. Capire che qualcosa può essere infinito, come il numero di piani che passano per una retta, ci apre la mente a nuove possibilità e ci aiuta a pensare in modo più astratto.

Esempio Pratico: La Cerniera di una Porta

Un esempio pratico che possiamo trovare nella vita di tutti i giorni è la cerniera di una porta. La cerniera rappresenta la retta. La porta, quando si apre e si chiude, descrive diversi piani che contengono la retta (la cerniera). Ogni posizione della porta corrisponde a un piano diverso. Anche se la porta non può assumere infinite posizioni, questo esempio ci aiuta a visualizzare come una retta può appartenere a molti piani diversi.

Consigli Pratici per Studenti, Insegnanti e Genitori

Ecco alcuni consigli pratici per affrontare questo concetto in modo efficace:

Per gli studenti: Non aver paura di sperimentare! Usa oggetti fisici come bacchette e fogli di carta per visualizzare la retta e i piani. Disegna, costruisci modelli e cerca esempi nella vita di tutti i giorni. Ricorda, la pratica rende perfetti!
Per gli insegnanti: Rendete le lezioni interattive e coinvolgenti. Utilizzate dimostrazioni pratiche, software di geometria dinamica e discussioni di gruppo. Incoraggiate gli studenti a porre domande e a esplorare il concetto in modo creativo. Enfatizzate l'importanza di visualizzare i concetti geometrici.
Per i genitori: Supportate i vostri figli nel loro percorso di apprendimento. Fornite loro materiali di studio, aiutateli a fare i compiti e incoraggiateli a pensare in modo critico. Mostrate loro come la matematica è presente nella vita di tutti i giorni. Un ambiente di apprendimento positivo può fare la differenza!

Superare le Difficoltà: Visualizzazione e Analogie

Alcune delle difficoltà più comuni che gli studenti incontrano con questo concetto includono:

Difficoltà di visualizzazione: Molti studenti faticano a immaginare i piani che passano per una retta. Incoraggiare l'uso di modelli fisici e software di geometria può essere molto utile.
Confusione tra retta e piano: È importante sottolineare la differenza tra una retta (un oggetto unidimensionale) e un piano (un oggetto bidimensionale).
Astrazione del concetto di infinito: Il concetto di infinito può essere difficile da comprendere. Utilizzare esempi concreti e analogie può aiutare a rendere l'idea più accessibile.

Non scoraggiarti se all'inizio sembra difficile! La geometria richiede tempo e pratica. Continua a esplorare, a sperimentare e a porre domande. Con un po' di impegno, sarai in grado di padroneggiare questo concetto e molti altri.

Conclusione: Un Invito all'Esplorazione

L'affermazione "per una retta passano infiniti piani" è un tassello fondamentale nel puzzle della geometria. Comprendere questo concetto non solo ti aiuterà a risolvere problemi, ma ti aprirà la mente a un modo nuovo di pensare allo spazio che ci circonda. Ricorda, la matematica non è solo un insieme di regole e formule, ma un modo per esplorare e comprendere il mondo. Quindi, continua a esplorare, a imparare e a scoprire le meraviglie della geometria!

L'apprendimento è un viaggio, non una destinazione. Goditi il percorso e non aver paura di chiedere aiuto quando ne hai bisogno. Con la giusta guida e un po' di impegno, puoi raggiungere traguardi che non avresti mai immaginato.