Parabola Con Concavità Verso Il Basso

Ti sei mai trovato a fissare un grafico, cercando di capire se quella curva sorridente o imbronciata avesse un significato per la tua vita? Molte volte ci sentiamo spaesati di fronte alla matematica, ma la verità è che le parabole, con la loro forma elegante e le loro proprietà affascinanti, sono ovunque intorno a noi. Oggi ci concentreremo su un tipo specifico di parabola: quella con la concavità verso il basso. Capire come funziona può darti strumenti preziosi per interpretare il mondo.

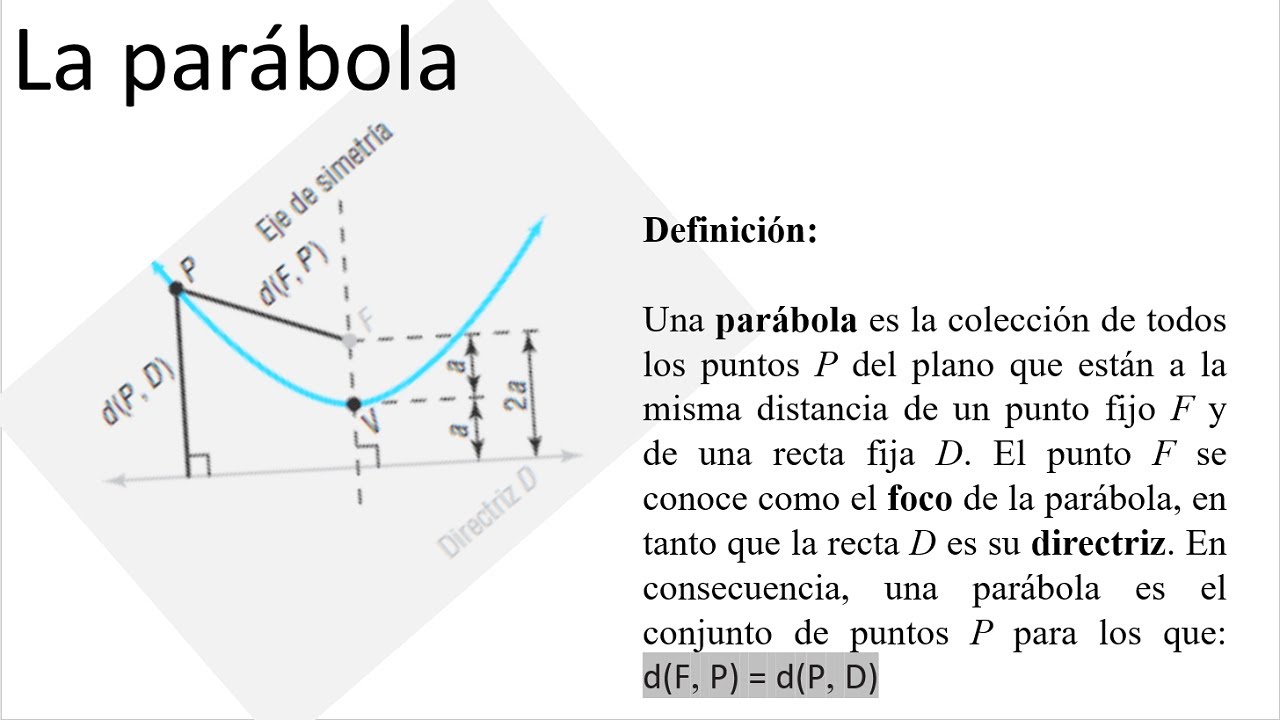
Cos'è una Parabola con Concavità Verso il Basso?

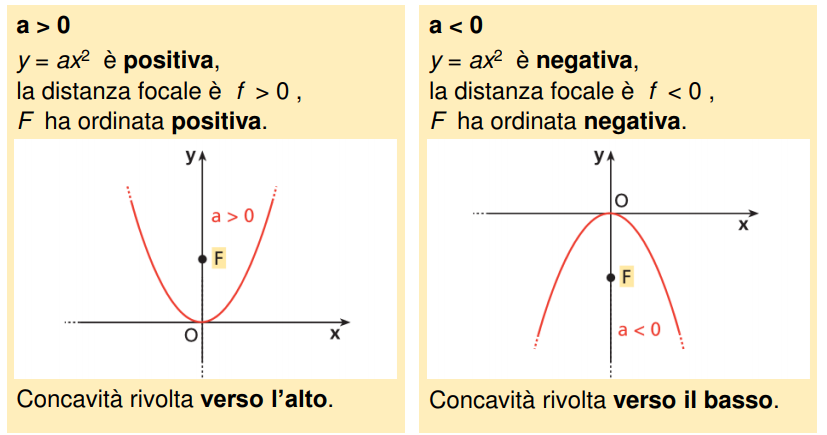
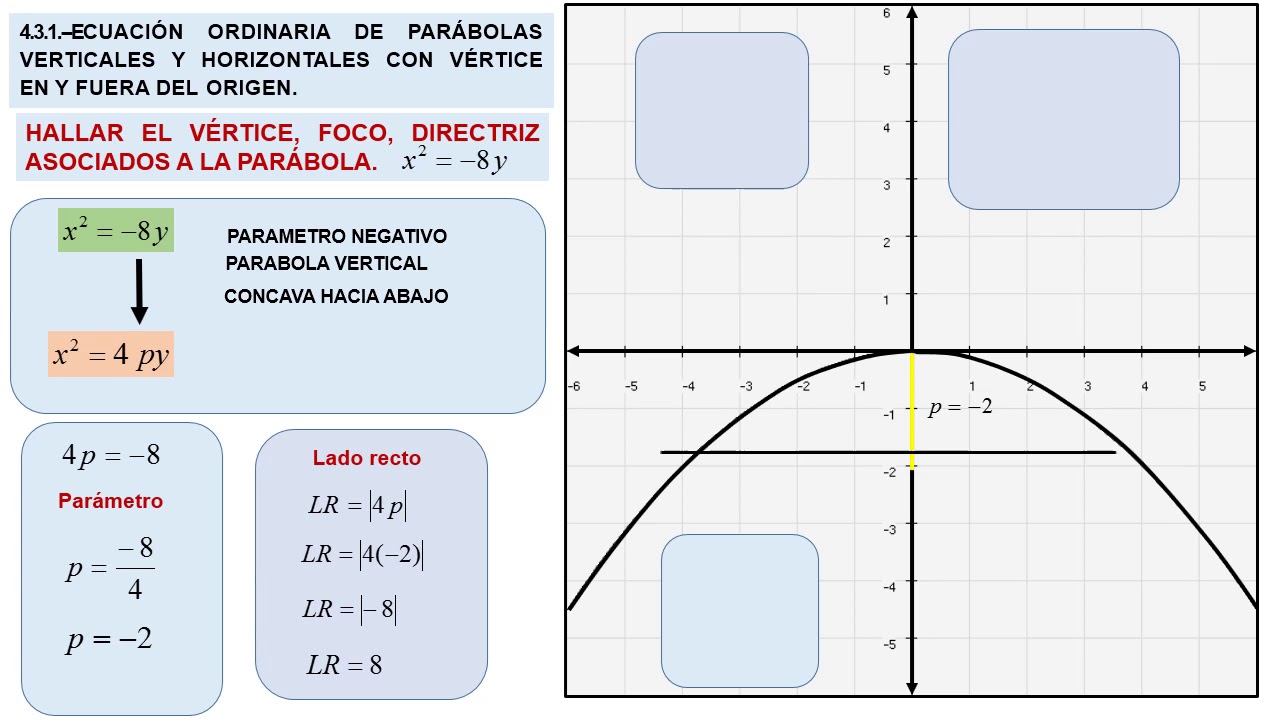
Immagina una U rovesciata, oppure l'arco che disegna una fontana che spruzza acqua verso l'alto prima di ricadere. Ecco, quella è una parabola con concavità verso il basso. In termini matematici, è una curva definita da un'equazione quadratica nella forma generale: y = ax² + bx + c. La chiave per determinare se la concavità è verso il basso risiede nel coefficiente "a".

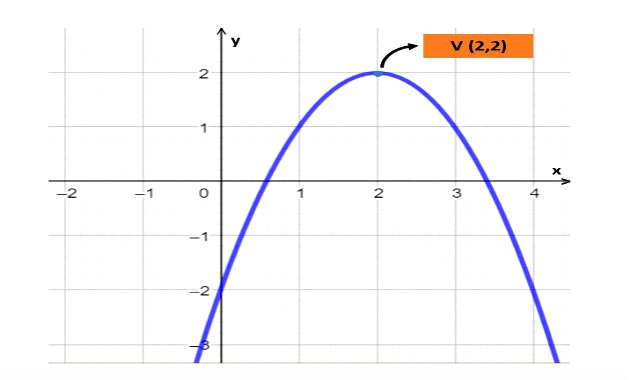
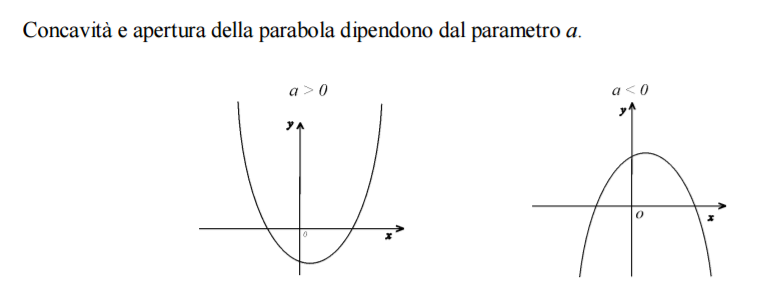
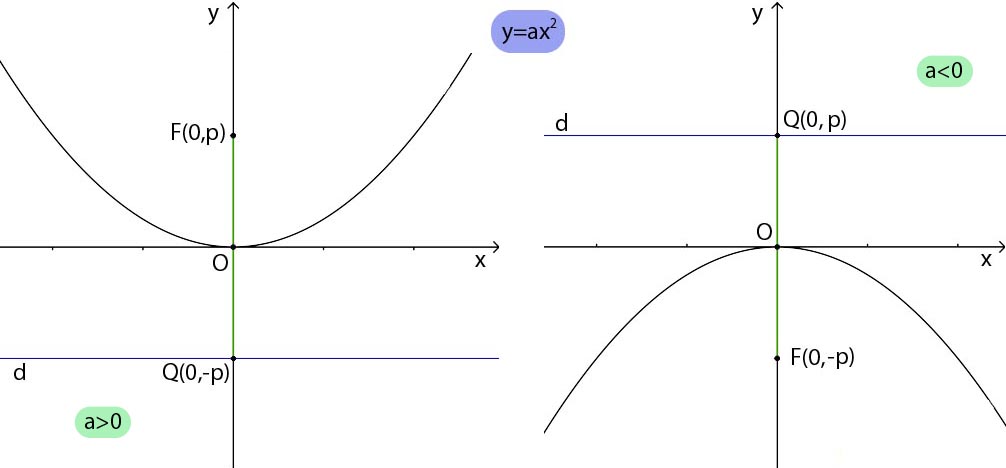
Se a < 0 (ovvero, "a" è un numero negativo), allora la parabola ha concavità verso il basso. Questo significa che la curva si apre verso il basso, come una coppa capovolta. Il punto più alto della parabola, chiamato vertice, rappresenta il valore massimo della funzione.

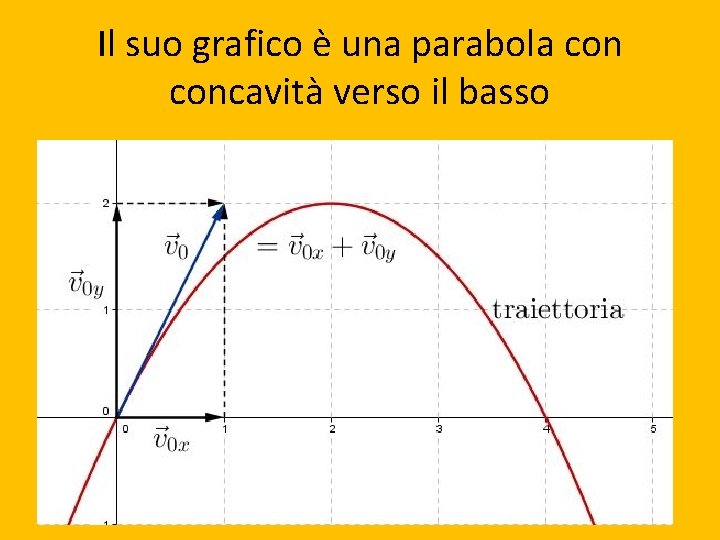
Un Esempio Pratico: Pensa al lancio di un pallone da basket. La traiettoria del pallone descrive approssimativamente una parabola con concavità verso il basso. Il vertice rappresenta l'altezza massima raggiunta dal pallone, e i punti in cui la parabola interseca il suolo (se ci sono) rappresentano il momento in cui il pallone viene lanciato e quando tocca terra.

Perché è Importante Capire le Parabole con Concavità Verso il Basso?

La comprensione delle parabole con concavità verso il basso non è solo un esercizio accademico; ha applicazioni pratiche in una vasta gamma di discipline:

• Fisica: Come abbiamo visto con il pallone da basket, le parabole descrivono la traiettoria dei proiettili, permettendo di calcolare la gittata, l'altezza massima e il tempo di volo.
• Economia: Le curve di profitto spesso assumono una forma parabolica con concavità verso il basso. Il vertice rappresenta il punto di massimo profitto che un'azienda può ottenere.
• Ingegneria: Nella progettazione di ponti, antenne paraboliche e strutture architettoniche, la forma parabolica garantisce una distribuzione ottimale delle forze e la massima resistenza strutturale.
• Statistica: In alcune analisi di regressione, la relazione tra due variabili può essere approssimata da una parabola.

Quindi, imparare a riconoscere e interpretare le parabole con concavità verso il basso può fornirti una prospettiva più profonda su una varietà di fenomeni del mondo reale.

Come Identificare una Parabola con Concavità Verso il Basso

Ecco alcuni consigli pratici per identificare una parabola con concavità verso il basso, sia da un'equazione che da un grafico:

Dall'Equazione:

1. Controlla il coefficiente di x²: Come abbiamo detto, se il coefficiente "a" in y = ax² + bx + c è negativo, la parabola ha concavità verso il basso.
2. Non farti ingannare dagli altri termini: I coefficienti "b" e "c" influenzano la posizione del vertice e l'intersezione con l'asse y, ma non la concavità.

Dal Grafico:

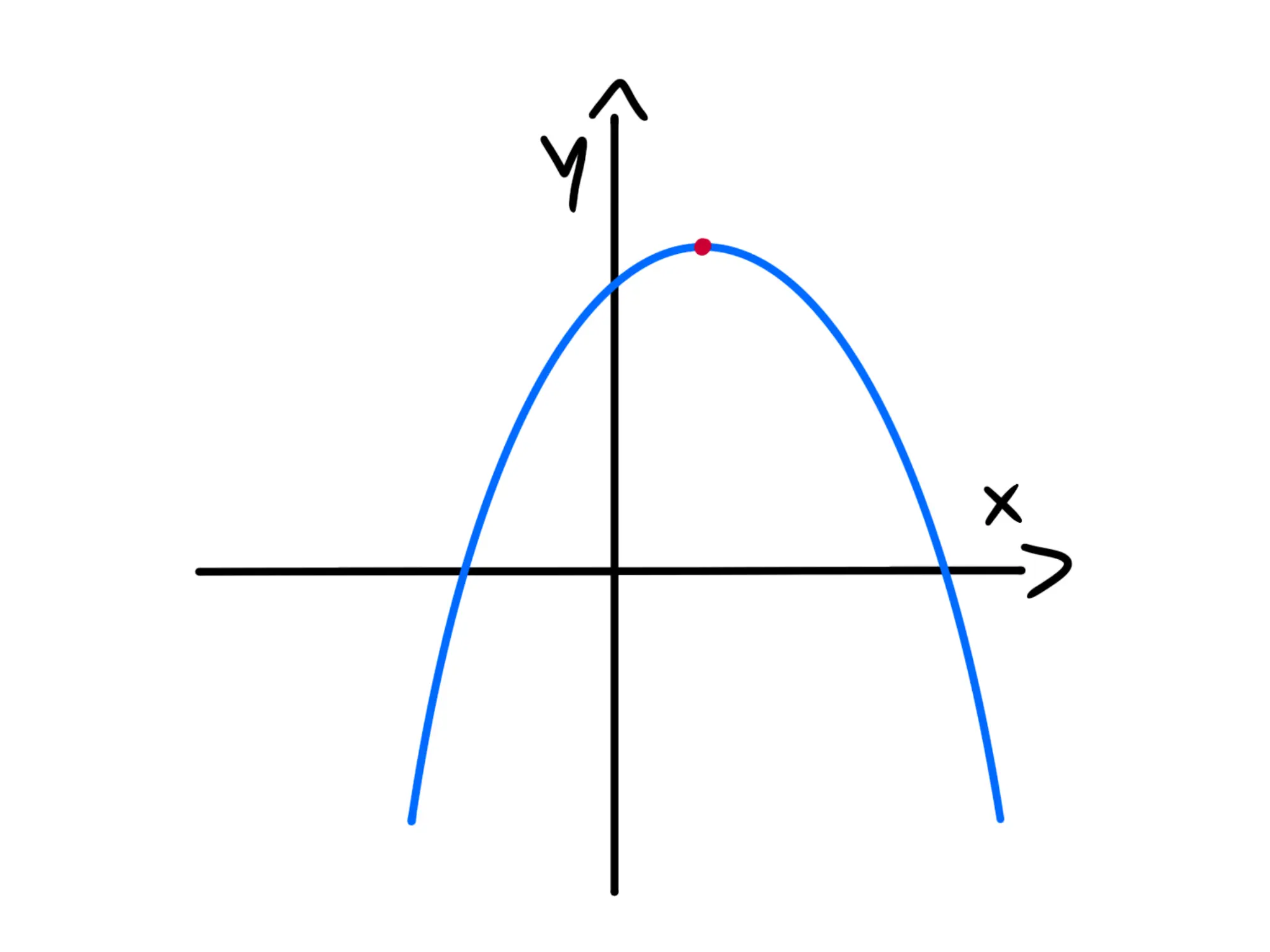
1. Osserva la direzione della curva: Se la curva si apre verso il basso, allora è una parabola con concavità verso il basso.
2. Individua il vertice: Il vertice è il punto più alto della curva.
3. Immagina una "U" rovesciata: Se la forma della curva assomiglia a una "U" rovesciata, allora è molto probabile che sia una parabola con concavità verso il basso.

Calcolare il Vertice di una Parabola con Concavità Verso il Basso

Il vertice è un punto fondamentale di una parabola. Per una parabola con concavità verso il basso, rappresenta il valore massimo della funzione. Le coordinate del vertice (x_v, y_v) possono essere calcolate usando le seguenti formule:

• x_v = -b / 2a
• y_v = f(x_v) = a(x_v)² + b(x_v) + c

In pratica, si calcola prima la coordinata x del vertice usando la prima formula, e poi si sostituisce questo valore nell'equazione della parabola per trovare la coordinata y del vertice.

Esempio: Consideriamo la parabola definita dall'equazione y = -2x² + 8x - 3. In questo caso, a = -2, b = 8, e c = -3. Calcoliamo il vertice:

• x_v = -8 / (2 * -2) = -8 / -4 = 2
• y_v = -2(2)² + 8(2) - 3 = -2(4) + 16 - 3 = -8 + 16 - 3 = 5

Quindi, il vertice della parabola è (2, 5). Questo significa che il valore massimo della funzione è 5, e si verifica quando x = 2.

Esercizi Pratici

Per consolidare la tua comprensione delle parabole con concavità verso il basso, prova a risolvere questi esercizi:

1. Identifica la concavità: Per ciascuna delle seguenti equazioni, determina se la parabola ha concavità verso l'alto o verso il basso:
   • y = 3x² - 5x + 2
   • y = -x² + 4x - 1
   • y = -0.5x² + x + 3
   • y = 2x² + 7x - 4
2. Calcola il vertice: Per le parabole con concavità verso il basso degli esercizi precedenti, calcola le coordinate del vertice.
3. Problema di applicazione: Un'azienda produce un certo prodotto. La funzione di profitto è data da P(x) = -x² + 100x - 1000, dove x rappresenta il numero di unità prodotte. Determina il numero di unità che l'azienda deve produrre per massimizzare il profitto e qual è il profitto massimo.

Conclusione

Le parabole con concavità verso il basso sono molto più di semplici curve matematiche. Sono strumenti potenti che ci aiutano a modellare e comprendere una vasta gamma di fenomeni del mondo reale. Imparando a identificarle, analizzarle e utilizzarle, puoi acquisire una comprensione più profonda del mondo che ti circonda. Non aver paura di sperimentare con diverse equazioni e grafici per affinare le tue abilità. La matematica, dopotutto, è un linguaggio che ci permette di decifrare i segreti dell'universo.