Numeratore E Denominatore Di Una Frazione

Una frazione rappresenta una parte di un intero. È un concetto fondamentale in matematica e si compone di due elementi chiave: il numeratore e il denominatore. Comprendere il ruolo e il significato di entrambi è essenziale per padroneggiare le frazioni e le loro applicazioni.

Il Numeratore: Cosa Indica

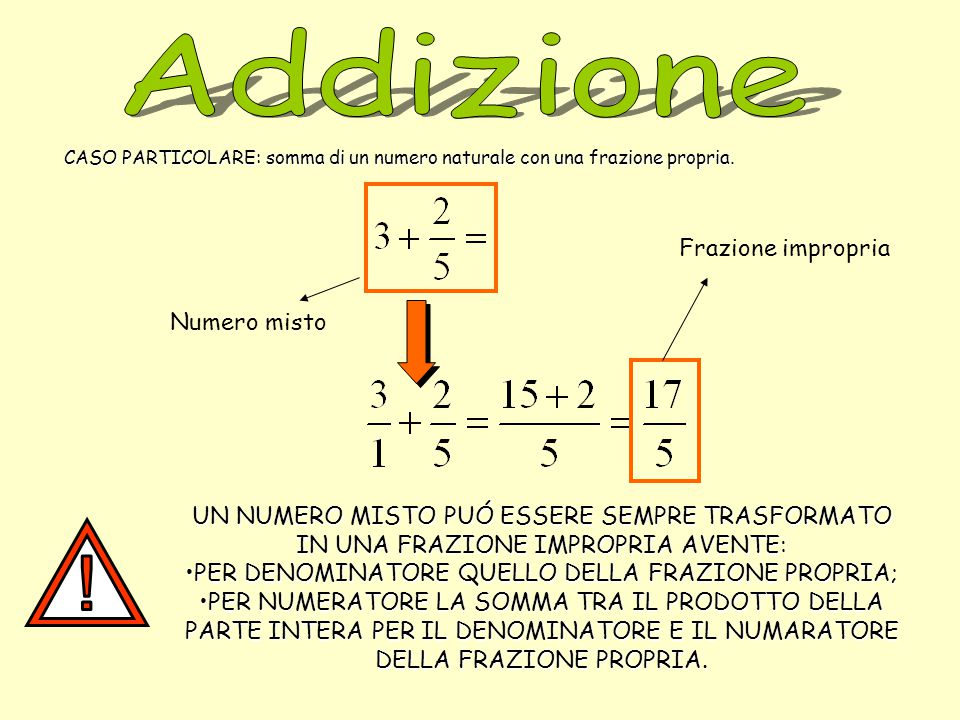
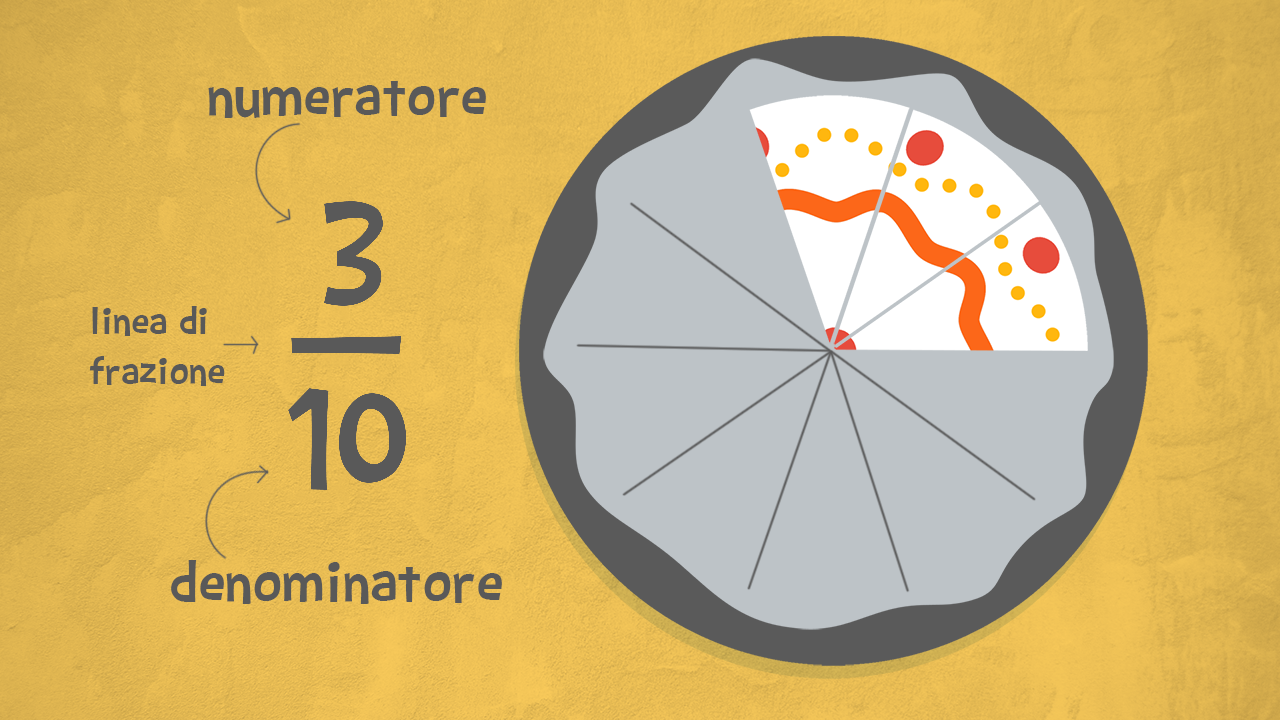
Il numeratore è il numero che si trova sopra la linea di frazione. Indica quante parti dell'intero stiamo considerando. Ad esempio, nella frazione 3/4, il 3 è il numeratore. Significa che abbiamo preso in considerazione 3 parti di un intero che è stato diviso in 4 parti uguali.

Perché il Numeratore è Importante

Il numeratore è cruciale perché determina la quantità rappresentata dalla frazione. Senza il numeratore, non possiamo sapere quante parti stiamo prendendo in considerazione. Un cambio nel numeratore altera direttamente il valore della frazione. Se, ad esempio, passiamo da 3/4 a 1/4, la quantità considerata diminuisce significativamente.

Diversi studi pedagogici evidenziano come la comprensione intuitiva del numeratore sia un predittore della capacità di risolvere problemi più complessi con le frazioni.

"La comprensione concettuale del numeratore come indicatore della quantità presa è fondamentale per l'operatività con le frazioni,"

Il Denominatore: La Dimensione delle Parti

Il denominatore è il numero che si trova sotto la linea di frazione. Indica in quante parti uguali è stato diviso l'intero. Nella frazione 3/4, il 4 è il denominatore. Significa che l'intero è stato diviso in 4 parti uguali.

Perché il Denominatore è Importante

Il denominatore definisce la dimensione delle parti in cui è stato diviso l'intero. Un denominatore più grande significa che l'intero è stato diviso in più parti, e quindi ogni parte è più piccola. Un denominatore più piccolo significa che l'intero è stato diviso in meno parti, e quindi ogni parte è più grande. La comprensione del denominatore è fondamentale per confrontare frazioni e eseguire operazioni con esse.

Come afferma il Dott. Luca Bianchi, autore di diversi libri di testo per la scuola secondaria:

"La relazione tra numeratore e denominatore è ciò che definisce il valore di una frazione. Un denominatore che cambia influisce drasticamente sul significato della frazione."

Applicazioni Pratiche nella Vita Scolastica e Quotidiana

La comprensione di numeratore e denominatore non è solo teorica, ma ha applicazioni pratiche nella vita quotidiana degli studenti. Ecco alcuni esempi:

• Condivisione di una pizza: Se una pizza è divisa in 8 fette (denominatore = 8) e tu ne mangi 3 (numeratore = 3), hai mangiato 3/8 della pizza.
• Dividere una torta di compleanno: Se una torta è divisa in 12 fette e ci sono 6 invitati, ogni invitato riceverà 6/12 della torta, che può essere semplificata a 1/2.
• Calcolare una percentuale: Le percentuali sono frazioni con denominatore 100. Se ottieni un voto di 85/100 a un esame, hai ottenuto l'85%.

In ambito scolastico, la conoscenza di numeratore e denominatore è fondamentale per:

• Risolvere problemi di proporzionalità.
• Calcolare probabilità.
• Comprendere concetti di geometria, come le aree e i volumi.

In conclusione, numeratore e denominatore sono i due pilastri su cui si basa il concetto di frazione. Una solida comprensione di entrambi è essenziale per il successo in matematica e per affrontare problemi pratici nella vita di tutti i giorni. Insegnanti e genitori dovrebbero enfatizzare l'importanza di una comprensione concettuale, andando oltre la semplice memorizzazione di regole e procedure.