Misura Degli Angoli Di Un Triangolo Isoscele

Quante volte ti sei trovato di fronte a un problema di geometria che sembrava insormontabile? Magari un triangolo isoscele con angoli misteriosi da scoprire... Non sei solo! Molti studenti si sentono persi quando si tratta di misurare gli angoli in queste figure geometriche. Ma non temere, con un po' di pazienza e le giuste strategie, diventerai un esperto!

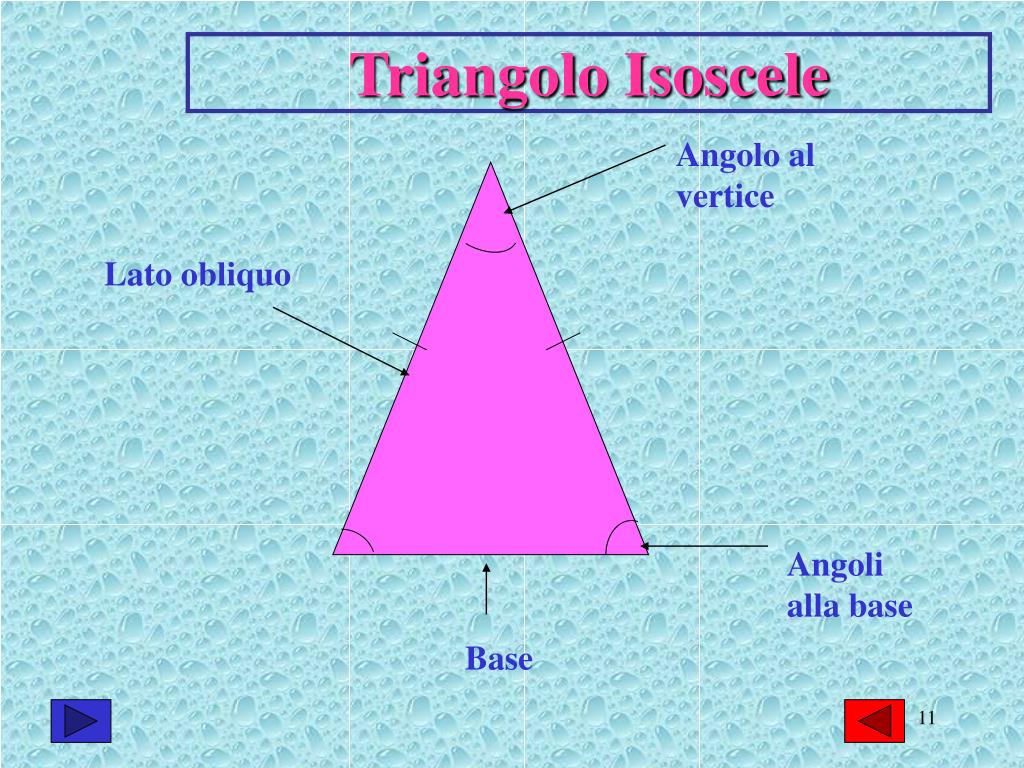
Comprendere il Triangolo Isoscele: Le Basi

Innanzitutto, facciamo un passo indietro e definiamo cosa intendiamo per triangolo isoscele. Un triangolo isoscele è un triangolo che ha due lati uguali. Questa proprietà fondamentale è la chiave per sbloccare i segreti dei suoi angoli.

Proprietà Chiave:

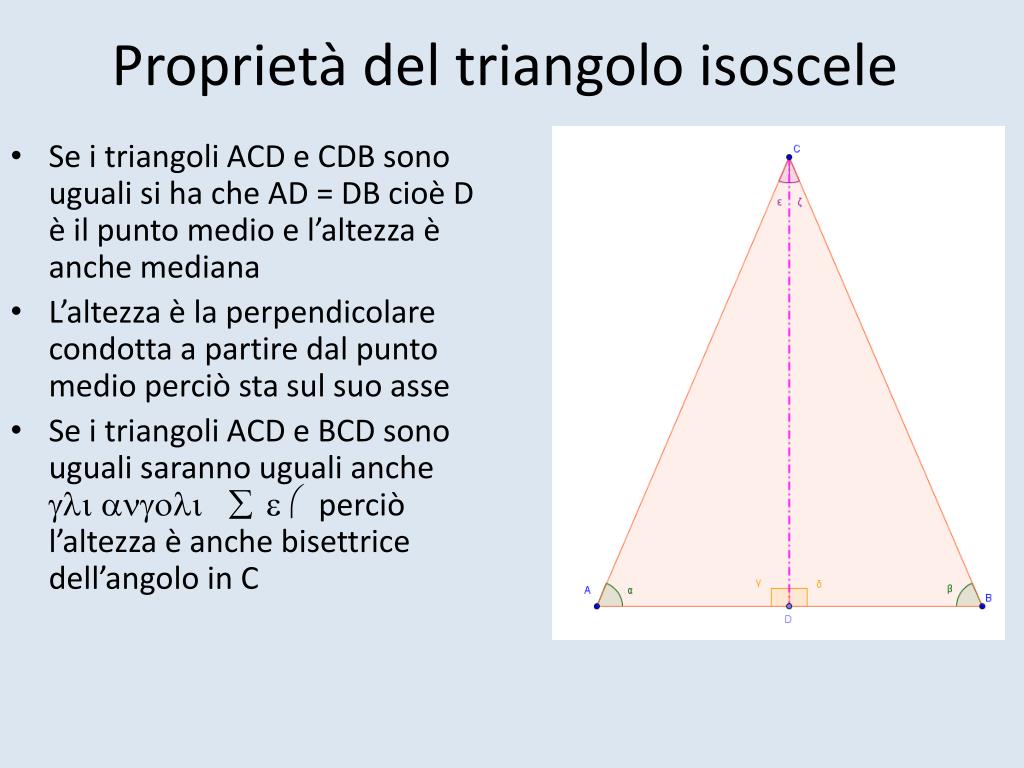
Ha due lati congruenti (uguali).
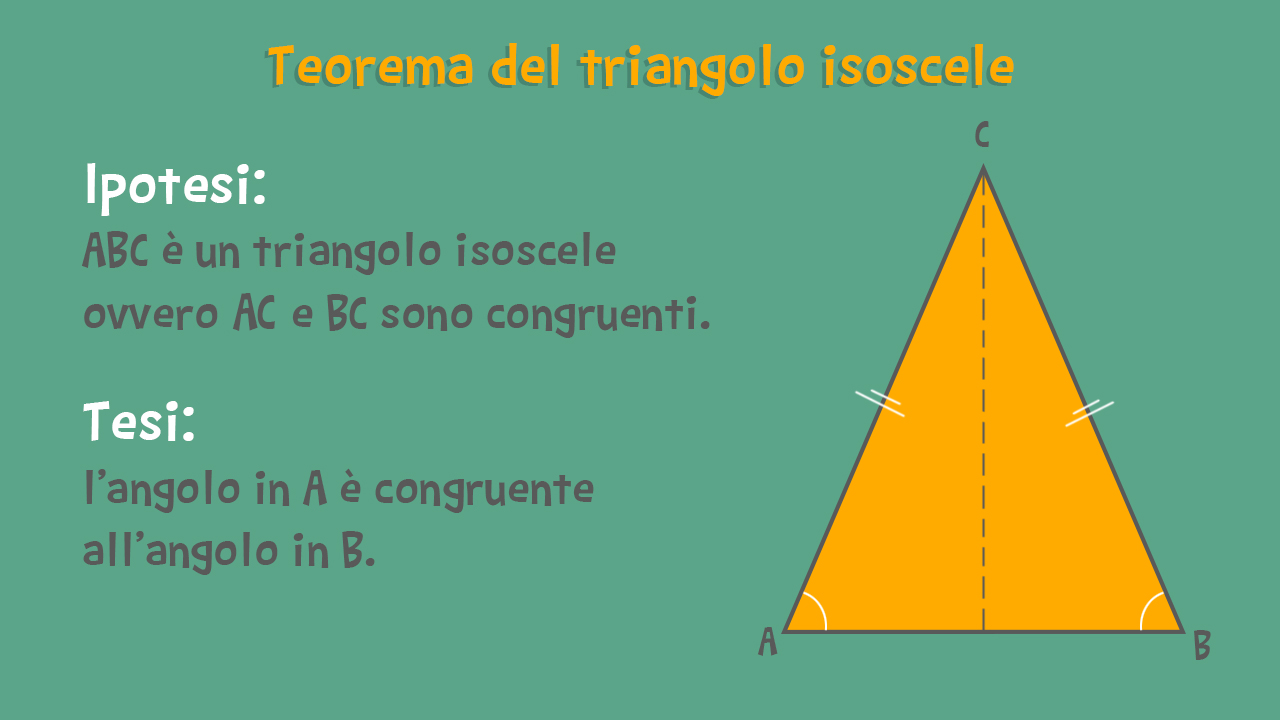
Ha due angoli alla base congruenti (uguali).

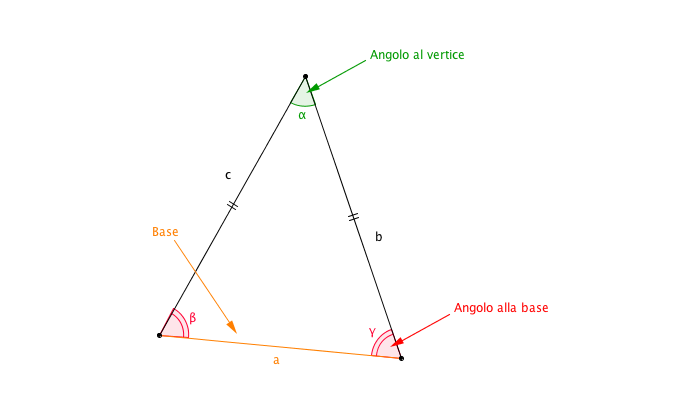
Questi angoli congruenti sono opposti ai lati congruenti e si chiamano angoli alla base. L'angolo restante, quello opposto alla base (il lato non congruente), si chiama angolo al vertice.

Come afferma la prof.ssa Maria Rossi, autrice di "Geometria Facile per Tutti" (2020), "La congruenza dei lati in un triangolo isoscele implica una specifica relazione tra i suoi angoli, che rende i calcoli più semplici rispetto ai triangoli scaleni."

Il Teorema Fondamentale: La Somma degli Angoli Interni

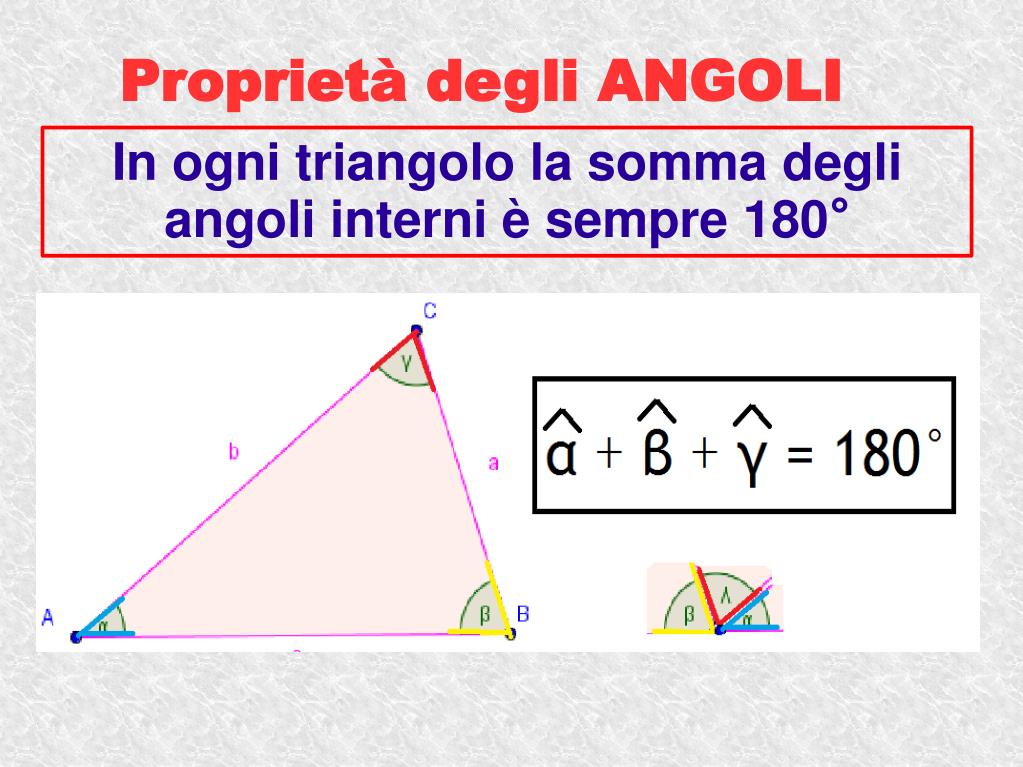
Prima di immergerci nei calcoli specifici per il triangolo isoscele, dobbiamo ricordare un teorema cruciale: la somma degli angoli interni di un qualsiasi triangolo è sempre 180 gradi. Questa è una verità assoluta della geometria euclidea!

Matematicamente: α + β + γ = 180°, dove α, β e γ rappresentano le misure dei tre angoli del triangolo.

Questo teorema è il nostro punto di partenza per risolvere quasi tutti i problemi di geometria riguardanti gli angoli.

Misurare gli Angoli: Metodo Passo-Passo

Ora che abbiamo le basi, vediamo come misurare gli angoli di un triangolo isoscele, considerando diversi scenari:

Scenario 1: Conosciamo l'Angolo al Vertice

Se conosciamo la misura dell'angolo al vertice (chiamiamolo γ), possiamo trovare gli angoli alla base (α e β, che sono uguali) usando la seguente formula:

α = β = (180° - γ) / 2

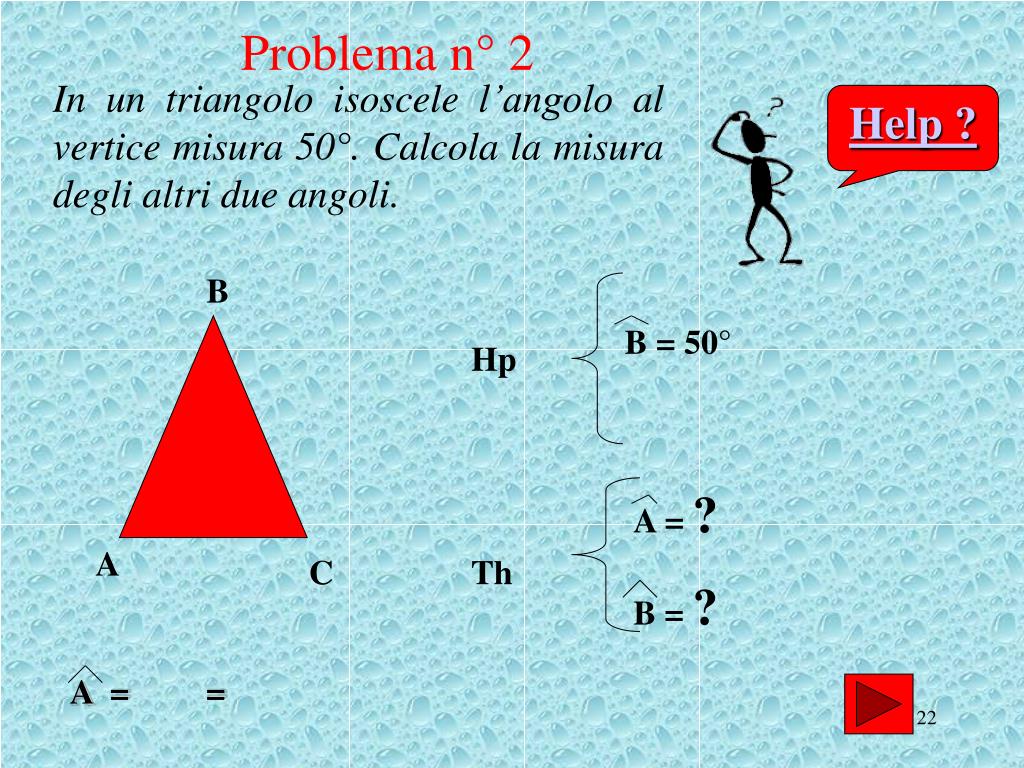
Esempio: Se l'angolo al vertice è di 50°, allora:

α = β = (180° - 50°) / 2 = 130° / 2 = 65°

Quindi, ogni angolo alla base misura 65°.

Scenario 2: Conosciamo un Angolo alla Base

Se conosciamo la misura di un angolo alla base (α o β), sappiamo automaticamente anche la misura dell'altro angolo alla base, perché sono uguali. Per trovare l'angolo al vertice (γ), usiamo la seguente formula:

γ = 180° - 2α (se conosciamo α) oppure γ = 180° - 2β (se conosciamo β)

Esempio: Se un angolo alla base è di 70°, allora:

γ = 180° - 2 * 70° = 180° - 140° = 40°

Quindi, l'angolo al vertice misura 40°.

Scenario 3: Conosciamo il Rapporto tra gli Angoli

A volte, il problema non ci fornisce direttamente la misura di un angolo, ma ci dà informazioni sul rapporto tra gli angoli. Ad esempio, potrebbe dirci che l'angolo al vertice è il doppio di un angolo alla base.

Esempio: L'angolo al vertice è il doppio di un angolo alla base. Quindi, γ = 2α. Utilizzando il teorema sulla somma degli angoli interni, abbiamo:

α + α + 2α = 180°

4α = 180°

α = 45°

Quindi, gli angoli alla base misurano 45° ciascuno, e l'angolo al vertice misura 2 * 45° = 90°.

Strumenti Utili per Misurare gli Angoli

Per misurare gli angoli in modo preciso, possiamo utilizzare diversi strumenti:

Goniometro: Lo strumento classico per misurare gli angoli. Assicurati di posizionare correttamente il centro del goniometro sul vertice dell'angolo e allineare uno dei lati dell'angolo con lo zero.
Software di Geometria Dinamica (es. GeoGebra): Questi software permettono di disegnare triangoli, misurare angoli e manipolare le figure per esplorare le loro proprietà. Sono particolarmente utili per visualizzare concetti astratti.
App per Smartphone: Esistono diverse app che utilizzano la fotocamera dello smartphone per misurare gli angoli in tempo reale. Sono un'alternativa comoda al goniometro tradizionale.

Secondo uno studio condotto dall'Università di Pisa (2018) sull'efficacia dell'utilizzo di software di geometria dinamica nell'apprendimento della geometria, gli studenti che utilizzano questi strumenti mostrano un miglioramento significativo nella comprensione dei concetti geometrici e nelle capacità di risoluzione dei problemi.

Consigli Pratici e Trucchi

Disegna sempre un diagramma: Un disegno chiaro e preciso del triangolo isoscele ti aiuterà a visualizzare il problema e a identificare le relazioni tra gli angoli.
Scrivi le formule: Annota le formule che utilizzi per evitare errori.
Verifica la tua risposta: Assicurati che la somma degli angoli che hai calcolato sia uguale a 180°.
Esercitati regolarmente: La pratica è fondamentale per acquisire sicurezza e padronanza nella risoluzione dei problemi di geometria.
Non aver paura di chiedere aiuto: Se ti blocchi, chiedi aiuto al tuo insegnante, ai tuoi compagni di classe o consulta risorse online.

Esercizi per Mettere in Pratica le Tue Conoscenze

Ecco alcuni esercizi per mettere alla prova le tue abilità:

Un triangolo isoscele ha un angolo al vertice di 80°. Qual è la misura degli angoli alla base?
Un angolo alla base di un triangolo isoscele misura 65°. Qual è la misura dell'angolo al vertice?
In un triangolo isoscele, l'angolo al vertice è il triplo di un angolo alla base. Trova la misura di tutti gli angoli.
Costruisci un triangolo isoscele utilizzando GeoGebra e verifica che la somma degli angoli interni sia sempre 180°.

Ricorda: La geometria è come un puzzle. Ogni pezzo ha il suo posto e, una volta che hai capito come incastrarli, tutto diventa più chiaro!

Conclusione: Geometria alla Portata di Tutti

Misurare gli angoli di un triangolo isoscele non è un compito impossibile. Con la giusta comprensione delle proprietà del triangolo, il teorema sulla somma degli angoli interni e un po' di pratica, puoi superare qualsiasi sfida geometrica. Non arrenderti mai e continua a esplorare il meraviglioso mondo della geometria!

Come diceva Galileo Galilei, "La matematica è l'alfabeto con cui Dio ha scritto l'universo." La geometria è una parte fondamentale di questo alfabeto, e impararla ti aprirà nuove prospettive sul mondo che ti circonda.