La Serie Numerica Ideata Da Un Famoso Matematico Pisano

Ti sei mai chiesto se esiste un collegamento segreto che unisce i petali di un fiore, la disposizione delle spirali in un girasole e la forma di una conchiglia? E se ti dicessi che la risposta si trova in una sequenza di numeri ideata da un matematico vissuto secoli fa? Forse hai già sentito parlare della successione di Fibonacci, ma sei consapevole del suo impatto sorprendente sul mondo che ci circonda?

La Genesi di una Sequenza Incredibile

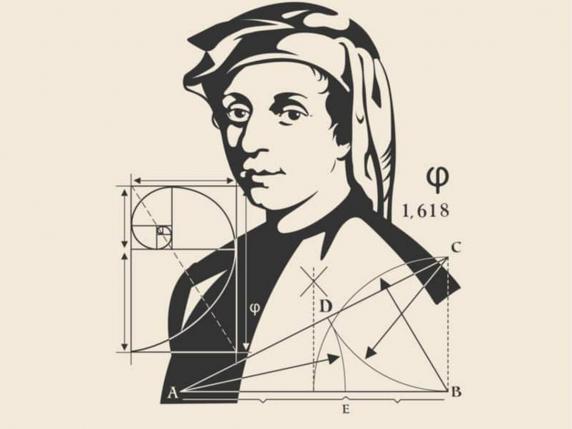
La storia di questa affascinante sequenza inizia con Leonardo Pisano, meglio conosciuto come Fibonacci, vissuto tra il XII e il XIII secolo. Sebbene sia famoso per aver introdotto in Europa il sistema numerico indo-arabico, il suo nome è indissolubilmente legato alla sequenza numerica che porta il suo nome. Nel suo libro Liber Abaci (1202), Fibonacci pose un problema riguardante la riproduzione di conigli: quanti conigli si otterrebbero in un anno, partendo da una singola coppia, se ogni coppia fertile desse alla luce una nuova coppia ogni mese, e la nuova coppia diventasse fertile a partire dal secondo mese?

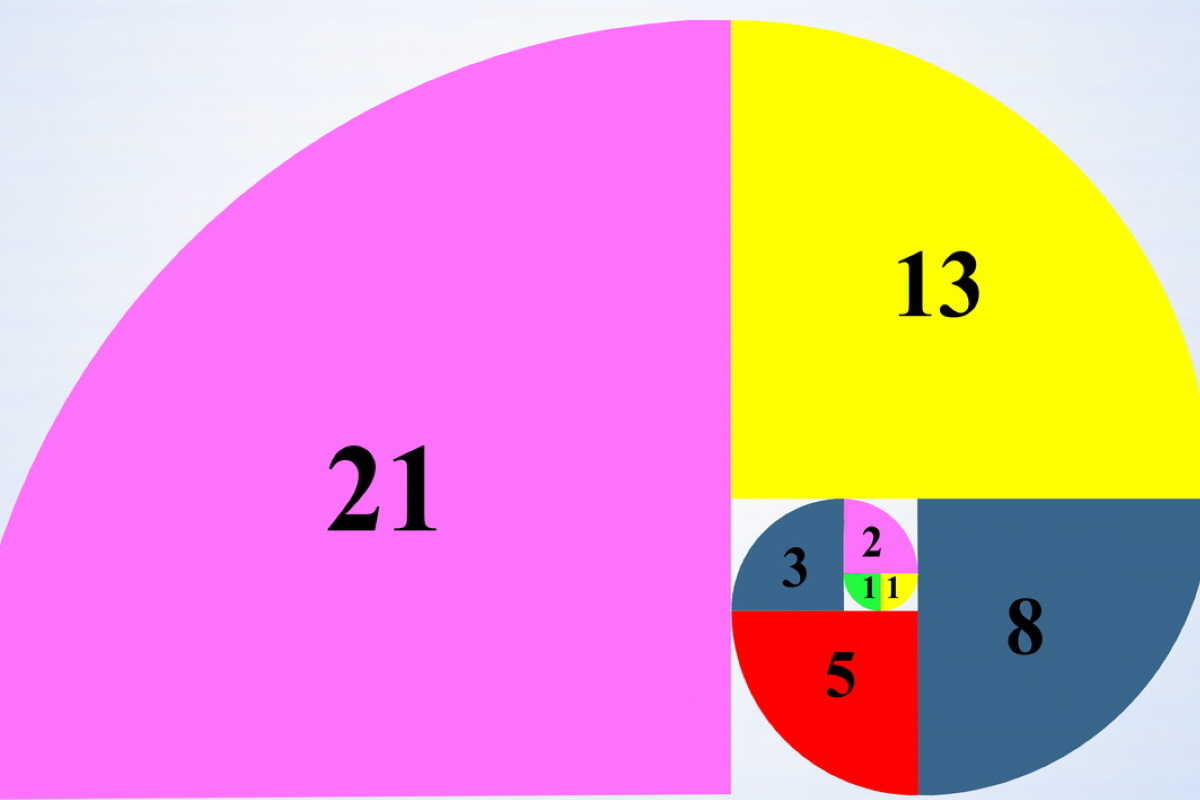
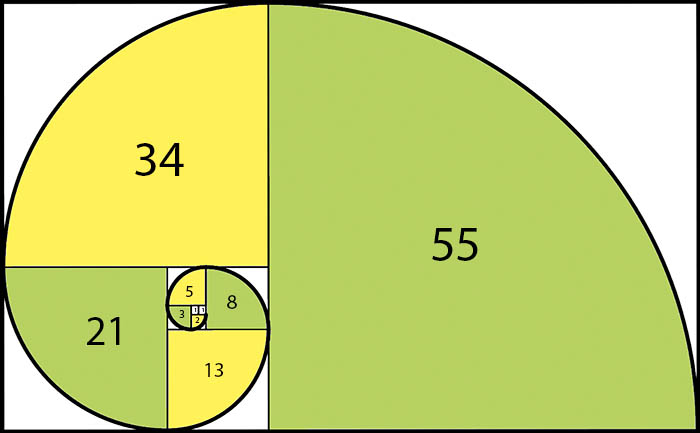
La soluzione a questo apparentemente semplice problema diede origine alla sequenza di Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... In questa sequenza, ogni numero è la somma dei due numeri precedenti. Sembra una semplice progressione aritmetica, ma le sue implicazioni vanno ben oltre l'aritmetica di base.

Come Viene Costruita la Sequenza?

La costruzione della sequenza è piuttosto semplice. Si inizia con 0 e 1. Poi, si sommano i due numeri per ottenere il successivo. Ecco come funziona:

• 0 + 1 = 1
• 1 + 1 = 2
• 1 + 2 = 3
• 2 + 3 = 5
• 3 + 5 = 8
• E così via...

Continuando questo processo, si ottiene una sequenza infinita di numeri che, come vedremo, presenta proprietà sorprendenti.

La Magia della Natura e il Numero Aureo

La vera bellezza della sequenza di Fibonacci risiede nella sua sorprendente presenza in natura. Considera il numero di spirali presenti nei girasoli: spesso troverai 34 spirali che si sviluppano in senso orario e 55 spirali in senso antiorario, entrambi numeri di Fibonacci. Lo stesso schema si ripete nelle pigne, nelle conchiglie (come il nautilus) e persino nella disposizione delle foglie su alcuni steli.

Ma cosa c'è dietro questa ricorrenza? La risposta si trova nel rapporto aureo, spesso indicato con la lettera greca phi (φ), e approssimativamente uguale a 1.618. Questo numero si ottiene dividendo un numero di Fibonacci per quello precedente. Man mano che si procede nella sequenza, il risultato di questa divisione si avvicina sempre più al rapporto aureo. Ad esempio:

• 5 / 3 = 1.666...
• 8 / 5 = 1.6
• 13 / 8 = 1.625
• 21 / 13 = 1.615...
• 34 / 21 = 1.619...

Questo rapporto aureo è considerato da molti come un principio di armonia e bellezza, e si ritiene che sia presente in molti aspetti della natura e dell'arte. La sua connessione con la sequenza di Fibonacci è uno degli aspetti più affascinanti di questa sequenza numerica.

Esempi Concreti nella Natura

Ecco alcuni esempi specifici di come la sequenza di Fibonacci e il rapporto aureo si manifestano in natura:

• Fiori: Il numero di petali di molti fiori è un numero di Fibonacci. Ad esempio, i gigli spesso hanno 3 petali, le buttercups 5, le delphiniums 8, le calendule 13, le aster 21 e così via.
• Spirali: Le spirali dei girasoli e delle pigne seguono spesso la sequenza di Fibonacci. Questo schema permette alle piante di massimizzare l'esposizione al sole e l'efficienza nell'impacchettamento dei semi.
• Conchiglie: La spirale del nautilus si avvicina a una spirale aurea, una spirale logaritmica il cui tasso di crescita è legato al rapporto aureo.
• Corpo Umano: Anche le proporzioni del corpo umano, sebbene non perfette, mostrano approssimazioni al rapporto aureo. Ad esempio, il rapporto tra l'altezza totale e la distanza dall'ombelico al piede si avvicina a φ.

Oltre la Natura: Applicazioni Moderne

L'influenza della sequenza di Fibonacci non si limita al regno naturale. Le sue proprietà uniche trovano applicazioni in vari campi, tra cui:

• Finanza: Gli analisti tecnici utilizzano i ritracciamenti di Fibonacci per identificare potenziali livelli di supporto e resistenza nei mercati finanziari. Questi livelli si basano sui rapporti tra i numeri di Fibonacci e sono utilizzati per prevedere i movimenti dei prezzi.
• Informatica: La sequenza di Fibonacci è utilizzata in algoritmi di ricerca e ordinamento, nonché nella generazione di numeri casuali.
• Architettura e Design: Molti architetti e designer utilizzano il rapporto aureo per creare strutture e layout esteticamente gradevoli. Si ritiene che l'uso del rapporto aureo crei un senso di armonia ed equilibrio.
• Musica: Alcuni compositori hanno utilizzato i numeri di Fibonacci per strutturare le loro composizioni musicali, determinando la lunghezza delle sezioni, il numero di note in una melodia o il posizionamento degli accenti.

Questi sono solo alcuni esempi di come la sequenza di Fibonacci, nata da un problema di conigli, ha trovato applicazioni in campi sorprendentemente diversi.

Un Esempio Pratico: Il Trading Finanziario

Nel trading finanziario, i ritracciamenti di Fibonacci sono uno strumento popolare per identificare potenziali aree di supporto o resistenza. I trader utilizzano i rapporti di Fibonacci (23.6%, 38.2%, 50%, 61.8%, 100%) per proiettare potenziali livelli in cui il prezzo di un asset potrebbe invertire la sua direzione. Sebbene non siano infallibili, questi livelli possono fornire indicazioni preziose per prendere decisioni di trading.

Conclusione: Un'Eredità Duratura

La sequenza di Fibonacci, ideata da un brillante matematico pisano, continua ad affascinare e stupire. Dalle spirali dei girasoli alle strategie di trading finanziario, la sua presenza è innegabile. Che tu sia un appassionato di matematica, un amante della natura o semplicemente curioso del mondo che ti circonda, la sequenza di Fibonacci offre uno sguardo affascinante sulla bellezza e l'ordine nascosti nel caos apparente.

La prossima volta che osserverai un fiore o una conchiglia, prenditi un momento per apprezzare la magia dei numeri di Fibonacci e il genio di Leonardo Pisano, l'uomo che ha svelato uno dei segreti più affascinanti della natura.