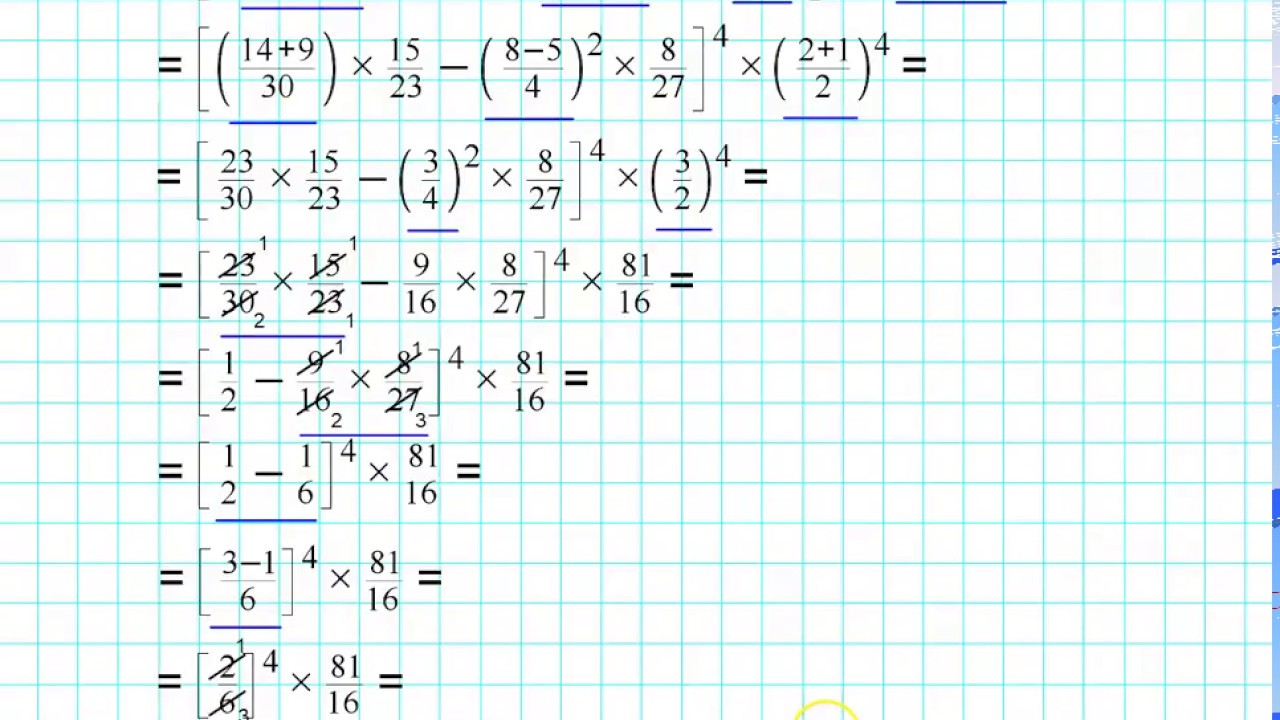
Espressioni Con Potenze Con Radice Quadrata

Chi non ha mai provato quella sensazione di smarrimento di fronte a un'espressione matematica che mescola potenze e radici quadrate? Quel momento in cui i simboli sembrano danzare in modo incomprensibile sulla pagina, e la frustrazione inizia a farsi sentire. Non siete soli. Molti studenti, dai primi approcci all'algebra fino ai corsi più avanzati, incontrano difficoltà nel districare questi nodi matematici. Ma non disperate! Con la giusta strategia e un po' di pratica, anche le espressioni più complesse diventano accessibili.

Comprendere i Concetti Fondamentali

Prima di tuffarci nella risoluzione di espressioni complesse, è fondamentale assicurarsi di aver compreso a fondo i concetti chiave. Come diceva Galileo Galilei: "Non si può insegnare niente a un uomo; lo si può solo aiutare a scoprirlo dentro di sé". Quindi, cerchiamo di "riscoprire" insieme le basi.

Potenze: Un Ripasso Veloce

Una potenza rappresenta una moltiplicazione ripetuta di un numero per se stesso. Ad esempio, 2³ (due elevato alla terza) significa 2 * 2 * 2 = 8. Il numero 2 è la base, mentre il numero 3 è l'esponente. Ricordiamoci alcune regole importanti:

a⁰ = 1 (qualunque numero diverso da zero elevato a zero è uguale a 1)
a¹ = a (qualunque numero elevato a 1 è uguale a se stesso)
a^-n = 1/aⁿ (un esponente negativo indica l'inverso della potenza)

Radici Quadrate: L'Operazione Inversa

La radice quadrata di un numero è quel numero che, moltiplicato per se stesso, dà il numero di partenza. Ad esempio, la radice quadrata di 9 (√9) è 3, perché 3 * 3 = 9. La radice quadrata può essere vista come l'operazione inversa dell'elevamento al quadrato.

√(a²) = |a| (la radice quadrata di un numero al quadrato è il valore assoluto del numero). Attenzione: la radice quadrata restituisce sempre un valore non negativo.

Espressioni con Potenze e Radici: Un Approccio Sistematico

Affrontare un'espressione che combina potenze e radici quadrate richiede un approccio metodico. Ecco una strategia passo-passo che può aiutarvi:

Semplificare le potenze all'interno della radice: Se possibile, calcola prima le potenze che si trovano all'interno della radice. Ad esempio, in √(2⁴), calcola prima 2⁴ = 16.
Riscrivere le radici come potenze frazionarie: Questa è una tecnica chiave. Ricorda che la radice quadrata di un numero (√a) è equivalente a a^1/2. Questa trasformazione permette di applicare le proprietà delle potenze in modo più agevole. La radice cubica sarebbe a^1/3, la radice quarta a^1/4 e così via.
Applicare le proprietà delle potenze: Una volta che le radici sono state trasformate in potenze frazionarie, puoi utilizzare le proprietà delle potenze per semplificare l'espressione. Ricorda le proprietà:
- Prodotto di potenze con la stessa base: a^m * aⁿ = a^m+n
- Quoziente di potenze con la stessa base: a^m / aⁿ = a^m-n
- Potenza di una potenza: (a^m)ⁿ = a^m*n
Semplificare ulteriormente: Dopo aver applicato le proprietà delle potenze, cerca di semplificare ulteriormente l'espressione, combinando termini simili e riducendo le frazioni.
Calcolare il risultato finale: Infine, calcola il valore numerico dell'espressione semplificata.

Esempi Pratici

Vediamo alcuni esempi concreti per illustrare l'approccio sistematico.

Esempio 1: √(4³)

Calcola la potenza all'interno della radice: 4³ = 64
Quindi, √(64) = 8

Esempio 2: (√9)²

Calcola la radice quadrata: √9 = 3
Eleva il risultato al quadrato: 3² = 9

Esempio 3: √(x⁴ * y²)

Riscrivi come potenze: (x⁴ * y²)^1/2
Applica la potenza ad ogni termine: x^4*(1/2) * y^2*(1/2) = x² * y

Esempio 4: (√(a))⁶

Riscrivi la radice come potenza frazionaria: (a^1/2)⁶
Applica la proprietà della potenza di una potenza: a^(1/2)*6 = a³

Strumenti Utili per l'Apprendimento

Oltre alla pratica costante, esistono diversi strumenti che possono facilitare l'apprendimento delle espressioni con potenze e radici quadrate:

Calcolatrici scientifiche: Molte calcolatrici scientifiche sono in grado di semplificare espressioni con potenze e radici, permettendoti di verificare i tuoi risultati e di esplorare diversi scenari.
Software di algebra computazionale (CAS): Software come Wolfram Alpha o GeoGebra possono manipolare espressioni algebriche, fornire soluzioni passo-passo e visualizzare grafici.
Risorse online: Esistono numerosi siti web e canali YouTube che offrono tutorial, esercizi e spiegazioni dettagliate sulle potenze e le radici quadrate. Cercate risorse create da insegnanti di matematica qualificati.
Libri di testo ed eserciziari: Un buon libro di testo o un eserciziario ben strutturato può fornire una solida base teorica e una vasta gamma di esercizi di difficoltà crescente.

Errori Comuni da Evitare

Durante la risoluzione di espressioni con potenze e radici quadrate, è importante evitare alcuni errori comuni:

Confondere l'ordine delle operazioni: Ricorda di seguire sempre l'ordine delle operazioni (parentesi, esponenti, moltiplicazioni e divisioni, addizioni e sottrazioni - PEMDAS o BODMAS).
Applicare le proprietà delle potenze in modo errato: Assicurati di comprendere a fondo le proprietà delle potenze e di applicarle correttamente. Ad esempio, non puoi sommare potenze con la stessa base se non sono moltiplicate tra loro.
Dimenticare il valore assoluto: Quando semplifichi la radice quadrata di un quadrato (√(a²)), ricorda che il risultato è il valore assoluto di a (|a|).
Non semplificare al massimo: Cerca sempre di semplificare l'espressione al massimo, combinando termini simili e riducendo le frazioni.

L'Importanza della Pratica

Come per ogni disciplina, la pratica è fondamentale per acquisire padronanza delle espressioni con potenze e radici quadrate. "La pratica rende perfetti," dice il proverbio. Risolvi un'ampia varietà di esercizi, partendo da quelli più semplici e gradualmente aumentando la difficoltà. Non aver paura di commettere errori; gli errori sono un'opportunità di apprendimento. Analizza i tuoi errori e cerca di capire perché hai sbagliato. Chiedi aiuto al tuo insegnante o a un compagno di classe se hai difficoltà.

Conclusione

Affrontare le espressioni con potenze e radici quadrate può sembrare scoraggiante all'inizio, ma con una solida comprensione dei concetti fondamentali, un approccio sistematico e tanta pratica, puoi superare le difficoltà e acquisire sicurezza nelle tue capacità matematiche. Ricorda, la matematica è un linguaggio, e come ogni lingua, richiede tempo e dedizione per essere padroneggiata. Non arrenderti, continua a esercitarti e presto ti troverai a risolvere espressioni complesse con facilità e sicurezza.