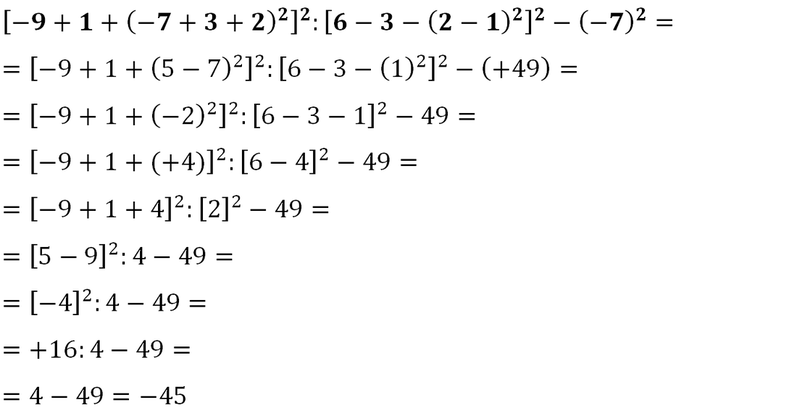Espressioni Con Numeri Relativi E Potenze

Quante volte ci siamo trovati di fronte a un'espressione matematica, magari con numeri relativi e potenze, e abbiamo sentito un brivido di incertezza? Non siete soli. Molti studenti, genitori che cercano di aiutare i figli con i compiti, e persino alcuni insegnanti, a volte si sentono sopraffatti da questo argomento. La matematica, si sa, può sembrare un labirinto, ma con la giusta guida e un approccio strutturato, anche le espressioni più complesse possono essere affrontate con successo.

L'obiettivo di questo articolo è proprio quello di demistificare le espressioni con numeri relativi e potenze, fornendo spiegazioni chiare, esempi pratici e consigli utili per superare le difficoltà più comuni. Affronteremo l'argomento passo dopo passo, partendo dalle basi e arrivando a concetti più avanzati, il tutto in un linguaggio accessibile e senza inutili tecnicismi.

Cosa sono i Numeri Relativi?

Partiamo dalle fondamenta: i numeri relativi. Questi numeri non sono altro che i numeri che conosciamo (1, 2, 3, ecc.), arricchiti di un segno, + (positivo) o - (negativo). I numeri positivi indicano una quantità sopra lo zero, mentre i numeri negativi indicano una quantità sotto lo zero. Pensate alla temperatura: +10°C è sopra lo zero, mentre -5°C è sotto lo zero. Lo 0 è un numero relativo, ma non è né positivo né negativo.

Perché sono importanti? Perché ci permettono di rappresentare situazioni che i numeri naturali (1, 2, 3...) non possono descrivere. Pensate a un debito (un numero negativo) o a un'altezza sotto il livello del mare.

Operazioni con i Numeri Relativi:

Addizione e Sottrazione

L'addizione e la sottrazione tra numeri relativi richiedono attenzione ai segni. Ecco le regole fondamentali:

• Somma di numeri con lo stesso segno: Si sommano i valori assoluti e si mantiene il segno.
  • Esempio: (+3) + (+5) = +8
  • Esempio: (-2) + (-4) = -6
• Somma di numeri con segno diverso: Si sottrae il valore assoluto minore dal valore assoluto maggiore e si prende il segno del numero con valore assoluto maggiore.
  • Esempio: (+7) + (-3) = +4 (7-3 = 4, e 7 è maggiore con segno positivo)
  • Esempio: (-9) + (+2) = -7 (9-2 = 7, e 9 è maggiore con segno negativo)
• Sottrazione: Per sottrarre un numero relativo, si somma il suo opposto. L'opposto di un numero è lo stesso numero con il segno cambiato.
  • Esempio: (+5) - (+2) = (+5) + (-2) = +3
  • Esempio: (-3) - (-1) = (-3) + (+1) = -2

Moltiplicazione e Divisione

Anche per la moltiplicazione e la divisione, il segno è fondamentale. La regola è semplice:

• Segni uguali: Il risultato è positivo. (+ * + = +; - * - = +; + / + = +; - / - = +)
• Segni diversi: Il risultato è negativo. (+ * - = -; - * + = -; + / - = -; - / + = -)

Esempi:

• (+4) * (+2) = +8
• (-3) * (-5) = +15
• (+6) * (-1) = -6
• (-8) / (+2) = -4

Cosa sono le Potenze?

Una potenza è un modo abbreviato per scrivere una moltiplicazione ripetuta di un numero per se stesso. Il numero che viene moltiplicato si chiama base, e il numero che indica quante volte la base deve essere moltiplicata si chiama esponente.

Ad esempio, 2³ (due elevato alla terza) significa 2 * 2 * 2 = 8. Qui, 2 è la base e 3 è l'esponente.

Regole delle Potenze:

• Qualsiasi numero (diverso da zero) elevato a 0 è uguale a 1: a⁰ = 1 (es: 5⁰ = 1)
• Qualsiasi numero elevato a 1 è uguale a se stesso: a¹ = a (es: 7¹ = 7)
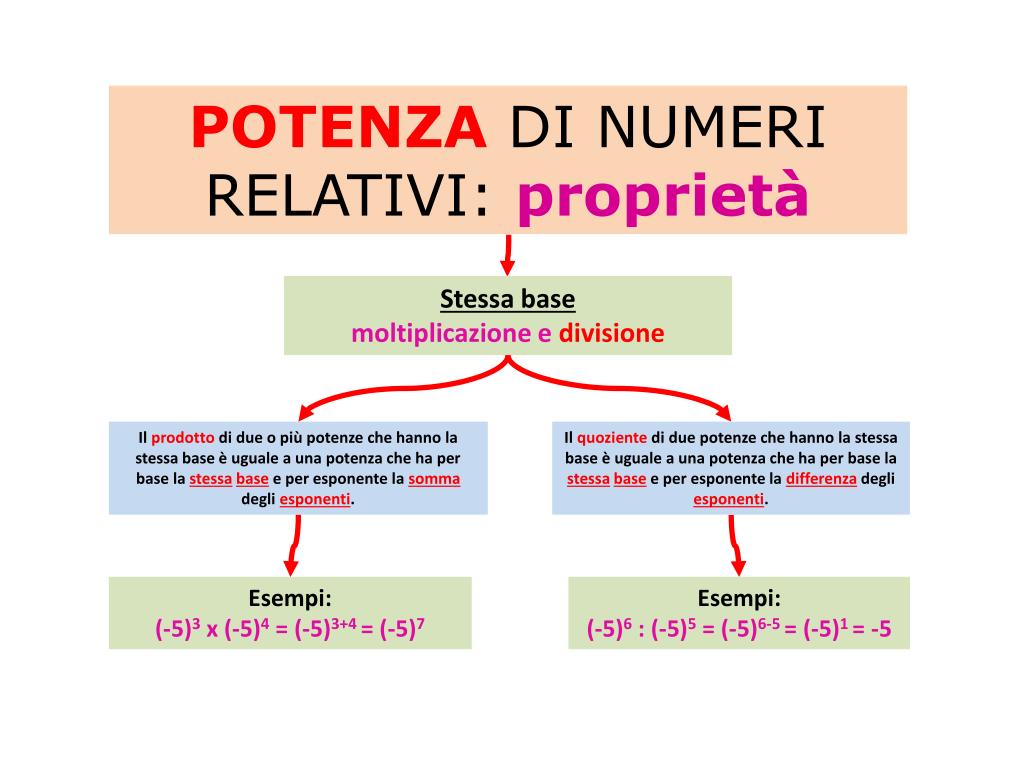
• Prodotto di potenze con la stessa base: Si sommano gli esponenti: a^m * aⁿ = a^m+n (es: 2² * 2³ = 2⁵ = 32)
• Quoziente di potenze con la stessa base: Si sottraggono gli esponenti: a^m / aⁿ = a^m-n (es: 3⁵ / 3² = 3³ = 27)
• Potenza di una potenza: Si moltiplicano gli esponenti: (a^m)ⁿ = a^m*n (es: (2²)³ = 2⁶ = 64)

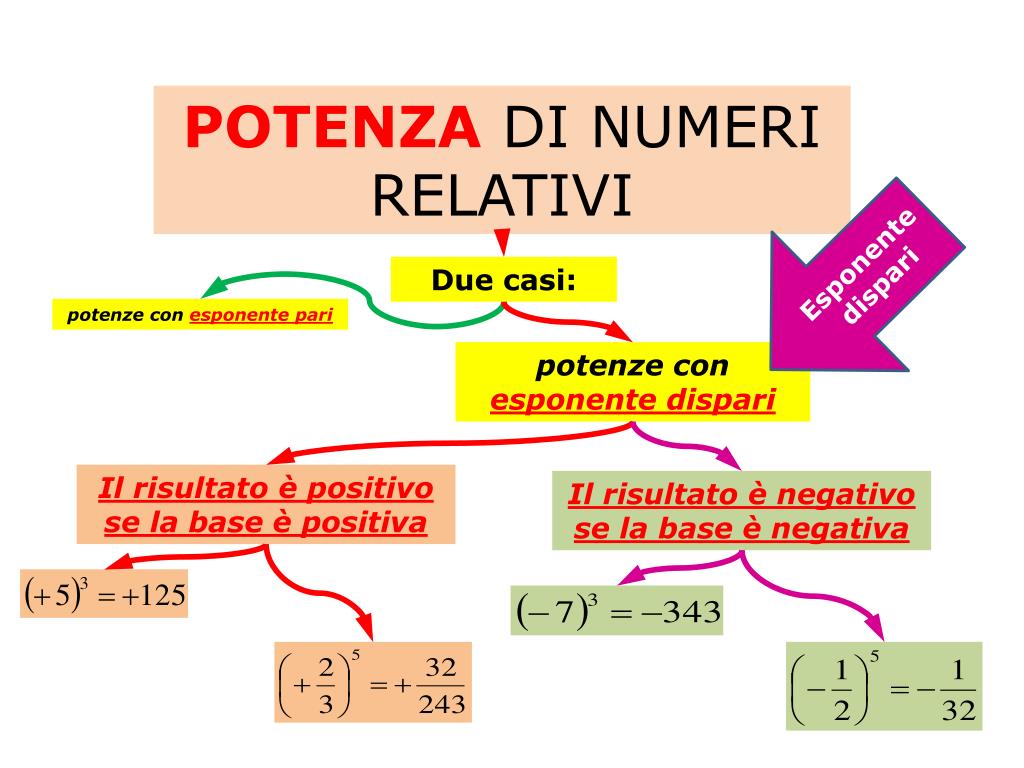
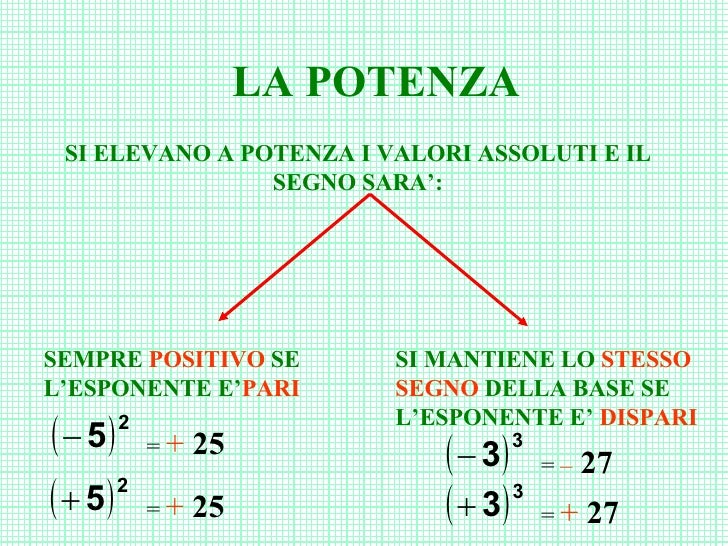
Potenze con Base Negativa

Quando la base di una potenza è negativa, il segno del risultato dipende dall'esponente:

• Esponente pari: Il risultato è positivo. (-a)ⁿ = + (se n è pari) (es: (-2)² = +4)
• Esponente dispari: Il risultato è negativo. (-a)ⁿ = - (se n è dispari) (es: (-2)³ = -8)

Espressioni con Numeri Relativi e Potenze: L'Ordine delle Operazioni

Ora che abbiamo rivisto i numeri relativi e le potenze, possiamo affrontare le espressioni che li contengono. La chiave per risolvere correttamente un'espressione è seguire l'ordine delle operazioni, spesso ricordato con l'acronimo PEMDAS (o BODMAS in alcuni paesi di lingua inglese):

1. Parentesi (o Brackets): Si risolvono prima le operazioni all'interno delle parentesi (tonde, quadre e graffe), partendo dalle più interne.
2. Esponenti (o Orders): Si calcolano le potenze.
3. Moltiplicazioni e Divisioni: Si eseguono moltiplicazioni e divisioni nell'ordine in cui compaiono, da sinistra a destra.
4. Addizioni e Sottrazioni: Si eseguono addizioni e sottrazioni nell'ordine in cui compaiono, da sinistra a destra.

Esempio Pratico:

Consideriamo l'espressione: 2 * (-3)² + 5 - (10 / -2)

1. Parentesi: (10 / -2) = -5
2. Esponenti: (-3)² = +9
3. Moltiplicazioni: 2 * (+9) = +18
4. Sostituzione: +18 + 5 - (-5)
5. Sottrazione (trasformata in addizione): +18 + 5 + 5
6. Addizioni: +18 + 5 + 5 = +28

Quindi, il risultato dell'espressione è +28.

Consigli Pratici e Trucchi

• Scrivere tutti i passaggi: Non cercare di fare tutto a mente. Scrivere ogni passaggio aiuta a evitare errori e a tenere traccia del ragionamento.
• Fare attenzione ai segni: Gli errori più comuni derivano da errori con i segni. Controllare attentamente ogni operazione.
• Usare le parentesi: Le parentesi possono essere utili per chiarire l'ordine delle operazioni, soprattutto quando si ha a che fare con espressioni complesse.
• Verificare il risultato: Se possibile, verificare il risultato utilizzando una calcolatrice scientifica o un'applicazione online.
• Praticare, praticare, praticare: La matematica, come qualsiasi altra disciplina, richiede pratica. Risolvere molti esercizi aiuta a consolidare le conoscenze e a sviluppare la sicurezza.

Esempio di Esercizio per la Casa:

Chiedete ai vostri figli di risolvere la seguente espressione, guidandoli passo dopo passo:

5 - (-2)³ * 3 + (12 / -4) - 1

Soluzione (non mostratela subito!):

1. (-2)³ = -8
2. (12 / -4) = -3
3. 5 - (-8) * 3 + (-3) - 1
4. 5 - (-24) + (-3) - 1
5. 5 + 24 - 3 - 1
6. 29 - 3 - 1
7. 26 - 1
8. 25

Il risultato è 25.

Conclusione

Le espressioni con numeri relativi e potenze possono sembrare complesse, ma con una buona comprensione dei concetti di base, un approccio strutturato e molta pratica, possono essere affrontate con successo. Ricordate l'importanza dell'ordine delle operazioni (PEMDAS), prestate attenzione ai segni e non abbiate paura di chiedere aiuto quando necessario. La matematica è un linguaggio che, una volta decifrato, può aprire le porte a un mondo di possibilità.

Non scoraggiatevi di fronte alle difficoltà. Ogni errore è un'opportunità per imparare e migliorare. Con perseveranza e un po' di impegno, potrete superare qualsiasi ostacolo e padroneggiare l'arte delle espressioni matematiche.