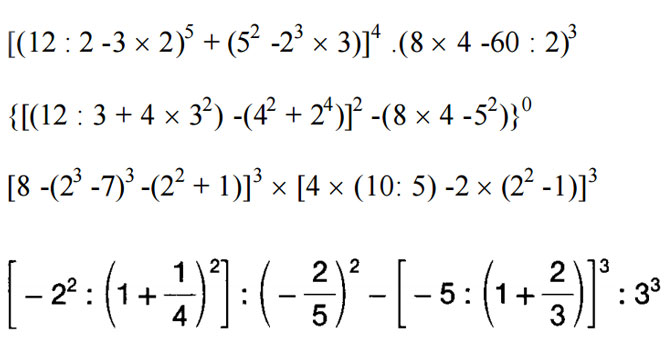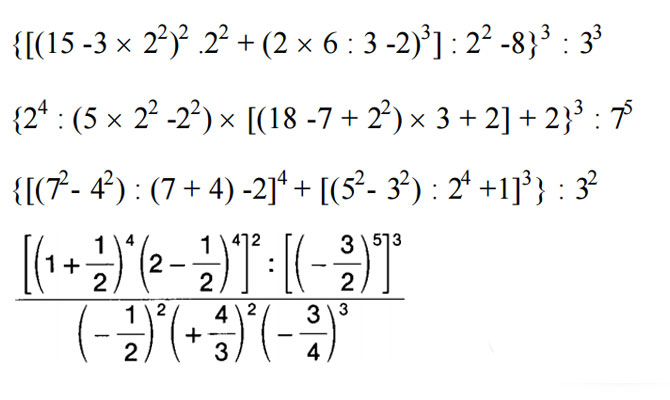Esercizi Sulle Espressioni Con Le Potenze

Le espressioni con le potenze rappresentano un elemento fondamentale dell'algebra e dell'aritmetica. Comprendere come risolverle correttamente è cruciale per affrontare concetti matematici più avanzati, dalla fisica all'ingegneria. Questo articolo esplorerà nel dettaglio come affrontare gli esercizi sulle espressioni con le potenze, fornendo spiegazioni chiare, esempi pratici e consigli utili per evitare errori comuni.

Le Basi delle Potenze

Prima di affrontare esercizi complessi, è essenziale comprendere le basi delle potenze. Una potenza è un modo conciso per rappresentare la moltiplicazione ripetuta di un numero per se stesso. Si esprime nella forma aⁿ, dove a è la base e n è l'esponente. La base è il numero che viene moltiplicato, e l'esponente indica quante volte la base viene moltiplicata per se stessa.

Ad esempio, 2³ significa 2 moltiplicato per se stesso tre volte: 2 * 2 * 2 = 8. Quindi, 2³ = 8.

Proprietà Fondamentali delle Potenze

Esistono diverse proprietà fondamentali che regolano le operazioni con le potenze. La conoscenza di queste proprietà è indispensabile per semplificare le espressioni e risolverle correttamente. Eccone alcune:

Prodotto di potenze con la stessa base: a^m * aⁿ = a^m+n. Quando si moltiplicano potenze con la stessa base, si sommano gli esponenti. Esempio: 2² * 2³ = 2²⁺³ = 2⁵ = 32.
Quoziente di potenze con la stessa base: a^m / aⁿ = a^m-n. Quando si dividono potenze con la stessa base, si sottraggono gli esponenti. Esempio: 3⁵ / 3² = 3^5-2 = 3³ = 27.
Potenza di una potenza: (a^m)ⁿ = a^m*n. Quando si eleva una potenza a un'altra potenza, si moltiplicano gli esponenti. Esempio: (2³)² = 2^3*2 = 2⁶ = 64.
Potenza di un prodotto: (a * b)ⁿ = aⁿ * bⁿ. La potenza di un prodotto è uguale al prodotto delle potenze. Esempio: (2 * 3)² = 2² * 3² = 4 * 9 = 36.
Potenza di un quoziente: (a / b)ⁿ = aⁿ / bⁿ. La potenza di un quoziente è uguale al quoziente delle potenze. Esempio: (6 / 2)² = 6² / 2² = 36 / 4 = 9.
Potenza con esponente zero: a⁰ = 1 (con a ≠ 0). Qualsiasi numero (diverso da zero) elevato a 0 è uguale a 1. Esempio: 5⁰ = 1.
Potenza con esponente negativo: a^-n = 1 / aⁿ. Una potenza con esponente negativo è uguale all'inverso della potenza con l'esponente positivo. Esempio: 2^-3 = 1 / 2³ = 1 / 8.

Esercizi Sulle Espressioni Con Le Potenze: Esempi Pratici

Ora che abbiamo ripassato le proprietà fondamentali, vediamo alcuni esempi pratici di esercizi sulle espressioni con le potenze.

Esempio 1: Semplificazione di un'espressione

Consideriamo l'espressione: (3² * 3⁴) / 3³.

Applichiamo prima la proprietà del prodotto di potenze con la stessa base al numeratore: 3² * 3⁴ = 3²⁺⁴ = 3⁶.

Ora abbiamo: 3⁶ / 3³. Applichiamo la proprietà del quoziente di potenze con la stessa base: 3⁶ / 3³ = 3^6-3 = 3³.

Quindi, il risultato finale è 3³ = 27.

Esempio 2: Espressioni con esponenti negativi

Consideriamo l'espressione: 2^-2 + 4^-1.

Applichiamo la proprietà degli esponenti negativi: 2^-2 = 1 / 2² = 1 / 4 e 4^-1 = 1 / 4¹ = 1 / 4.

Ora abbiamo: 1 / 4 + 1 / 4 = 2 / 4 = 1 / 2.

Quindi, il risultato finale è 1 / 2.

Esempio 3: Espressioni con potenza di una potenza

Consideriamo l'espressione: (5²)³ * 5^-1.

Applichiamo la proprietà della potenza di una potenza: (5²)³ = 5^2*3 = 5⁶.

Ora abbiamo: 5⁶ * 5^-1. Applichiamo la proprietà del prodotto di potenze con la stessa base: 5⁶ * 5^-1 = 5^6+(-1) = 5⁵.

Quindi, il risultato finale è 5⁵ = 3125.

Esempio 4: Combinazione di proprietà

Consideriamo l'espressione: [(2³ * 2^-1) / 2²]².

Innanzitutto, semplifichiamo l'interno delle parentesi quadre. Applichiamo la proprietà del prodotto di potenze con la stessa base: 2³ * 2^-1 = 2^3+(-1) = 2².

Ora abbiamo: [2² / 2²]². Applichiamo la proprietà del quoziente di potenze con la stessa base: 2² / 2² = 2^2-2 = 2⁰ = 1.

Infine, abbiamo: 1² = 1.

Quindi, il risultato finale è 1.

Errori Comuni da Evitare

Quando si risolvono esercizi sulle espressioni con le potenze, è fondamentale evitare alcuni errori comuni:

Confondere l'esponente con la moltiplicazione: aⁿ non significa a * n, ma a moltiplicato per se stesso n volte.
Ignorare l'ordine delle operazioni: Ricordarsi sempre di seguire l'ordine delle operazioni (parentesi, esponenti, moltiplicazioni e divisioni, addizioni e sottrazioni - PEMDAS o BODMAS).
Applicare le proprietà in modo errato: Assicurarsi di applicare correttamente le proprietà delle potenze, soprattutto quando si tratta di esponenti negativi o frazionari.
Dimenticare le regole del segno: Prestare attenzione ai segni quando si lavora con numeri negativi. (-2)² = 4 mentre -2² = -4.
Non semplificare completamente: Assicurarsi di semplificare l'espressione fino alla sua forma più semplice.

Applicazioni Reali delle Potenze

Le potenze non sono solo un concetto astratto; hanno numerose applicazioni nel mondo reale:

Informatica: La capacità di calcolo dei computer è espressa in termini di potenze di 2 (bit, byte, kilobyte, megabyte, gigabyte, ecc.).
Scienza: La notazione scientifica, che utilizza le potenze di 10, è fondamentale per esprimere numeri molto grandi o molto piccoli, come la distanza tra le stelle o le dimensioni di un atomo.
Finanza: L'interesse composto, che cresce esponenzialmente nel tempo, si basa sul concetto di potenza.
Fisica: Molte leggi fisiche, come la legge di gravitazione universale di Newton, coinvolgono potenze.
Ingegneria: Le potenze sono utilizzate nel calcolo di aree, volumi e momenti di inerzia.

Ad esempio, la velocità della luce è approssimativamente 3 x 10⁸ metri al secondo. Questo utilizzo della potenza di 10 rende molto più gestibile un numero altrimenti molto grande.

Conclusione e Call to Action

La padronanza degli esercizi sulle espressioni con le potenze è una competenza essenziale per chiunque studi matematica o scienze. Comprendere le proprietà fondamentali, evitare gli errori comuni e fare pratica con esercizi di diversa difficoltà sono i passi chiave per raggiungere questo obiettivo.

Ti invito a esercitarti regolarmente con espressioni di difficoltà crescente. Cerca esercizi online, consulta libri di testo e non esitare a chiedere aiuto se incontri difficoltà. Ricorda che la pratica rende perfetti! Buon lavoro!