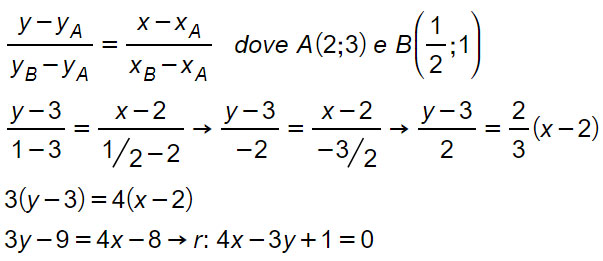Distanza Di Un Punto Da Una Retta

Avete mai avuto la necessità di calcolare la distanza esatta tra un punto specifico e una linea retta? Magari per un problema di geometria, per sviluppare un'applicazione di grafica, o semplicemente per curiosità? Questo articolo è pensato per voi! Sia che siate studenti alle prese con la matematica, appassionati di programmazione, o semplicemente persone curiose, vi guideremo passo dopo passo attraverso il concetto di distanza di un punto da una retta, fornendovi gli strumenti necessari per calcolarla in modo semplice e comprensibile.

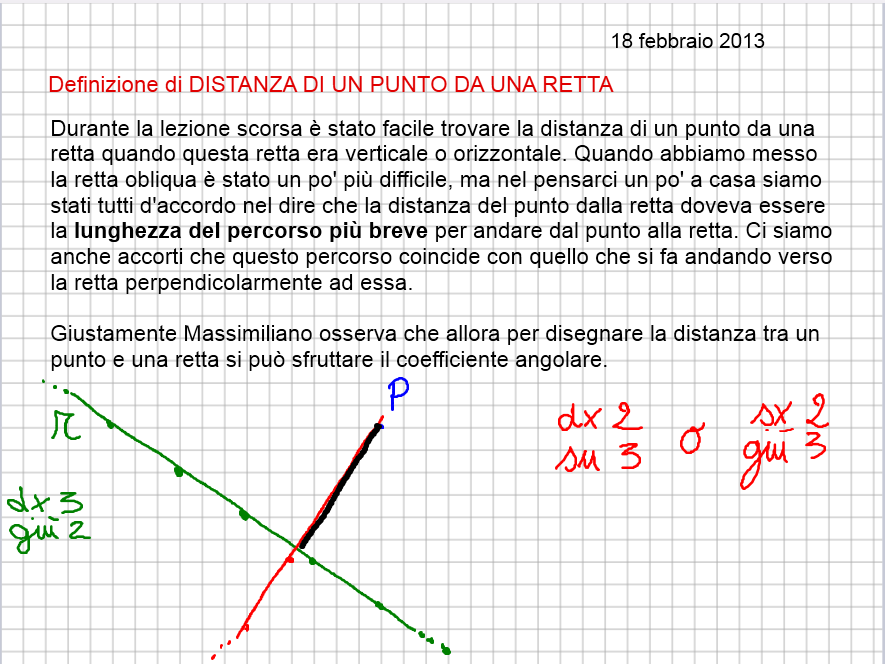
Cos'è la Distanza di un Punto da una Retta?

La distanza di un punto da una retta è definita come la lunghezza del segmento perpendicolare che congiunge il punto alla retta. Immaginate di avere un punto sospeso sopra una linea: la distanza è la lunghezza del filo più corto che potete tirare dal punto alla linea, assicurandovi che il filo sia perfettamente verticale (perpendicolare).

In termini matematici, si tratta della minima distanza tra il punto e qualsiasi punto sulla retta. Qualsiasi altro segmento che collega il punto alla retta, ma che non sia perpendicolare, sarà più lungo.

Perché è Importante?

Il concetto di distanza di un punto da una retta ha numerose applicazioni in diversi campi:

Geometria Analitica: Fondamentale per risolvere problemi geometrici e per definire figure e relazioni nello spazio.
Grafica Computazionale: Utilizzata per il rendering di immagini 2D e 3D, per calcolare collisioni e per determinare la posizione di oggetti rispetto a linee e piani.
Fisica: Utile per calcolare distanze e percorsi ottimali, ad esempio, la traiettoria di un raggio di luce che si riflette su una superficie.
Ingegneria: Utilizzata nella progettazione di strutture, nella navigazione e in molti altri ambiti.
Machine Learning: Alcuni algoritmi utilizzano la distanza di un punto da un iperpiano per classificare i dati (Support Vector Machines).

Come Calcolare la Distanza: La Formula Fondamentale

La formula per calcolare la distanza di un punto da una retta è relativamente semplice, ma è importante comprenderne l'origine. Consideriamo un punto P di coordinate (x₀, y₀) e una retta r definita dall'equazione implicita:

Ax + By + C = 0

La distanza, che indicheremo con d(P, r), è data da:

d(P, r) = |Ax₀ + By₀ + C| / √(A² + B²)

Analizziamo gli elementi della formula:

A, B, C: Sono i coefficienti dell'equazione implicita della retta.
x₀, y₀: Sono le coordinate del punto P.
|...|: Indica il valore assoluto, garantendo che la distanza sia sempre un numero positivo.
√(A² + B²): Rappresenta la norma del vettore normale alla retta (A, B).

Spiegazione Dettagliata della Formula

La formula deriva dalla proiezione del vettore che congiunge un punto qualsiasi sulla retta al punto P sul vettore normale alla retta. In altre parole, stiamo calcolando la lunghezza della componente del vettore che è perpendicolare alla retta. Il valore assoluto assicura che la distanza sia sempre positiva, indipendentemente dalla posizione del punto rispetto alla retta.

Esempio Pratico

Calcoliamo la distanza del punto P(2, 3) dalla retta r: 3x + 4y - 5 = 0.

Identifichiamo i coefficienti: A = 3, B = 4, C = -5.
Sostituiamo nella formula: d(P, r) = |(3 * 2) + (4 * 3) - 5| / √(3² + 4²) d(P, r) = |6 + 12 - 5| / √(9 + 16) d(P, r) = |13| / √25 d(P, r) = 13 / 5
Risultato: La distanza del punto P(2, 3) dalla retta r è 13/5 = 2.6.

Passaggi Chiave per Calcolare la Distanza

Identificare il Punto: Assicurarsi di avere le coordinate (x₀, y₀) del punto P.
Ottenere l'Equazione della Retta: La retta deve essere espressa in forma implicita: Ax + By + C = 0. Se la retta è data in un'altra forma (es. y = mx + q), è necessario trasformarla nella forma implicita.
Sostituire nella Formula: Inserire i valori di A, B, C, x₀ e y₀ nella formula.
Calcolare il Valore Assoluto: Assicurarsi di prendere il valore assoluto del numeratore.
Calcolare la Radice Quadrata: Calcolare la radice quadrata del denominatore.
Dividere: Dividere il valore assoluto del numeratore per la radice quadrata del denominatore.
Il Risultato: Il risultato ottenuto è la distanza del punto dalla retta.

Come Trasformare l'Equazione della Retta in Forma Implicita

Se l'equazione della retta è data in forma esplicita (y = mx + q), è necessario trasformarla in forma implicita (Ax + By + C = 0). Questo si fa semplicemente portando tutti i termini da un lato dell'equazione:

y = mx + q => mx - y + q = 0

Quindi, in questo caso, A = m, B = -1 e C = q.

Esercizi Proposti

Mettete alla prova le vostre conoscenze risolvendo questi esercizi:

Calcolare la distanza del punto (1, -2) dalla retta x + 2y - 3 = 0.
Calcolare la distanza del punto (0, 0) dalla retta 5x - 12y + 13 = 0.
Calcolare la distanza del punto (-3, 4) dalla retta y = 2x + 1. (Ricorda di trasformare l'equazione in forma implicita!)

Approfondimenti e Variazioni

Distanza di un Punto da un Segmento

Se si vuole calcolare la distanza di un punto da un segmento di retta, il procedimento è leggermente più complesso. Innanzitutto, si calcola la distanza del punto dalla retta che contiene il segmento. Se il punto di proiezione del punto sulla retta (il punto sulla retta più vicino al punto dato) cade all'interno del segmento, allora la distanza calcolata è la distanza del punto dal segmento. Se, invece, il punto di proiezione cade al di fuori del segmento, allora la distanza del punto dal segmento è la distanza del punto da uno degli estremi del segmento (quello più vicino).

Generalizzazioni in Spazi a Dimensioni Superiori

Il concetto di distanza di un punto da una retta può essere generalizzato a spazi a dimensioni superiori. Ad esempio, in uno spazio tridimensionale, si può calcolare la distanza di un punto da un piano. La formula è simile a quella per la distanza di un punto da una retta, ma con un termine aggiuntivo per la terza coordinata.

Strumenti Online per il Calcolo della Distanza

Esistono numerosi strumenti online che permettono di calcolare la distanza di un punto da una retta in modo rapido e semplice. Basta inserire le coordinate del punto e l'equazione della retta, e lo strumento fornirà il risultato. Questi strumenti possono essere utili per verificare i propri calcoli o per risolvere problemi velocemente.

Conclusione

Speriamo che questa guida vi abbia fornito una comprensione chiara e completa del concetto di distanza di un punto da una retta. Che siate studenti, professionisti o semplicemente curiosi, ora avete gli strumenti per calcolare questa distanza in modo preciso e sicuro. Ricordate, la matematica è uno strumento potente che ci aiuta a comprendere e a navigare il mondo che ci circonda. Continuate a esplorare, a sperimentare e a porvi domande: la conoscenza è un viaggio senza fine!

La capacità di calcolare la distanza di un punto da una retta non è solo un esercizio matematico, ma uno strumento versatile che può essere applicato in una vasta gamma di contesti reali. Utilizzate questa conoscenza per risolvere problemi, per creare soluzioni innovative e per migliorare la vostra comprensione del mondo.