Determina Il Dominio Delle Seguenti Funzioni

Ciao a tutti! Immaginate di trovarvi all'inizio di un viaggio. Un viaggio attraverso il meraviglioso mondo della matematica, un viaggio che, passo dopo passo, vi svelerà segreti inaspettati e vi farà sentire più forti e sicuri di voi stessi. Oggi, il nostro punto di partenza è un concetto fondamentale: Il Dominio delle Funzioni.

Ci approcceremo a questo argomento come faremmo con un nuovo amico: con curiosità, pazienza e rispetto. Invece di vederlo come un ostacolo, cerchiamo di considerarlo come un'opportunità per affinare la nostra capacità di osservazione e di ragionamento.

Esplorando il Terreno di Gioco

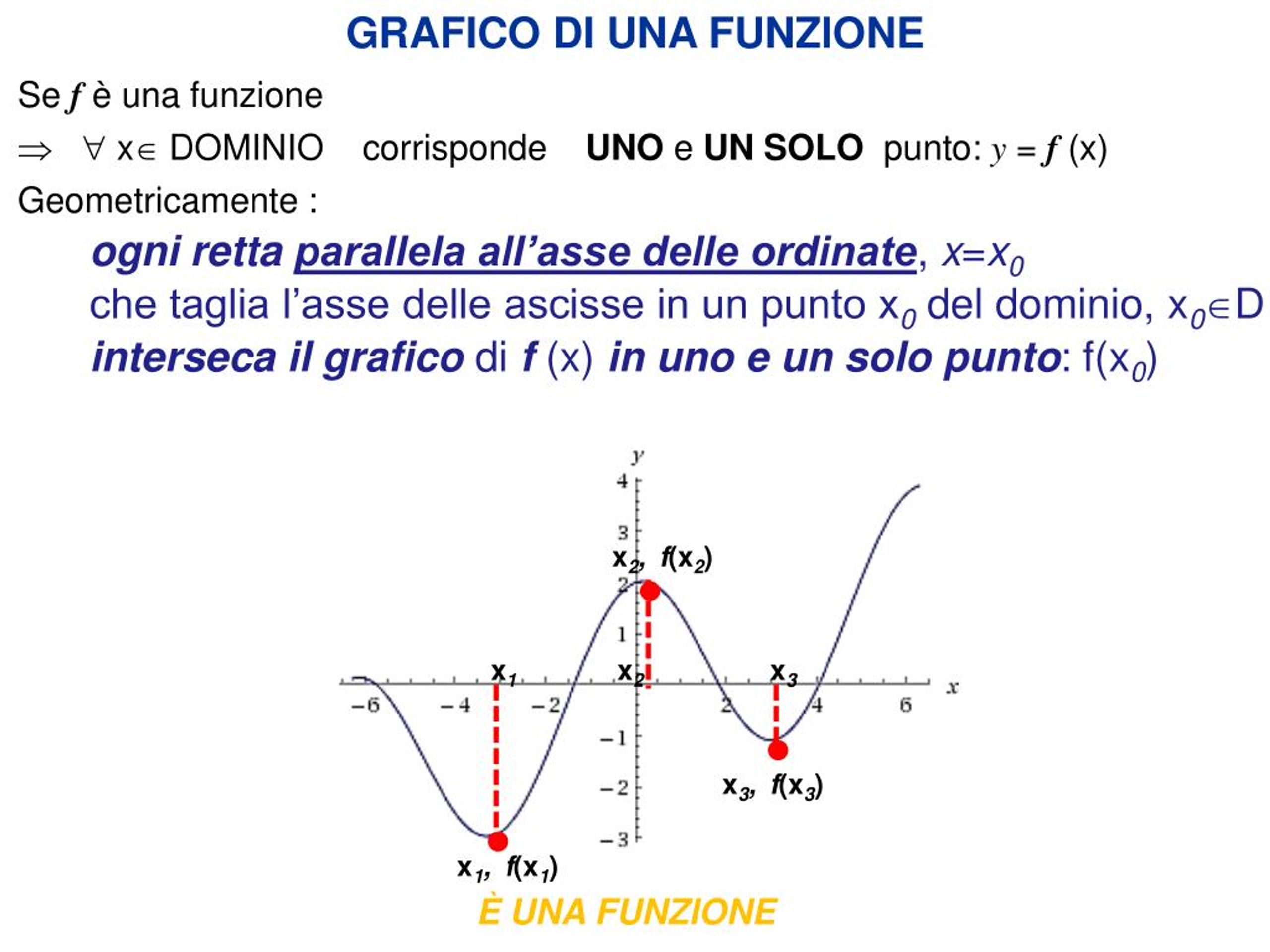
Considerate una funzione come una macchina che trasforma un ingrediente (un numero, la nostra x) in un prodotto finito (un altro numero, la nostra y). Il dominio di questa funzione è semplicemente l'insieme di tutti gli ingredienti validi che possiamo "dare in pasto" alla macchina senza romperla. In altre parole, sono tutti i valori di x per i quali la funzione ha un senso e produce un risultato reale.

Esercitiamoci Insieme

Adesso, mettiamoci alla prova con qualche esempio. Immaginate che vi venga chiesto di determinare il dominio delle seguenti funzioni:

1) f(x) = 3x + 5

Questa è una funzione lineare. Possiamo inserire qualsiasi numero al posto di x? Certo che sì! Non ci sono divisioni per zero, radici quadrate di numeri negativi o logaritmi di zero. Quindi, il dominio di questa funzione è l'insieme di tutti i numeri reali, che possiamo scrivere come (-∞, +∞).

2) g(x) = 1 / (x - 2)

Qui la situazione è diversa. Abbiamo una divisione. Sappiamo che non possiamo dividere per zero. Quindi, dobbiamo escludere tutti i valori di x che renderebbero il denominatore (x - 2) uguale a zero. Questo accade quando x = 2. Pertanto, il dominio di questa funzione è l'insieme di tutti i numeri reali eccetto 2, che possiamo scrivere come (-∞, 2) U (2, +∞).

3) h(x) = √ (x + 4)

In questo caso, abbiamo una radice quadrata. Ricordiamo che non possiamo calcolare la radice quadrata di un numero negativo (almeno, non nei numeri reali). Quindi, dobbiamo assicurarci che l'espressione sotto la radice, (x + 4), sia maggiore o uguale a zero. Questo significa che x + 4 ≥ 0, il che implica x ≥ -4. Quindi, il dominio di questa funzione è l'insieme di tutti i numeri reali maggiori o uguali a -4, che possiamo scrivere come [-4, +∞).

4) k(x) = log(x)

Consideriamo ora il logaritmo. Il logaritmo di un numero negativo o di zero non è definito. Pertanto, dobbiamo richiedere che x sia strettamente maggiore di zero (x > 0). Il dominio di questa funzione è quindi l'insieme di tutti i numeri reali positivi, che possiamo scrivere come (0, +∞).

Ogni funzione ci pone una piccola sfida, un piccolo enigma da risolvere. E la bellezza sta proprio in questo: nel processo di scoperta, nel ragionamento logico, nella soddisfazione di aver compreso qualcosa di nuovo.

Imparare con Umiltà e Perseveranza

Non scoraggiatevi se all'inizio incontrate delle difficoltà. La matematica, come qualsiasi altra disciplina, richiede pratica e dedizione. Siate umili, riconoscete i vostri errori e imparate da essi. Chiedete aiuto quando ne avete bisogno, collaborare con i vostri compagni e non abbiate paura di sperimentare.

Ricordate che ogni problema risolto è una vittoria, un passo avanti verso la vostra crescita personale e intellettuale. Il dominio delle funzioni non è solo un concetto matematico, ma una metafora della vita stessa. Impariamo a riconoscere i limiti, ad accettare le restrizioni e a trovare la libertà all'interno di esse.

Spero che questo piccolo viaggio vi sia piaciuto e vi abbia ispirato a esplorare ulteriormente il meraviglioso mondo della matematica. Siate curiosi, siate perseveranti e non smettete mai di imparare! Ricordate Galileo Galilei: “La matematica è l'alfabeto con cui Dio ha scritto l'universo”.