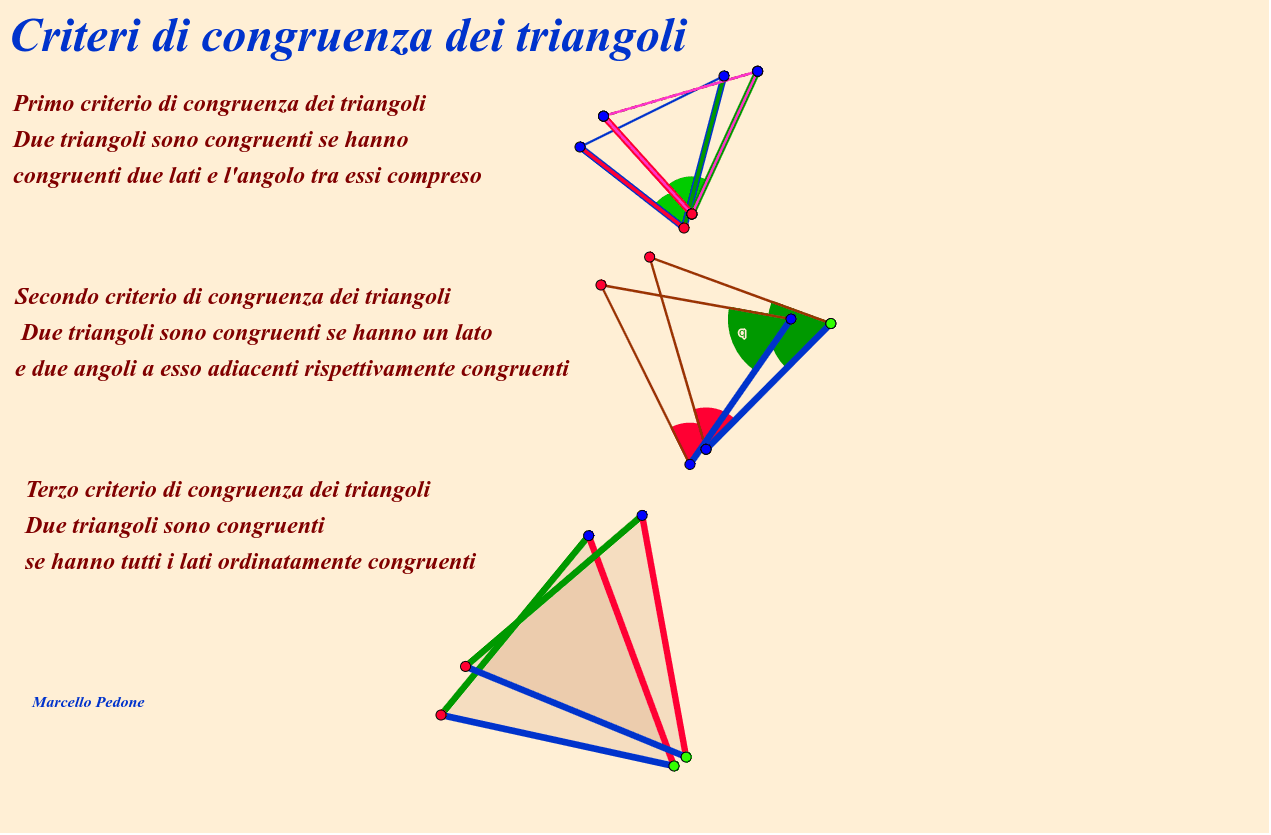
Criterio Di Congruenza Dei Triangoli Rettangoli

Ti sei mai trovato di fronte a due triangoli rettangoli e ti sei chiesto: "Sono esattamente uguali?" Capire quando due figure geometriche sono identiche, o congruenti, è fondamentale non solo in matematica, ma anche in molti aspetti pratici della vita, dall'ingegneria all'architettura. E quando si tratta di triangoli rettangoli, esistono dei criteri specifici che rendono il processo molto più semplice e diretto. Questa guida è pensata per aiutarti a padroneggiare questi criteri, senza dover essere un matematico provetto.

Immagina di dover costruire un tetto. Vuoi assicurarti che i due lati del tetto siano perfettamente identici per garantire stabilità e un aspetto uniforme. I criteri di congruenza dei triangoli rettangoli ti forniscono gli strumenti per farlo con precisione e sicurezza. Continua a leggere e scoprirai come.

Cosa Significa "Congruente"?

Prima di addentrarci nei criteri specifici, è importante definire cosa intendiamo per "congruente". Due figure geometriche sono congruenti se hanno esattamente la stessa forma e le stesse dimensioni. In altre parole, se potessi prendere una delle due figure e sovrapporla all'altra, combacerebbero perfettamente. Per i triangoli, questo significa che tutti i loro lati e tutti i loro angoli corrispondenti sono uguali.

Perché i Triangoli Rettangoli Sono Speciali?

I triangoli rettangoli hanno un angolo retto (90°). Questa caratteristica specifica semplifica la dimostrazione della congruenza rispetto ai triangoli generici. Avere un angolo noto ci permette di concentrarci su un minor numero di elementi per stabilire se due triangoli rettangoli sono congruenti.

I Criteri di Congruenza dei Triangoli Rettangoli

Ecco i criteri principali che utilizzeremo:

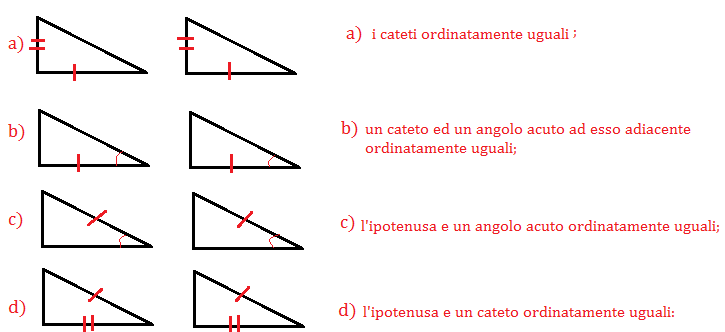
1. Criterio Cateto-Cateto (CC)

Questo criterio è forse il più intuitivo. Afferma che: Se due triangoli rettangoli hanno i cateti corrispondenti congruenti, allora sono congruenti.

Spiegazione: Se i due cateti di un triangolo rettangolo sono uguali ai due cateti corrispondenti di un altro triangolo rettangolo, allora, per il teorema di Pitagora, anche le ipotenuse devono essere uguali. Avendo tre lati uguali (e un angolo retto uguale per definizione), i due triangoli sono necessariamente congruenti.

Esempio: Immagina due triangoli rettangoli. Il primo ha un cateto di 3 cm e l'altro di 4 cm. Il secondo triangolo rettangolo ha anch'esso un cateto di 3 cm e l'altro di 4 cm. In questo caso, possiamo concludere che i due triangoli sono congruenti secondo il criterio CC.

2. Criterio Cateto-Angolo Acuto Adiacente (CA)

Questo criterio afferma che: Se due triangoli rettangoli hanno un cateto e l'angolo acuto adiacente ad esso congruenti, allora sono congruenti.

Spiegazione: Questo criterio si basa sul principio che, in un triangolo, la conoscenza di un lato e due angoli (in questo caso, l'angolo retto e l'angolo acuto adiacente al cateto) determina univocamente il triangolo. Di conseguenza, se abbiamo un cateto e l'angolo acuto adiacente ad esso congruenti, i due triangoli sono congruenti. Questo deriva direttamente dal criterio ALA (Angolo-Lato-Angolo) dei triangoli generici.

Esempio: Considera due triangoli rettangoli. In entrambi, un cateto misura 5 cm, e l'angolo acuto adiacente a questo cateto misura 30°. Allora, i due triangoli sono congruenti secondo il criterio CA.

3. Criterio Cateto-Angolo Acuto Opposto (CO)

Questo criterio afferma che: Se due triangoli rettangoli hanno un cateto e l'angolo acuto opposto ad esso congruenti, allora sono congruenti.

Spiegazione: Se abbiamo un cateto e l'angolo acuto opposto ad esso congruenti, possiamo facilmente calcolare l'altro angolo acuto (essendo la somma degli angoli interni di un triangolo pari a 180°). A questo punto, ci troviamo nella situazione del criterio CA (Cateto-Angolo Acuto Adiacente), e quindi i due triangoli sono congruenti.

Esempio: Immagina due triangoli rettangoli. In entrambi, un cateto misura 6 cm, e l'angolo acuto opposto a questo cateto misura 60°. Allora, i due triangoli sono congruenti secondo il criterio CO.

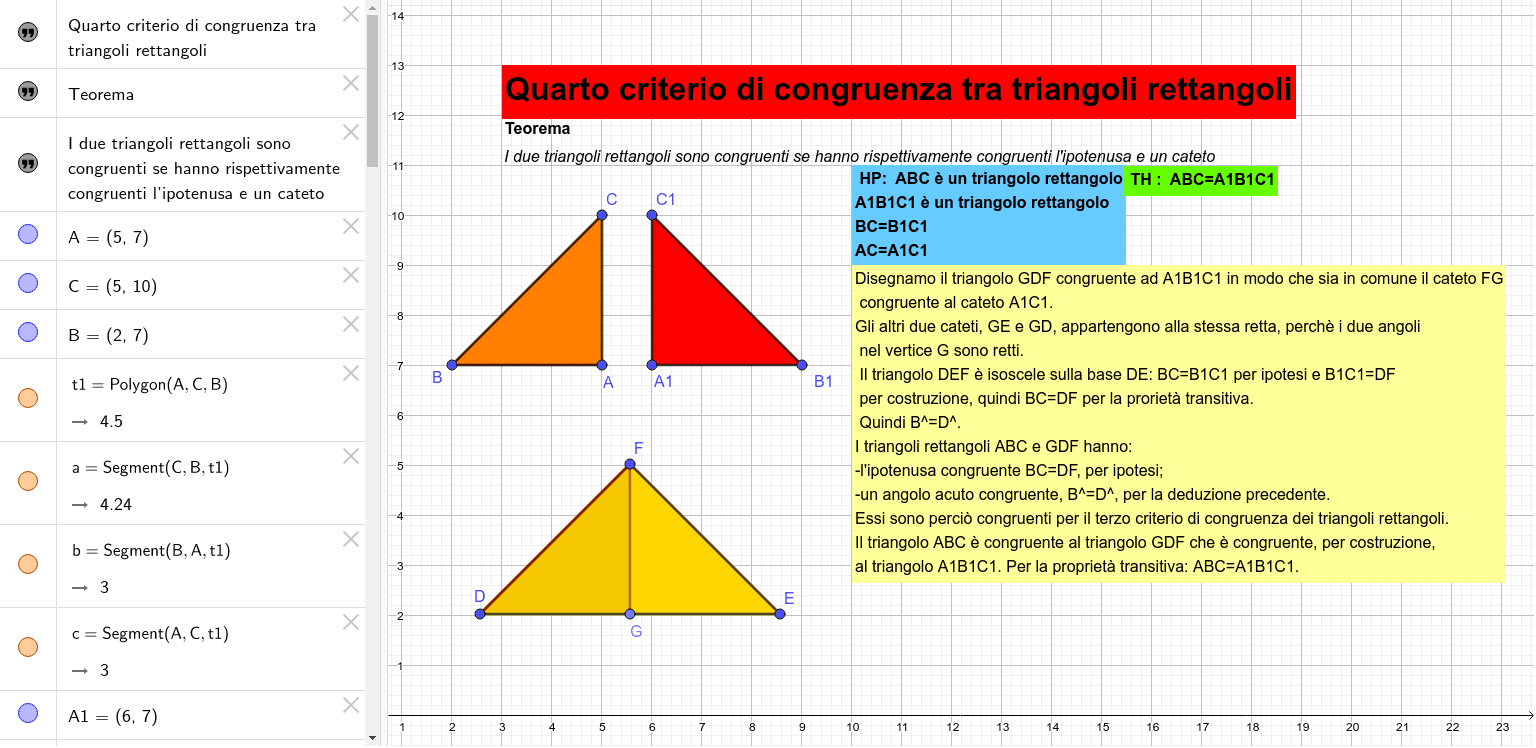
4. Criterio Ipotenusa-Cateto (IC)

Questo criterio afferma che: Se due triangoli rettangoli hanno l'ipotenusa e un cateto congruenti, allora sono congruenti.

Spiegazione: Questo criterio è una conseguenza diretta del teorema di Pitagora. Se conosciamo l'ipotenusa e un cateto, possiamo calcolare l'altro cateto. A quel punto, abbiamo tutti e tre i lati congruenti, e quindi i triangoli sono congruenti per il criterio LLL (Lato-Lato-Lato) dei triangoli generici.

Esempio: Considera due triangoli rettangoli. In entrambi, l'ipotenusa misura 10 cm, e un cateto misura 8 cm. Allora, i due triangoli sono congruenti secondo il criterio IC.

5. Criterio Ipotenusa-Angolo Acuto (IA)

Questo criterio afferma che: Se due triangoli rettangoli hanno l'ipotenusa e un angolo acuto congruenti, allora sono congruenti.

Spiegazione: Se conosciamo l'ipotenusa e un angolo acuto, possiamo calcolare l'altro angolo acuto (essendo la somma degli angoli interni di un triangolo pari a 180°). A questo punto, avendo due angoli uguali (l'angolo acuto dato e l'angolo retto) e un lato uguale (l'ipotenusa), i due triangoli sono simili. Poiché le ipotenuse sono uguali, i triangoli sono congruenti e non solo simili. Più formalmente, questo deriva dal criterio AAA (Angolo-Angolo-Angolo) per la similarità, combinato con la congruenza dell'ipotenusa.

Esempio: Immagina due triangoli rettangoli. In entrambi, l'ipotenusa misura 12 cm, e un angolo acuto misura 45°. Allora, i due triangoli sono congruenti secondo il criterio IA.

Come Applicare i Criteri di Congruenza nella Pratica

Ora che conosci i criteri, vediamo come applicarli in situazioni reali:

1. Identifica i triangoli rettangoli: Assicurati che entrambi i triangoli abbiano un angolo retto. Questo è fondamentale per poter utilizzare questi criteri.
2. Analizza le informazioni disponibili: Cosa sai dei lati e degli angoli dei due triangoli? Prendi nota di tutte le misure che conosci.
3. Scegli il criterio appropriato: In base alle informazioni disponibili, seleziona il criterio che meglio si adatta alla situazione. Ad esempio, se conosci la misura dei due cateti di entrambi i triangoli, usa il criterio Cateto-Cateto (CC).
4. Verifica la congruenza: Assicurati che gli elementi corrispondenti (lati o angoli) siano effettivamente congruenti. Se lo sono, puoi concludere che i triangoli sono congruenti.

Esercizi Pratici

Mettiti alla prova con questi esercizi:

1. Due triangoli rettangoli hanno entrambi un cateto di 7 cm e un angolo acuto adiacente di 55°. Sono congruenti? Quale criterio puoi applicare?
2. Due triangoli rettangoli hanno entrambi un'ipotenusa di 15 cm e un cateto di 9 cm. Sono congruenti? Quale criterio puoi applicare?
3. Un triangolo rettangolo ha un cateto di 4 cm e l'angolo opposto di 30°. Un altro triangolo rettangolo ha un cateto di 4 cm e l'angolo opposto di 60°. Sono congruenti?

Errori Comuni da Evitare

Ecco alcuni errori comuni da evitare quando si applicano i criteri di congruenza dei triangoli rettangoli:

• Confondere i criteri: Assicurati di applicare il criterio corretto in base alle informazioni disponibili.
• Non verificare la corrispondenza: Gli elementi devono essere corrispondenti. Un cateto di un triangolo deve corrispondere al cateto corrispondente dell'altro triangolo.
• Dimenticare l'angolo retto: Ricorda che questi criteri si applicano solo ai triangoli rettangoli.

Conclusione

Comprendere e applicare i criteri di congruenza dei triangoli rettangoli è un'abilità preziosa, non solo in matematica, ma anche in molte discipline pratiche. Con la pratica e l'attenzione ai dettagli, sarai in grado di determinare rapidamente e con precisione se due triangoli rettangoli sono congruenti. Ricorda, la chiave è identificare le informazioni disponibili, scegliere il criterio appropriato e verificare la congruenza degli elementi corrispondenti. Buona fortuna!

Spero che questa guida ti sia stata utile. Ricorda, la matematica è come un muscolo: più la alleni, più forte diventa! Continua a esercitarti e a esplorare le meraviglie della geometria.