Costruzione Di Un Ottagono Dato Il Lato

L'ottagono, un poligono a otto lati, affascina da secoli matematici, architetti e artisti. La sua forma simmetrica e la sua relativa facilità di costruzione lo rendono una figura ricorrente in diverse applicazioni. Questo articolo esplorerà in dettaglio il processo di costruzione di un ottagono regolare quando la lunghezza di un lato è nota. Non ci limiteremo a presentare un metodo, ma analizzeremo le ragioni geometriche che lo sottendono, rendendo la comprensione più profonda e duratura. Preparati a un viaggio nel mondo della geometria e a scoprire la bellezza nascosta in una figura apparentemente semplice.

Fondamenti Teorici: Perché Funziona?

Prima di immergerci nella pratica, è essenziale comprendere i principi teorici che governano la costruzione di un ottagono regolare. Un ottagono regolare è caratterizzato da due proprietà fondamentali: tutti i suoi lati hanno la stessa lunghezza e tutti i suoi angoli interni sono uguali. Questa regolarità è cruciale per la nostra costruzione.

Angoli Interni e Angoli al Centro

La somma degli angoli interni di un poligono con n lati è data dalla formula (n-2) * 180°. Nel caso dell'ottagono (n=8), questa somma è (8-2) * 180° = 1080°. Poiché l'ottagono è regolare, ogni angolo interno misura 1080°/8 = 135°. Questo valore è fondamentale per guidare la nostra costruzione.

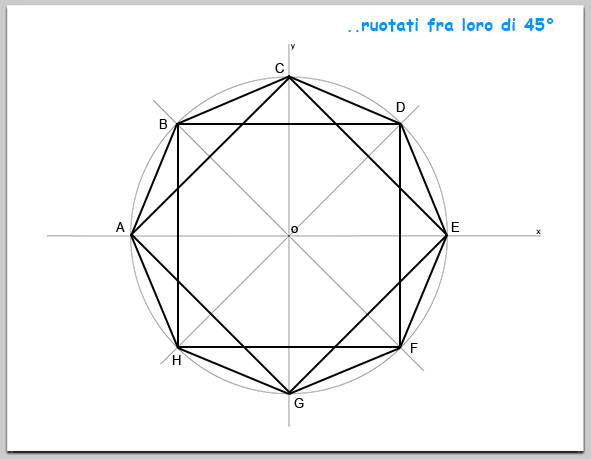
Un altro concetto importante è l'angolo al centro. Se immaginiamo di dividere l'ottagono in otto triangoli congruenti, con un vertice al centro dell'ottagono, l'angolo al centro di ciascun triangolo è 360°/8 = 45°. Questo angolo ci aiuta a determinare come i lati dell'ottagono si irradiano dal centro.

Relazione tra Lato e Raggio del Cerchio Circoscritto

La costruzione che presenteremo si basa sulla relazione tra il lato dell'ottagono e il raggio del cerchio circoscritto. Il cerchio circoscritto è il cerchio che passa per tutti i vertici dell'ottagono. Esiste una formula che collega la lunghezza del lato (l) e il raggio (r) del cerchio circoscritto: l = r * √(2 - √2). Questa formula può essere derivata dalla trigonometria e dalle proprietà dei triangoli isosceli formati dai lati dell'ottagono e dai raggi del cerchio circoscritto. Tuttavia, per la costruzione pratica, non è necessario memorizzare questa formula; i passaggi che seguiranno la incorporano implicitamente.

Costruzione Passo Dopo Passo

Ora che abbiamo compreso la teoria, possiamo procedere con la costruzione pratica dell'ottagono regolare dato il lato. Useremo un compasso, una riga (o squadra) e una matita. La precisione è fondamentale per ottenere un risultato ottimale.

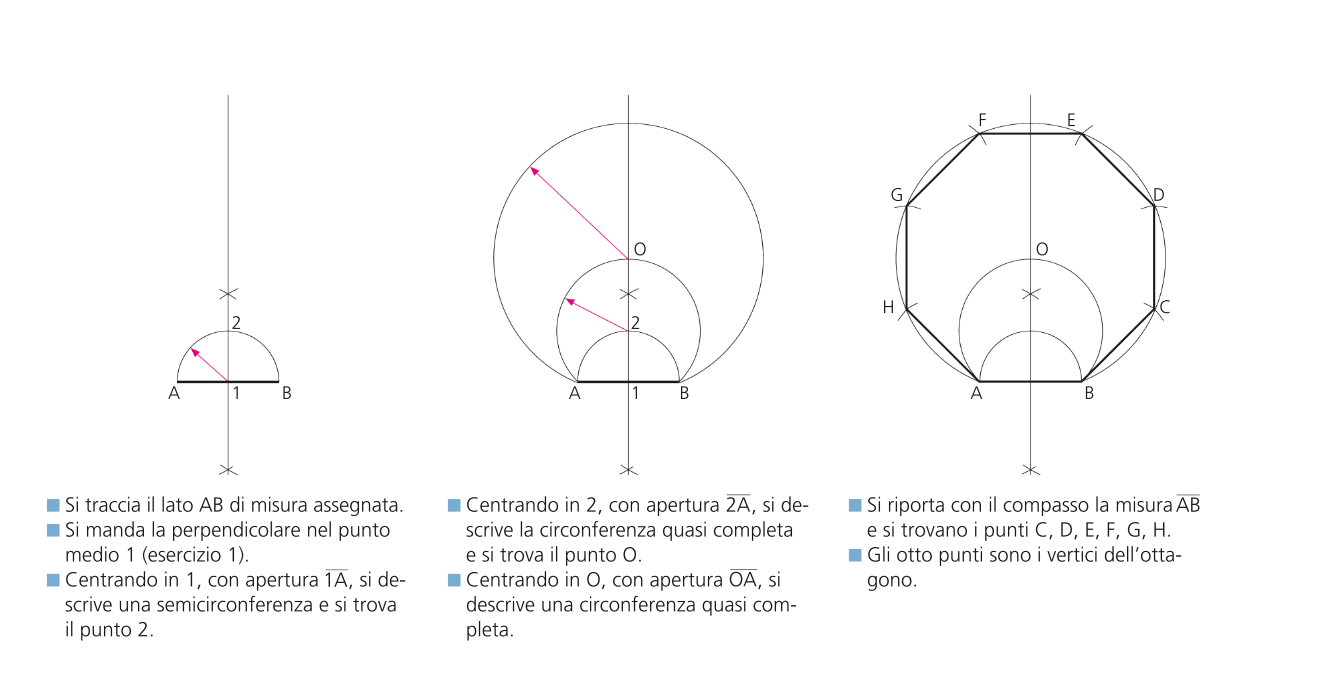
Passo 1: Disegnare il Lato Dato

Inizia disegnando il lato dell'ottagono che ti è stato fornito. Chiama gli estremi di questo segmento A e B. Questo segmento AB rappresenterà uno degli otto lati del nostro ottagono.

Passo 2: Costruire le Perpendicolari agli Estremi del Lato

Costruisci le rette perpendicolari al segmento AB nei punti A e B. Questo può essere fatto utilizzando un compasso e una riga, o semplicemente utilizzando una squadra. Assicurati che le rette siano perfettamente perpendicolari; un piccolo errore qui si propagherà durante tutta la costruzione.

Passo 3: Determinare la Lunghezza della Diagonale del Quadrato che Contiene il Lato

Prendi la lunghezza del lato AB con il compasso. Con il compasso puntato in A, traccia un arco che interseca la perpendicolare in A. Chiama il punto di intersezione C. Ripeti lo stesso procedimento con il compasso puntato in B, intersecando la perpendicolare in B. Chiama il punto di intersezione D. AC e BD avranno la stessa lunghezza del lato AB.

Passo 4: Trovare il Centro dei Due Lati Adiacenti

Ora, con il compasso ancora aperto con la stessa apertura AB, punta il compasso in C e traccia un arco che interseca la retta AC. Chiama il punto di intersezione E. Fai lo stesso partendo da D e intersecando la retta BD. Chiama il punto di intersezione F. I segmenti AE e BF avranno la lunghezza della diagonale del quadrato che contiene i lati AB, AC e BD.

Passo 5: Trovare il Centro dell'Ottagono

Unisci i punti E e F con una retta. Trova il punto medio M del segmento EF. Il punto M sarà il centro del nostro ottagono.

Passo 6: Disegnare il Cerchio Circoscritto

Con il compasso puntato in M e un'apertura pari alla distanza MA (o MB), traccia un cerchio. Questo è il cerchio circoscritto all'ottagono. Dovrebbe passare per i punti A e B.

Passo 7: Trovare gli Altri Vertici dell'Ottagono

Mantieni la stessa apertura del compasso pari alla lunghezza del lato AB. Punta il compasso in B e traccia un arco che interseca il cerchio circoscritto. Chiama il punto di intersezione G. Ripeti questo processo partendo da G per trovare il prossimo vertice, e così via, finché non avrai otto vertici in totale sul cerchio. Assicurati che la distanza tra ogni vertice sia sempre pari alla lunghezza del lato AB.

Passo 8: Collegare i Vertici per Formare l'Ottagono

Collega in sequenza tutti gli otto vertici trovati sul cerchio circoscritto. Otterrai un ottagono regolare il cui lato ha la lunghezza specificata inizialmente.

Consigli per la Precisione

Come già accennato, la precisione è cruciale in questa costruzione. Ecco alcuni consigli per migliorare l'accuratezza:

• Utilizza un compasso di buona qualità che mantenga la sua apertura.
• Affila la matita regolarmente per ottenere linee sottili e precise.
• Sii paziente e controlla attentamente ogni passo.
• Se hai dubbi, ripeti il passo per assicurarti di averlo eseguito correttamente.

Applicazioni Pratiche

Gli ottagoni non sono solo figure geometriche astratte; si trovano in molte applicazioni del mondo reale. Ecco alcuni esempi:

• Architettura: Gli ottagoni sono usati in piante di edifici, cupole e torri. Un esempio famoso è il Battistero di Firenze.
• Design: La forma ottagonale si trova in segnali stradali (come il segnale di stop), bottoni, e altri oggetti di uso quotidiano.
• Ingegneria: Alcuni dadi e bulloni sono ottagonali per consentire l'applicazione di una coppia maggiore.
• Arte e Artigianato: Gli ottagoni possono essere usati per creare mosaici, quilting e altre forme di arte decorativa.

L'uso dell'ottagono nei segnali di stop è un esempio particolarmente significativo. La sua forma unica lo rende immediatamente riconoscibile anche in condizioni di scarsa visibilità, aumentando la sicurezza stradale.

Conclusioni

La costruzione di un ottagono regolare dato il lato è un esercizio affascinante che combina la teoria geometrica con la pratica. Sebbene possa sembrare complesso all'inizio, seguendo i passaggi attentamente e prestando attenzione alla precisione, chiunque può creare un ottagono perfetto. Speriamo che questo articolo ti abbia fornito una comprensione chiara e completa del processo, non solo come farlo, ma anche perché funziona. Ora tocca a te! Prendi un compasso, una riga e una matita e mettiti alla prova. La soddisfazione di creare una figura geometrica perfetta è un'esperienza gratificante e un ottimo modo per apprezzare la bellezza e l'eleganza della matematica.