Come Trovo La Diagonale Di Un Quadrato

Calcolare la diagonale di un quadrato è un'operazione fondamentale in geometria, che trova applicazioni in diversi campi, dalla costruzione all'arte. Questo articolo esplora i metodi per determinare la diagonale di un quadrato, spiegando il ragionamento matematico alla base e fornendo esempi pratici.
Metodi per Calcolare la Diagonale di un Quadrato
Esistono principalmente due approcci per calcolare la diagonale di un quadrato: utilizzando il Teorema di Pitagora e applicando una formula diretta.
Il Teorema di Pitagora
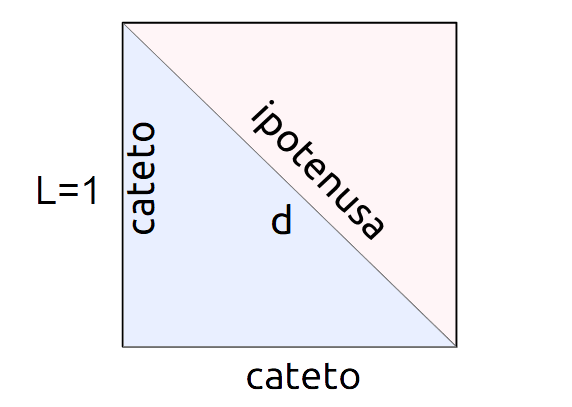
Il Teorema di Pitagora è un pilastro della geometria euclidea e afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti). Un quadrato può essere diviso in due triangoli rettangoli congruenti tracciando la sua diagonale. In questo caso, la diagonale diventa l'ipotenusa, mentre i lati del quadrato diventano i cateti.
Se l è la lunghezza di un lato del quadrato e d è la lunghezza della diagonale, possiamo applicare il Teorema di Pitagora come segue:
d2 = l2 + l2
d2 = 2l2
d = √(2l2)
d = l√2
Quindi, la diagonale di un quadrato è uguale alla lunghezza del suo lato moltiplicata per la radice quadrata di 2.
Esempio: Se un quadrato ha un lato di 5 cm, la sua diagonale sarà 5√2 cm, che approssimativamente è 7.07 cm.
La Formula Diretta
Come derivato dal Teorema di Pitagora, esiste una formula diretta che semplifica il calcolo della diagonale. La formula è:
d = l√2
Dove d è la diagonale e l è la lunghezza del lato del quadrato. Questa formula è particolarmente utile quando si ha bisogno di calcolare rapidamente la diagonale senza passare per i passaggi del Teorema di Pitagora.
Esempio: Se un quadrato ha un lato di 10 metri, la sua diagonale sarà 10√2 metri, che approssimativamente è 14.14 metri.
Applicazioni Pratiche
Il calcolo della diagonale di un quadrato ha numerose applicazioni pratiche in diverse discipline:
*Costruzioni Edili: Gli architetti e gli ingegneri utilizzano questo calcolo per determinare le dimensioni di pavimenti, stanze e altri elementi strutturali che hanno forme quadrate. Ad esempio, per assicurarsi che una stanza sia perfettamente quadrata, possono misurare le diagonali e verificarne l'uguaglianza.
*Design e Arte: Nel design grafico e nell'arte, la diagonale di un quadrato può essere utilizzata per creare composizioni equilibrate e proporzioni armoniose. La sezione aurea, spesso utilizzata nell'arte, è strettamente legata alle proprietà geometriche dei quadrati e dei rettangoli, inclusa la diagonale.
*Geometria e Matematica: Il concetto di diagonale è fondamentale nello studio della geometria e della matematica. Viene utilizzato per dimostrare teoremi, risolvere problemi e comprendere le relazioni tra le diverse figure geometriche.
*Cartografia: Nella creazione di mappe, il calcolo delle diagonali aiuta a determinare le distanze tra i punti e a mantenere la precisione delle rappresentazioni geografiche, specialmente quando si utilizzano coordinate cartesiane.
*Giochi e Puzzle: Molti giochi e puzzle, come i tangram o i puzzle di logica, si basano sulla manipolazione di forme geometriche, inclusi i quadrati, e la comprensione delle loro proprietà, come la diagonale, è essenziale per risolverli.
*Elettronica: Nel design di circuiti stampati e dispositivi elettronici, il calcolo delle diagonali può essere importante per ottimizzare il posizionamento dei componenti e garantire un layout efficiente.
Esempio Dettagliato con Dati Reali
Immaginiamo di dover pavimentare una stanza quadrata con piastrelle di forma triangolare rettangola isoscele. La stanza ha un lato di 4 metri. Vogliamo determinare quanto è lunga la diagonale della stanza, poiché potremmo voler posizionare un mobile lungo questa linea.
1. Identifichiamo il lato: l = 4 metri.
2. Applichiamo la formula: d = l√2
3. Sostituiamo il valore: d = 4√2 metri
4. Calcoliamo la radice quadrata di 2: √2 ≈ 1.414
5. Moltiplichiamo: d ≈ 4 * 1.414 = 5.656 metri
Quindi, la diagonale della stanza è approssimativamente 5.656 metri. Questo ci permette di pianificare l'arredamento sapendo la dimensione massima di un mobile che può essere posizionato lungo la diagonale.
Ora, immaginiamo di dover tagliare un pezzo di tessuto di forma quadrata per un progetto di quilting. Sappiamo che la diagonale del quadrato deve essere di 30 cm. Quanto deve essere lungo il lato del quadrato?
1. Conosciamo la diagonale: d = 30 cm
2. Utilizziamo la formula (inversione): l = d / √2
3. Sostituiamo il valore: l = 30 / √2 cm
4. Calcoliamo la radice quadrata di 2: √2 ≈ 1.414
5. Dividiamo: l ≈ 30 / 1.414 ≈ 21.21 cm
Quindi, il lato del quadrato deve essere approssimativamente 21.21 cm.
Considerazioni Importanti
Quando si calcola la diagonale di un quadrato, è importante considerare le seguenti cose:
*Unità di Misura: Assicurarsi che tutte le misure siano espresse nella stessa unità. Se il lato è misurato in centimetri, la diagonale sarà in centimetri. Se il lato è misurato in metri, la diagonale sarà in metri.
*Approssimazioni: La radice quadrata di 2 è un numero irrazionale, il che significa che ha infinite cifre decimali non ripetitive. Quando si calcola la diagonale, è spesso necessario approssimare √2 a un certo numero di cifre decimali (ad esempio, 1.414). Questo introduce un piccolo errore di approssimazione, che può essere trascurabile nella maggior parte delle applicazioni pratiche.
*Precisione: A seconda dell'applicazione, potrebbe essere necessario calcolare la diagonale con un alto grado di precisione. In questi casi, è consigliabile utilizzare una calcolatrice scientifica o un software matematico che può gestire numeri irrazionali con maggiore precisione.
Conclusione
Calcolare la diagonale di un quadrato è un'operazione semplice ma potente, che si basa su principi fondamentali della geometria. Che si utilizzi il Teorema di Pitagora o la formula diretta, la comprensione di questo concetto permette di risolvere una varietà di problemi pratici in diversi ambiti. Sperimentate con diversi valori e provate ad applicare queste conoscenze in situazioni reali. La geometria è ovunque intorno a noi, e imparare a comprenderla ci aiuta a interagire meglio con il mondo che ci circonda. Non smettete mai di imparare!