Come Trovare L'ipotenusa Avendo I Cateti

Capita a tutti di bloccarsi di fronte a un problema di matematica. A volte, anche concetti che sembrano semplici, come trovare l'ipotenusa di un triangolo rettangolo, possono creare confusione. Niente panico! La matematica è un linguaggio che si impara, un passo alla volta. In questo articolo, ti guiderò attraverso il processo, rendendolo chiaro e accessibile. Vedrai che, con la giusta spiegazione, ce la farai!

Cos'è l'ipotenusa e perché è importante?

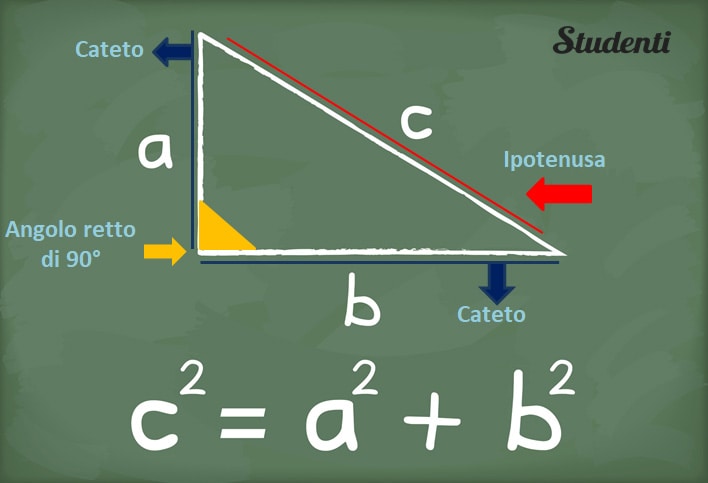
Partiamo dalle basi. Un triangolo rettangolo è un triangolo che ha un angolo di 90 gradi (un angolo retto). I due lati che formano l'angolo retto si chiamano cateti, mentre il lato opposto all'angolo retto è l'ipotenusa.

L'ipotenusa è il lato più lungo del triangolo rettangolo. Ma perché è così importante? Perché la sua lunghezza ci permette di risolvere una miriade di problemi in geometria, fisica e ingegneria. Immagina di dover calcolare la distanza più breve tra due punti su una mappa, oppure di dover progettare una rampa: la conoscenza dell'ipotenusa è fondamentale!

Il Teorema di Pitagora: la chiave per trovare l'ipotenusa

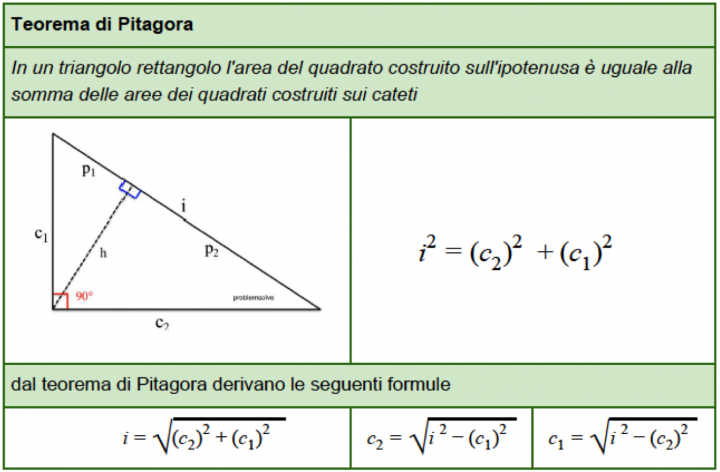
Il Teorema di Pitagora è il vero protagonista della nostra storia. Formulato dal matematico greco Pitagora (circa 570-495 a.C.), questo teorema afferma che in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.

In termini matematici, questo si traduce in: a² + b² = c²

Dove:

• a e b sono le lunghezze dei cateti
• c è la lunghezza dell'ipotenusa

Questo teorema è universale e valido per tutti i triangoli rettangoli. La sua applicazione è vastissima, e la sua comprensione è un pilastro fondamentale della geometria.

Come applicare il Teorema di Pitagora per trovare l'ipotenusa

Ora che abbiamo capito il Teorema di Pitagora, vediamo come usarlo concretamente per calcolare l'ipotenusa.

1. Identifica i cateti: Assicurati di conoscere le lunghezze dei due cateti (a e b).
2. Eleva al quadrato i cateti: Calcola a² e b².
3. Somma i quadrati: Somma i risultati ottenuti al punto precedente (a² + b²).
4. Calcola la radice quadrata: Trova la radice quadrata della somma ottenuta. Questo risultato è la lunghezza dell'ipotenusa (c).

In formula: c = √(a² + b²)

Esempio pratico:

Supponiamo che un triangolo rettangolo abbia cateti di lunghezza a = 3 cm e b = 4 cm. Calcoliamo l'ipotenusa:

1. a² = 3² = 9
2. b² = 4² = 16
3. a² + b² = 9 + 16 = 25
4. c = √25 = 5

Quindi, l'ipotenusa del triangolo è lunga 5 cm.

Trucchi e consigli per non sbagliare

• Attenzione alle unità di misura: Assicurati che i cateti siano misurati nella stessa unità di misura prima di applicare il teorema. Se uno è in metri e l'altro in centimetri, dovrai convertirli.
• Usa la calcolatrice: Per calcolare la radice quadrata, usa una calcolatrice scientifica. Questo ti eviterà errori di calcolo.
• Verifica il risultato: Ricorda che l'ipotenusa è sempre il lato più lungo del triangolo rettangolo. Se il risultato che ottieni è inferiore alla lunghezza di uno dei cateti, hai commesso un errore.
• Visualizza il problema: Disegna sempre un triangolo rettangolo e scrivi le lunghezze dei cateti. Questo ti aiuterà a visualizzare il problema e a non confonderti.

Come aiutare i bambini e gli studenti a comprendere il Teorema di Pitagora

Insegnare il Teorema di Pitagora può essere una sfida, ma ci sono diverse strategie che possono rendere l'apprendimento più efficace e divertente.

• Usa materiale manipolativo: Costruisci triangoli rettangoli con cartoncino o legno e ritaglia quadrati che abbiano i lati della stessa lunghezza dei cateti e dell'ipotenusa. Questo aiuterà i bambini a visualizzare la relazione tra le aree dei quadrati.
• Racconta la storia di Pitagora: Raccontare la storia del matematico Pitagora e del suo teorema può rendere l'argomento più interessante e coinvolgente.
• Utilizza esempi concreti: Collega il Teorema di Pitagora a situazioni reali, come calcolare la lunghezza di una scala appoggiata a un muro o la diagonale di un campo da calcio.
• Giochi e attività interattive: Esistono molti giochi online e app che aiutano a imparare il Teorema di Pitagora in modo divertente e interattivo.
• Lavora in gruppo: Organizza attività di gruppo in cui gli studenti devono risolvere problemi applicando il Teorema di Pitagora. Questo favorirà la collaborazione e l'apprendimento reciproco.

Secondo la ricerca in didattica della matematica, l'apprendimento è più efficace quando è attivo e coinvolgente. L'utilizzo di materiale manipolativo e di esempi concreti aiuta gli studenti a costruire una comprensione profonda del Teorema di Pitagora.

Oltre il triangolo rettangolo: le applicazioni avanzate

Il Teorema di Pitagora non si limita al calcolo dell'ipotenusa di un triangolo rettangolo. Ha applicazioni molto più ampie in diversi campi:

• Navigazione: Utilizzato per calcolare distanze e rotte.
• Architettura e ingegneria: Fondamentale per la progettazione di edifici, ponti e altre strutture.
• Fisica: Utilizzato per calcolare la risultante di vettori.
• Grafica computerizzata: Utilizzato per calcolare distanze e angoli in grafica 3D.

La sua comprensione apre le porte a una maggiore comprensione del mondo che ci circonda.

Conclusione: un teorema, infinite possibilità

Il Teorema di Pitagora è molto più di una semplice formula matematica. È uno strumento potente che ci permette di risolvere problemi reali e di comprendere il mondo che ci circonda. Non lasciarti intimorire dalla matematica! Con un po' di impegno e la giusta guida, puoi superare qualsiasi ostacolo. Ricorda: la matematica è come una scalata: un passo alla volta, raggiungerai la cima!

Spero che questo articolo ti sia stato utile. Non esitare a rileggerlo e a fare esercizi per mettere in pratica ciò che hai imparato. Buono studio!