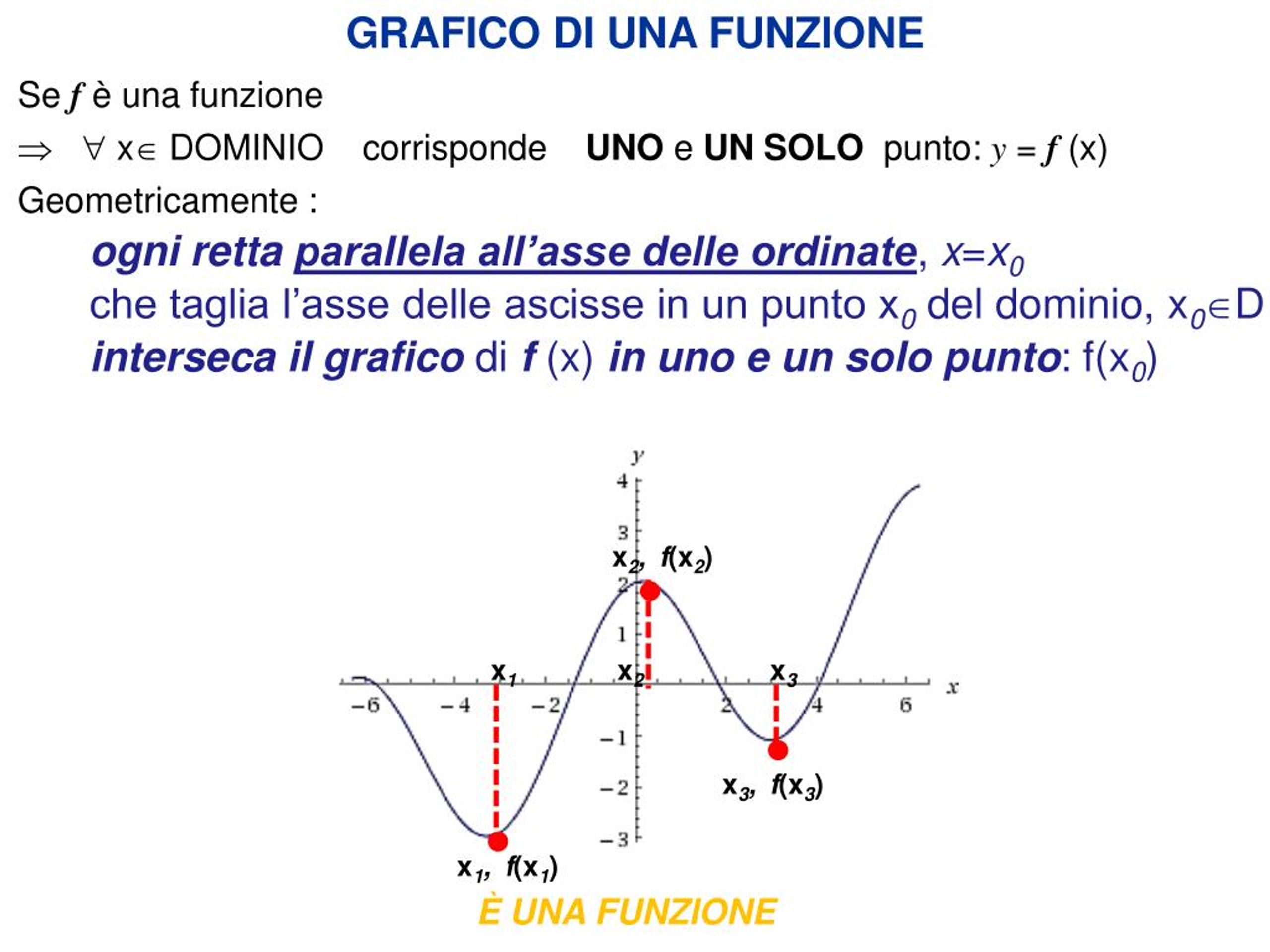
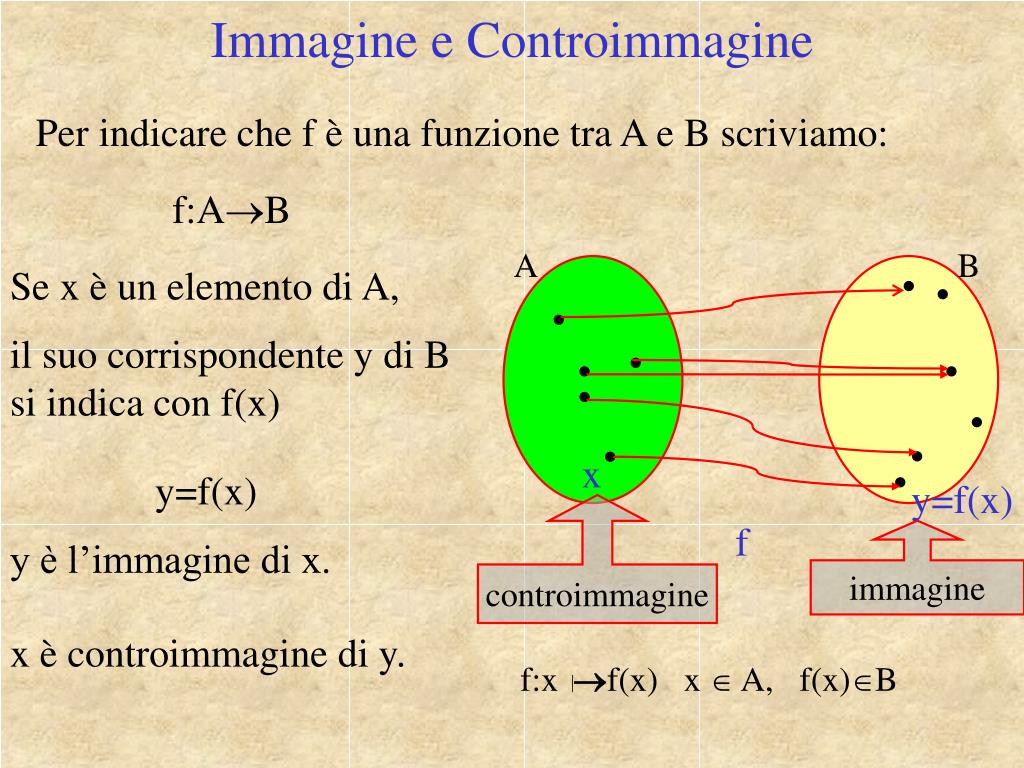
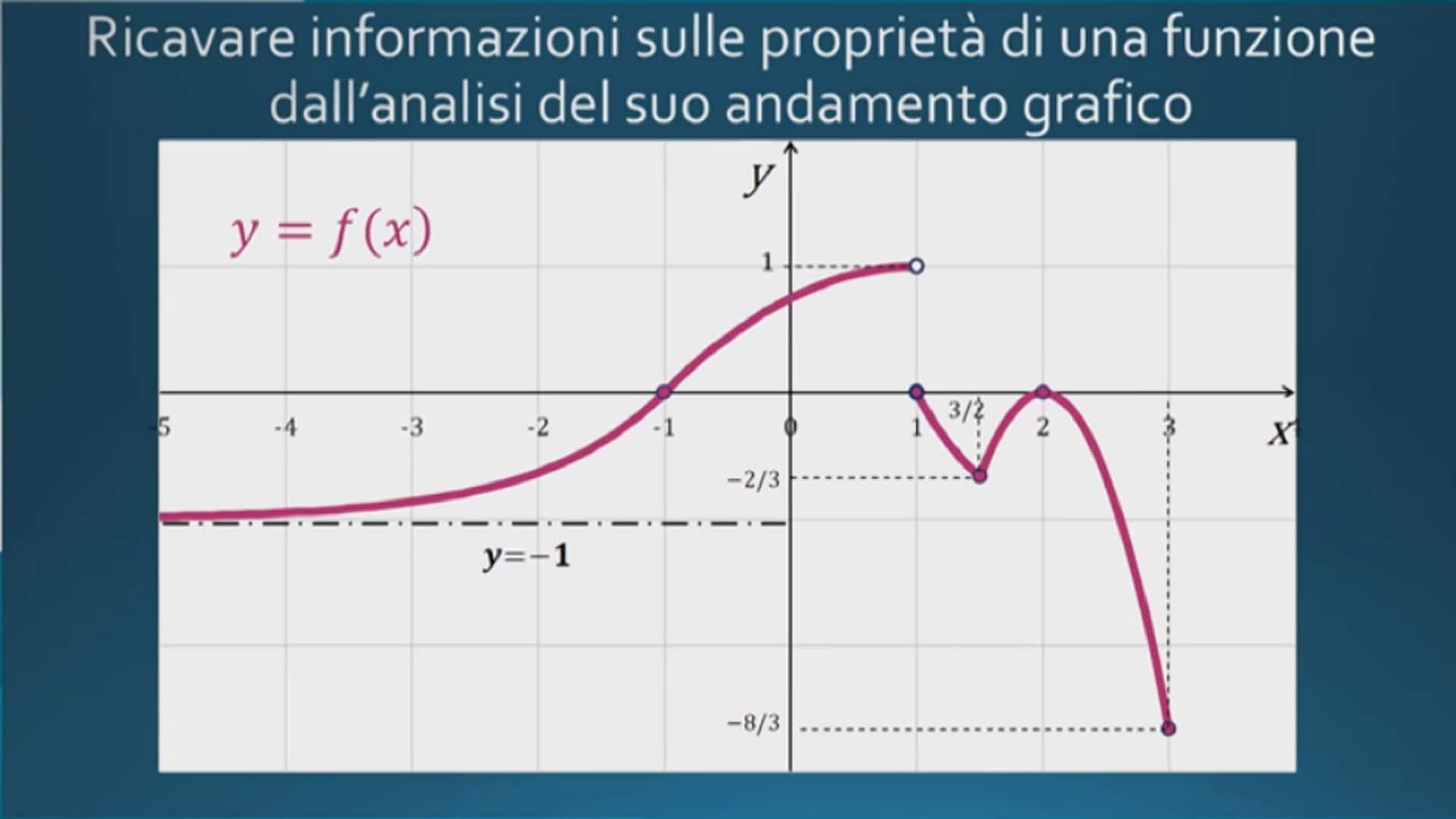
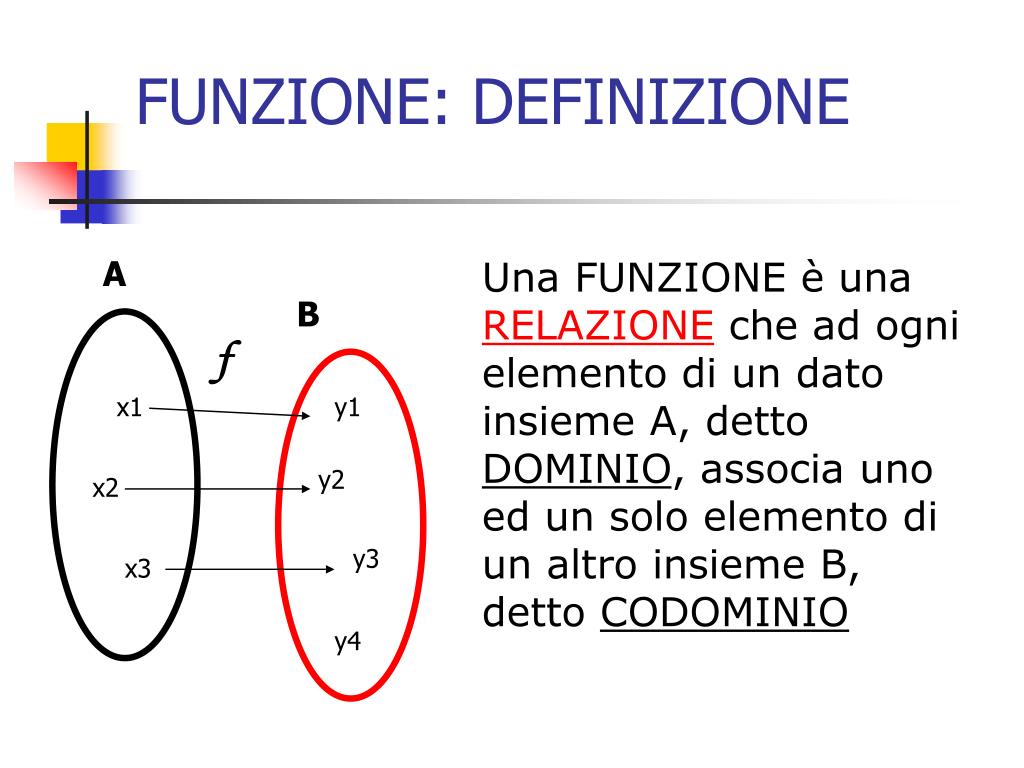
Come Trovare L Immagine Di Una Funzione

L'immagine di una funzione, spesso indicata come codominio o range, rappresenta l'insieme di tutti i valori che la funzione può effettivamente assumere. Trovare l'immagine è fondamentale per comprendere appieno il comportamento di una funzione e le sue limitazioni. Si tratta di determinare quali valori di output sono raggiungibili a partire da un dato insieme di input (il dominio).
Che cos'è l'Immagine di una Funzione?
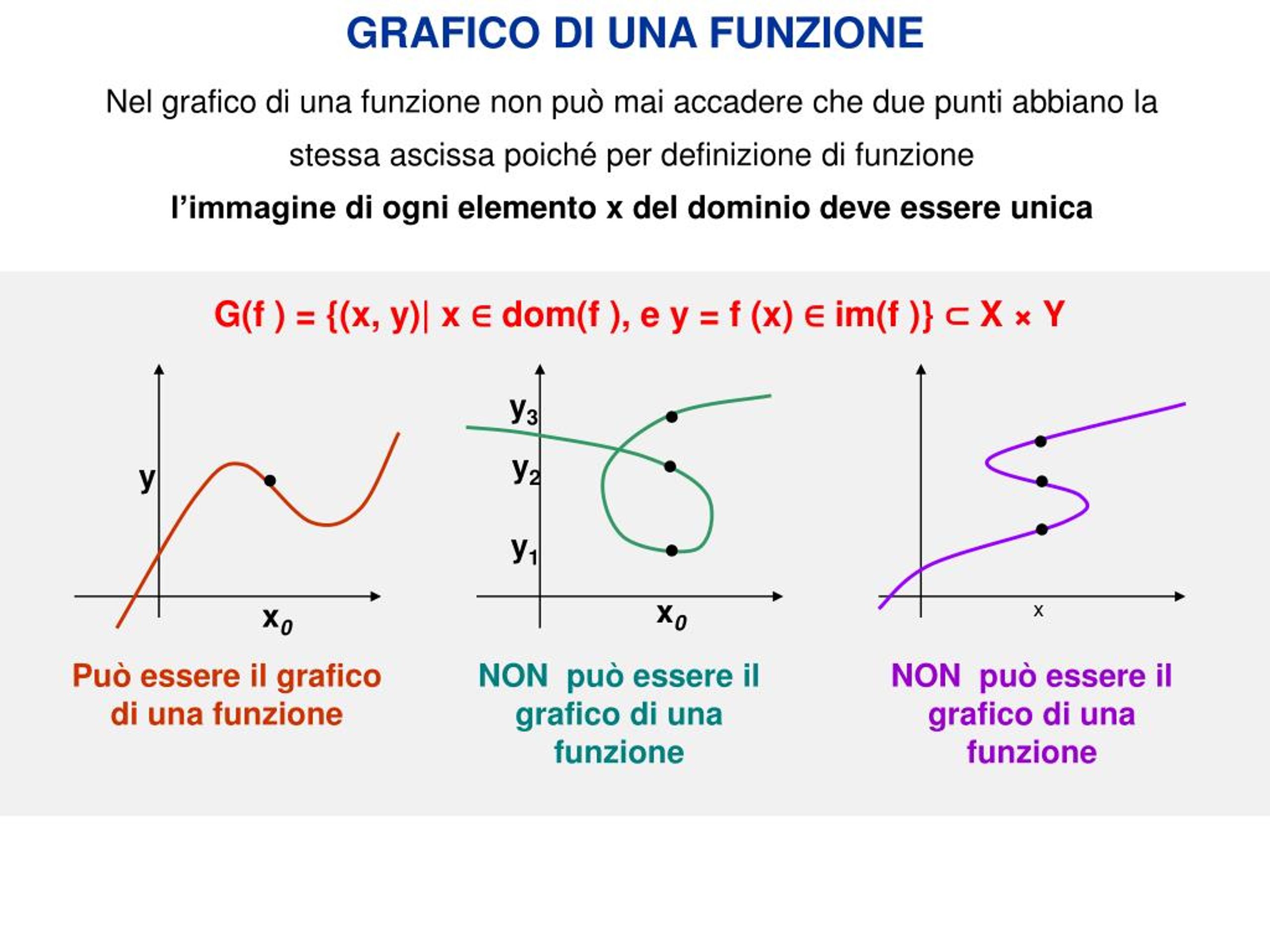
Formalmente, data una funzione f(x), l'immagine è l'insieme di tutti i valori y tali che y = f(x) per qualche x nel dominio di f. In altre parole, è l'insieme di tutti i risultati che si ottengono applicando la funzione a tutti gli elementi del suo dominio. Determinare l'immagine implica analizzare come la funzione trasforma i valori di input nei valori di output e identificare l'intervallo di valori che vengono effettivamente prodotti.
Perché è Importante?
Comprendere l'immagine di una funzione è cruciale per diversi motivi, specialmente nel contesto dell'apprendimento matematico e delle sue applicazioni:
- Risoluzione di equazioni: Conoscere l'immagine di una funzione aiuta a determinare se un'equazione ha soluzioni. Se il valore che si cerca di ottenere non rientra nell'immagine della funzione, allora l'equazione non ammette soluzioni.
- Grafici di funzioni: L'immagine fornisce informazioni essenziali per la corretta rappresentazione grafica di una funzione. Indica l'estensione verticale del grafico, contribuendo a definire la scala appropriata per gli assi.
- Applicazioni pratiche: Molti problemi reali possono essere modellati attraverso funzioni. La conoscenza dell'immagine permette di interpretare i risultati ottenuti in termini di grandezze fisiche, economiche o di altro tipo, assicurando che le soluzioni siano realistiche e significative.
Come Trovare l'Immagine: Metodi e Tecniche
Esistono diversi approcci per determinare l'immagine di una funzione, a seconda della sua complessità e delle sue caratteristiche. Alcuni metodi comuni includono:
"La comprensione del dominio e dell'immagine di una funzione è fondamentale per interpretare i risultati matematici in un contesto del mondo reale." - Prof.ssa Maria Rossi, Dipartimento di Matematica, Università degli Studi di Milano.
- Analisi diretta: In alcuni casi, è possibile dedurre l'immagine semplicemente analizzando la funzione. Ad esempio, se f(x) = x2, si sa che l'immagine sarà l'insieme di tutti i numeri reali non negativi, poiché il quadrato di un numero reale è sempre non negativo.
- Studio della derivata (per funzioni continue): La derivata di una funzione fornisce informazioni sulla sua crescenza e decrescenza. Trovando i punti di massimo e minimo locali, si può determinare l'intervallo di valori che la funzione assume.
- Trasformazioni di funzioni note: Se la funzione è ottenuta tramite trasformazioni (traslazioni, dilatazioni, riflessioni) di una funzione di cui si conosce l'immagine, si può determinare l'immagine della funzione trasformata applicando le stesse trasformazioni all'immagine originale.
- Utilizzo di grafici: Un grafico accurato della funzione può fornire un'indicazione visiva dell'immagine. Basta osservare l'intervallo di valori sull'asse y coperto dal grafico.
- Metodi algebrici: Per alcune funzioni, è possibile trovare l'immagine risolvendo l'equazione y = f(x) rispetto a x. Se si riesce a esprimere x in funzione di y, si può determinare per quali valori di y esiste una soluzione x nel dominio di f.
Applicazioni Pratiche per gli Studenti
La comprensione dell'immagine di una funzione ha implicazioni dirette nella vita scolastica degli studenti:
- Fisica: Nel calcolo della gittata di un proiettile, l'immagine della funzione che descrive la traiettoria aiuta a determinare l'altezza massima raggiunta.
- Economia: Nello studio di una funzione di costo, l'immagine indica l'intervallo di costi possibili per un determinato livello di produzione.
- Informatica: Nella programmazione, conoscere l'immagine di una funzione è essenziale per validare i risultati di un algoritmo e assicurarsi che rientrino in un intervallo accettabile.
Inoltre, la capacità di determinare l'immagine di una funzione sviluppa il pensiero critico e la capacità di problem solving, competenze preziose in qualsiasi ambito della vita.