Come Trovare L Area Del Triangolo

Capita a tutti di sentirsi un po' persi di fronte alla geometria, soprattutto quando si tratta di calcolare l'area di figure complesse come il triangolo. Niente panico! Molti studenti si trovano nella stessa situazione. L'importante è affrontare il problema con metodo e comprensione. Questo articolo ti guiderà passo dopo passo, rendendo il calcolo dell'area del triangolo un gioco da ragazzi. Non solo ti forniremo le formule, ma ti spiegheremo perché funzionano e come applicarle in diversi contesti. Ricorda, l'apprendimento è un percorso, e siamo qui per aiutarti a percorrerlo con successo!

Comprendere le Basi: Cos'è un Triangolo?

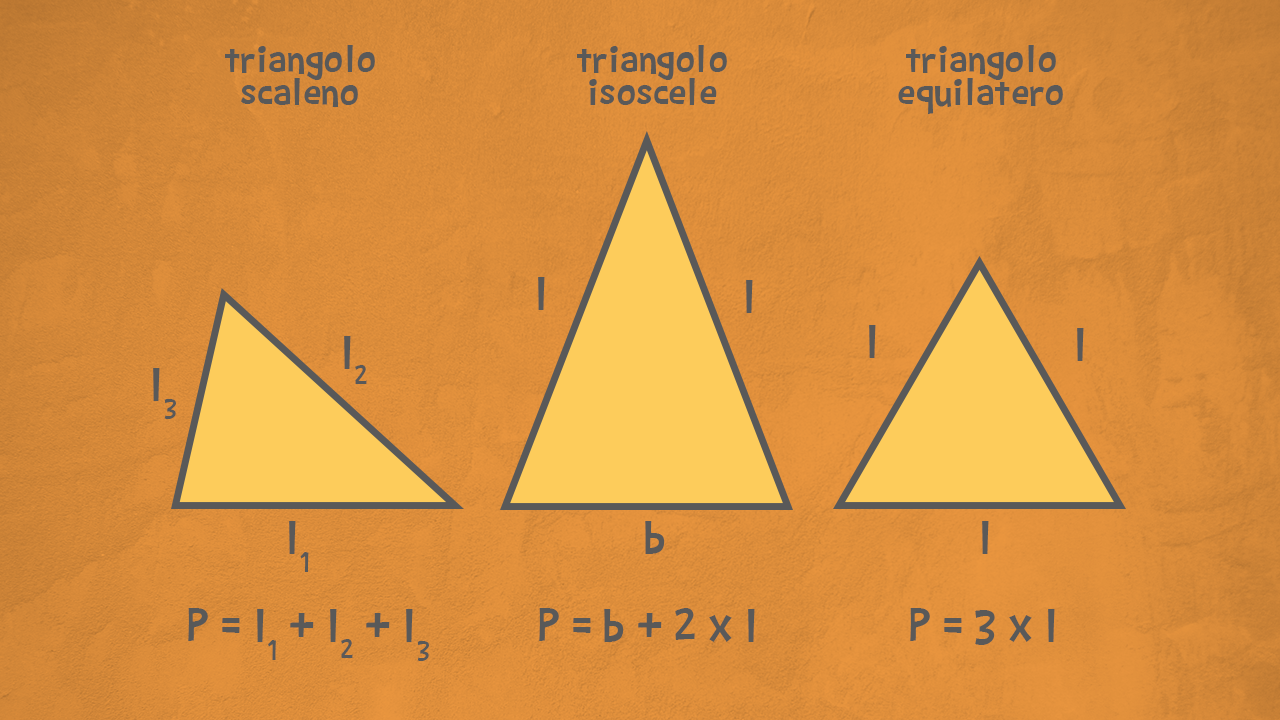
Prima di addentrarci nel calcolo dell'area, ripassiamo rapidamente cosa rende un triangolo un triangolo. Un triangolo è una figura geometrica con tre lati e tre angoli. La somma degli angoli interni di un triangolo è sempre 180 gradi. Esistono diversi tipi di triangoli, classificati in base ai loro lati e angoli:

• Equilatero: Tre lati uguali, tre angoli uguali (60 gradi ciascuno).
• Isoscele: Due lati uguali, due angoli uguali.
• Scaleno: Tutti i tre lati di lunghezza diversa, tutti gli angoli diversi.
• Rettangolo: Ha un angolo retto (90 gradi). Il lato opposto all'angolo retto è chiamato ipotenusa.
• Ottusangolo: Ha un angolo ottuso (maggiore di 90 gradi).
• Acutangolo: Tutti gli angoli sono acuti (minori di 90 gradi).

Conoscere queste distinzioni è fondamentale, perché a volte il tipo di triangolo può influenzare la scelta della formula più adatta per calcolarne l'area.

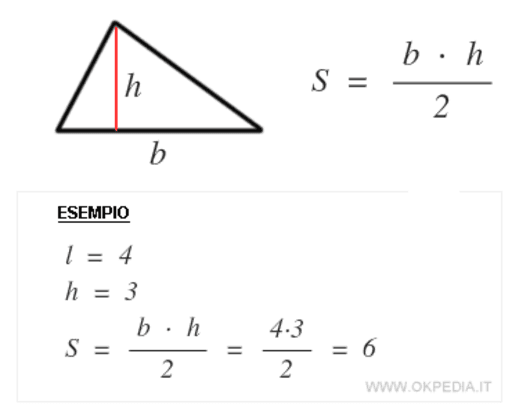
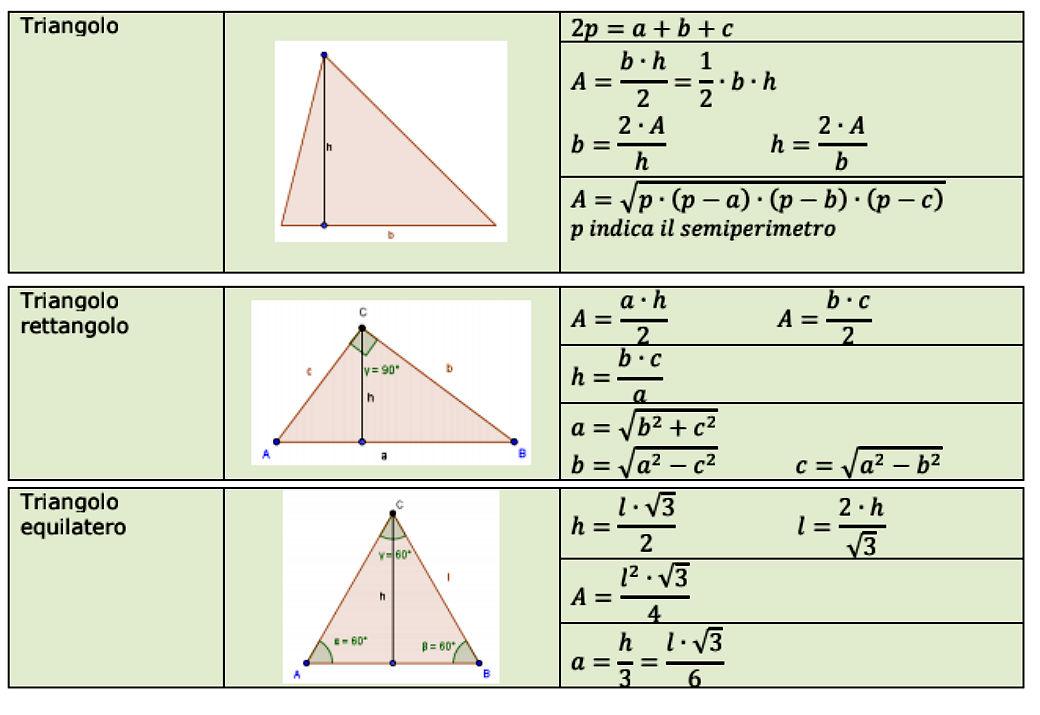
La Formula Fondamentale: Base per Altezza Diviso Due

La formula più comune e fondamentale per calcolare l'area di un triangolo è:

Area = (Base x Altezza) / 2

Ma cosa significano base e altezza? La base è uno qualsiasi dei lati del triangolo che scegliamo. L'altezza è la distanza perpendicolare (cioè, forma un angolo di 90 gradi) dalla base al vertice opposto. È come se stessimo misurando "quanto è alto" il triangolo rispetto alla base che abbiamo scelto.

Esempio pratico: Immagina un triangolo con una base di 8 cm e un'altezza di 5 cm. L'area sarebbe (8 cm x 5 cm) / 2 = 20 cm². Ricorda sempre di esprimere l'area in unità di misura al quadrato (cm², m², ecc.).

Consiglio per l'insegnante: Utilizzare materiale manipolativo come cartoncini tagliati a forma di triangolo e righelli per consentire agli studenti di misurare fisicamente la base e l'altezza. Questo approccio pratico rafforza la comprensione concettuale.

Quando l'Altezza è un Problema: La Formula di Erone

A volte, l'altezza del triangolo non è direttamente fornita. In questi casi, non disperare! Abbiamo un'arma segreta: la Formula di Erone. Questa formula è particolarmente utile quando conosciamo la lunghezza di tutti e tre i lati del triangolo.

La formula di Erone è la seguente:

Area = √[s(s - a)(s - b)(s - c)]

Dove:

• a, b, e c sono le lunghezze dei tre lati del triangolo.
• s è il semiperimetro del triangolo, calcolato come (a + b + c) / 2.

Esempio: Supponiamo di avere un triangolo con lati di 5 cm, 7 cm e 10 cm. Calcoliamo prima il semiperimetro: s = (5 + 7 + 10) / 2 = 11 cm. Ora possiamo applicare la formula di Erone: Area = √[11(11 - 5)(11 - 7)(11 - 10)] = √(11 * 6 * 4 * 1) = √264 ≈ 16.25 cm².

Consiglio per lo studente: La formula di Erone può sembrare complessa, ma è solo questione di seguir i passaggi con attenzione. Dividi il problema in parti più piccole (calcola prima il semiperimetro, poi sostituisci i valori nella formula) per semplificare il processo.

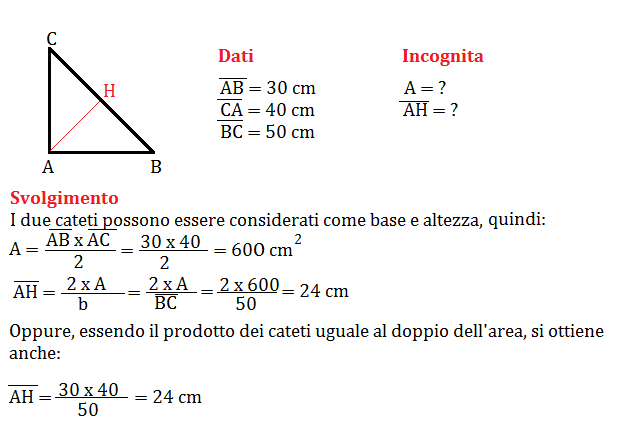
Triangoli Rettangoli: Un Caso Speciale

I triangoli rettangoli meritano un'attenzione particolare. Ricorda, un triangolo rettangolo ha un angolo di 90 gradi. I due lati che formano l'angolo retto sono chiamati cateti, e il lato opposto all'angolo retto è l'ipotenusa.

Per i triangoli rettangoli, possiamo usare una versione semplificata della formula base: uno dei cateti funge da base e l'altro cateto funge da altezza. Quindi:

Area = (Cateto 1 x Cateto 2) / 2

Questo semplifica notevolmente il calcolo dell'area, poiché non dobbiamo cercare l'altezza perpendicolare alla base.

Esempio: Un triangolo rettangolo ha cateti di 6 cm e 8 cm. L'area è (6 cm x 8 cm) / 2 = 24 cm².

Consiglio per il genitore: Aiuta tuo figlio a identificare i triangoli rettangoli negli oggetti di uso quotidiano (ad esempio, l'angolo di un libro, un tetto a falda singola). Questo li aiuterà a visualizzare e comprendere il concetto.

L'Approccio Trigonometrico: Quando Conosci Angoli e Lati

Se conosci la lunghezza di due lati del triangolo e l'angolo compreso tra essi, puoi usare una formula trigonometrica per calcolare l'area:

Area = (1/2) * a * b * sin(C)

Dove:

• a e b sono le lunghezze dei due lati.
• C è l'angolo compreso tra i lati a e b.
• sin(C) è il seno dell'angolo C. (Avrai bisogno di una calcolatrice scientifica per calcolare il seno).

Questa formula è particolarmente utile quando non è facile determinare l'altezza del triangolo. Si basa sulle proprietà trigonometriche del seno e del coseno e fornisce un modo alternativo per trovare l'area.

Esempio: Un triangolo ha lati di 10 cm e 12 cm, e l'angolo compreso tra essi è di 30 gradi. L'area è (1/2) * 10 cm * 12 cm * sin(30°) = 60 cm² * 0.5 = 30 cm² (ricorda che sin(30°) = 0.5).

Consigli Generali per il Successo

• Visualizza il problema: Disegna sempre un diagramma del triangolo. Questo ti aiuterà a identificare le informazioni fornite e a scegliere la formula appropriata.
• Verifica le unità di misura: Assicurati che tutte le lunghezze siano espresse nella stessa unità di misura (ad esempio, tutti in cm o tutti in metri).
• Esercitati, esercitati, esercitati: La pratica rende perfetti! Risolvi molti problemi diversi per familiarizzare con le diverse formule e tecniche.
• Non aver paura di chiedere aiuto: Se ti blocchi, non esitare a chiedere aiuto al tuo insegnante, tutor o compagno di studi.
• Controlla il tuo lavoro: Dopo aver calcolato l'area, ricontrolla i tuoi calcoli per assicurarti di non aver commesso errori.

L'Importanza dell'Apprendimento Concettuale

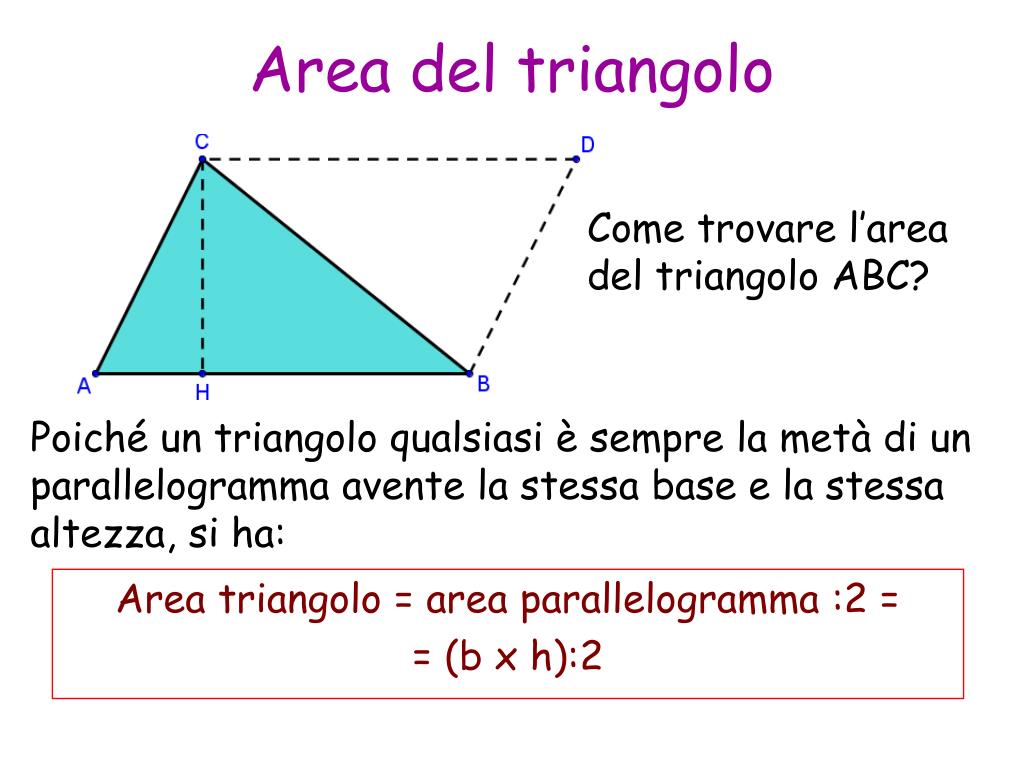
È fondamentale non limitarsi a memorizzare le formule, ma capire il perché funzionano. Ad esempio, capire che la formula (Base x Altezza) / 2 deriva dal fatto che un triangolo è esattamente metà di un parallelogramma con la stessa base e altezza. Questa comprensione concettuale ti permetterà di applicare le formule in modo più flessibile e di risolvere problemi più complessi.

Uno studio di Hiebert e Grouws (1992) ha dimostrato che gli studenti che ricevono un'istruzione incentrata sulla comprensione concettuale ottengono risultati migliori nella risoluzione dei problemi e nella capacità di trasferire le conoscenze a nuovi contesti.

Consiglio finale: Non considerare la matematica come un insieme di regole da memorizzare, ma come un linguaggio per descrivere e comprendere il mondo che ci circonda. Quando impari qualcosa di nuovo, cerca di collegarlo a ciò che già sai. Questo renderà l'apprendimento più significativo e duraturo.

Ricorda, imparare a calcolare l'area di un triangolo è solo un piccolo passo nel tuo percorso di apprendimento. Continua a esplorare, a sperimentare e a non aver paura di commettere errori. Ogni errore è un'opportunità per imparare e crescere. Abbi fiducia nelle tue capacità e vedrai che raggiungerai i tuoi obiettivi!