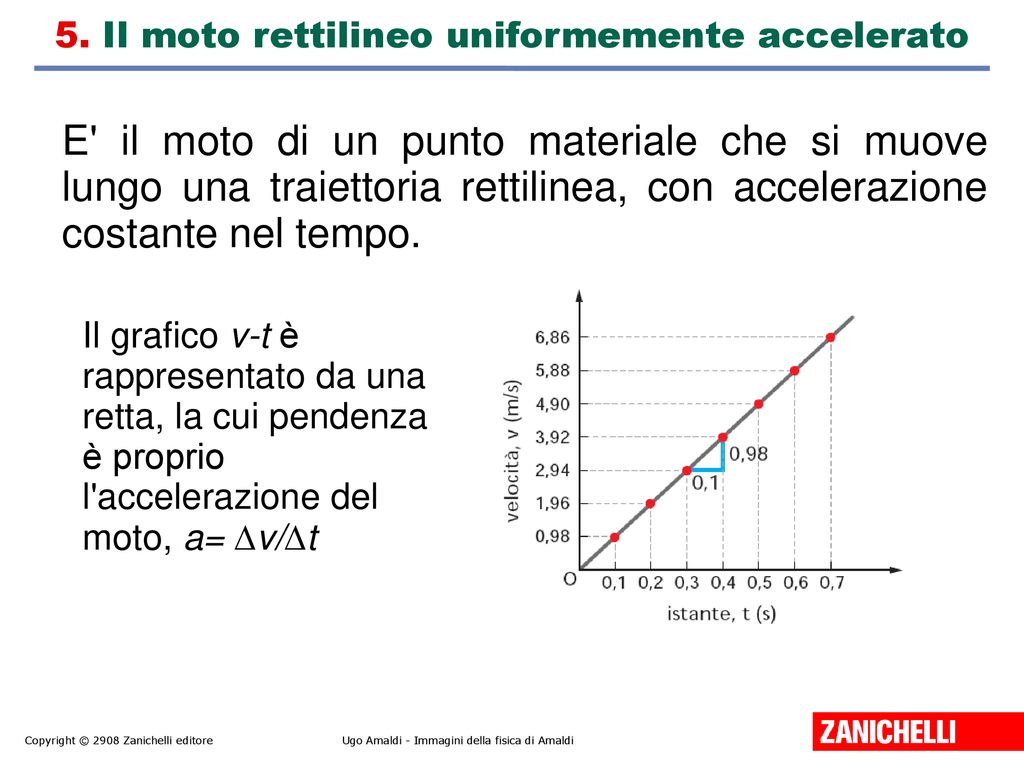
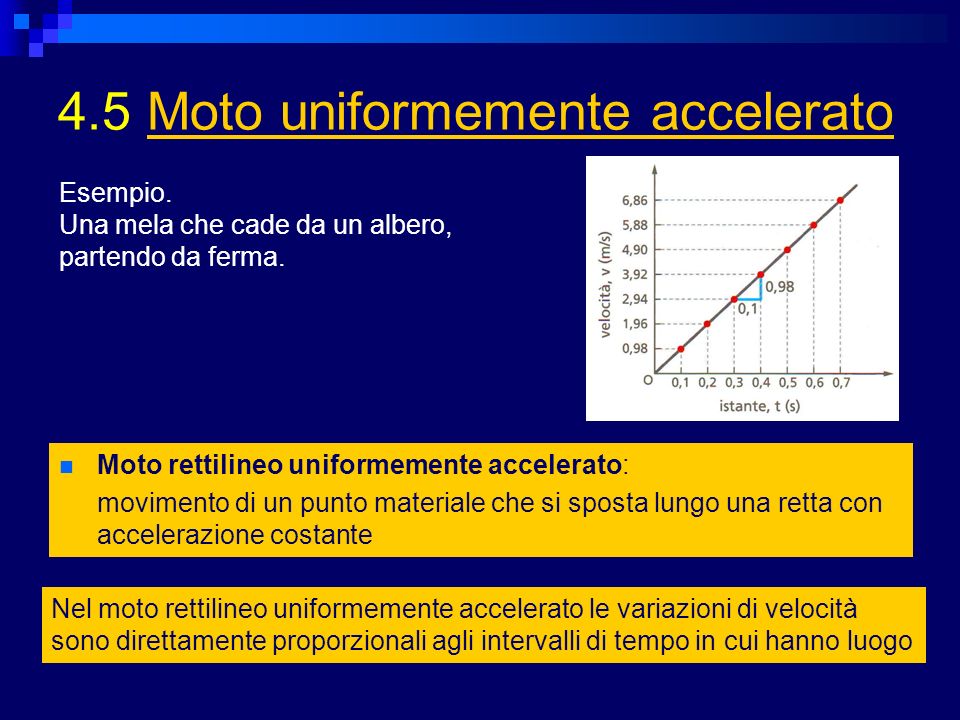
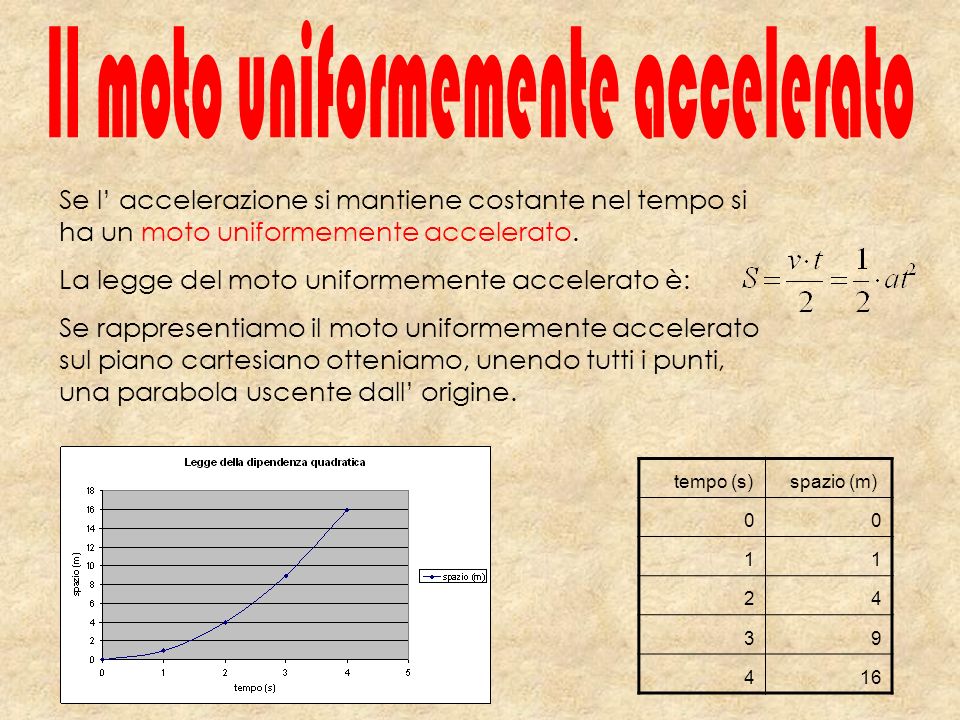
Come Trovare Il Tempo Nel Moto Uniformemente Accelerato

Il moto uniformemente accelerato (MUA) è un concetto fondamentale della fisica che descrive il movimento di un oggetto la cui velocità cambia a un tasso costante. Comprendere come calcolare il tempo in questo tipo di moto è essenziale per risolvere una vasta gamma di problemi, dalla balistica all'ingegneria civile. Questo articolo esplorerà le equazioni chiave, i concetti e le applicazioni pratiche per aiutarti a padroneggiare questo aspetto cruciale della cinematica.

Le Equazioni Fondamentali del Moto Uniformemente Accelerato

Il MUA è governato da un insieme di equazioni che mettono in relazione spazio, velocità, accelerazione e tempo. Comprendere queste equazioni è il primo passo per risolvere problemi che coinvolgono il calcolo del tempo.

Equazione 1: Velocità in Funzione del Tempo

L'equazione più fondamentale è quella che lega la velocità finale (v) alla velocità iniziale (v₀), all'accelerazione (a) e al tempo (t):

v = v₀ + a * t

Da questa equazione, possiamo ricavare il tempo:

t = (v - v₀) / a

Questa formula è utile quando conosciamo le velocità iniziale e finale e l'accelerazione.

Equazione 2: Spazio in Funzione del Tempo

Un'altra equazione importante mette in relazione lo spazio percorso (Δx) con la velocità iniziale (v₀), il tempo (t) e l'accelerazione (a):

Δx = v₀ * t + (1/2) * a * t²

Questa equazione è quadratica rispetto al tempo, quindi per trovare t, spesso è necessario risolvere un'equazione quadratica.

Equazione 3: Velocità in Funzione dello Spazio

Se non conosciamo il tempo, ma conosciamo lo spazio percorso, possiamo utilizzare l'equazione che lega la velocità finale (v), la velocità iniziale (v₀), l'accelerazione (a) e lo spazio percorso (Δx):

v² = v₀² + 2 * a * Δx

Da questa equazione, non possiamo ricavare direttamente il tempo. Tuttavia, possiamo utilizzarla per trovare la velocità finale, e poi utilizzare l'equazione 1 per trovare il tempo.

Come Risolvere Problemi che Coinvolgono il Tempo nel MUA

Risolvere problemi di MUA che richiedono il calcolo del tempo richiede un approccio sistematico.

Passo 1: Identificare le Grandezze Note e Inconosciute

Il primo passo è identificare chiaramente quali grandezze sono note (velocità iniziale, velocità finale, accelerazione, spazio percorso) e quale grandezza stiamo cercando (tempo).

Passo 2: Scegliere l'Equazione Appropriata

In base alle grandezze note, scegli l'equazione che permette di calcolare il tempo. Se conosci v, v₀ e a, usa t = (v - v₀) / a. Se conosci Δx, v₀ e a, usa Δx = v₀ * t + (1/2) * a * t² e risolvi l'equazione quadratica per t.

Passo 3: Risolvere l'Equazione

Risolvi l'equazione per il tempo. Se l'equazione è quadratica, potrebbero esserci due soluzioni. In genere, una delle due soluzioni non è fisicamente realistica (ad esempio, un tempo negativo) e può essere scartata.

Passo 4: Verificare la Soluzione

Una volta trovato il valore del tempo, è importante verificare che la soluzione sia ragionevole. Ad esempio, se stai calcolando il tempo impiegato da un'auto per accelerare da 0 a 100 km/h, la soluzione dovrebbe essere dell'ordine di pochi secondi, non di ore.

Esempi Pratici e Dati Reali

Per comprendere meglio come applicare queste equazioni, esaminiamo alcuni esempi pratici.

Esempio 1: Un'Auto in Accelerazione

Un'auto parte da ferma (v₀ = 0 m/s) e accelera uniformemente a 2 m/s² fino a raggiungere una velocità di 20 m/s. Quanto tempo impiega?

Usiamo l'equazione t = (v - v₀) / a:

t = (20 m/s - 0 m/s) / 2 m/s² = 10 s

L'auto impiega 10 secondi per raggiungere la velocità di 20 m/s.

Esempio 2: Un Oggetto in Caduta Libera

Un oggetto viene lasciato cadere da un'altezza di 50 metri. Assumendo un'accelerazione dovuta alla gravità di 9.8 m/s², quanto tempo impiega per raggiungere il suolo?

In questo caso, v₀ = 0 m/s, Δx = 50 m e a = 9.8 m/s². Usiamo l'equazione Δx = v₀ * t + (1/2) * a * t²:

50 m = 0 * t + (1/2) * 9.8 m/s² * t²

50 m = 4.9 m/s² * t²

t² = 50 m / 4.9 m/s² ≈ 10.2 s²

t ≈ √10.2 s² ≈ 3.2 s

L'oggetto impiega circa 3.2 secondi per raggiungere il suolo.

Esempio 3: Dati Reali da un Test di Accelerazione Automobilistica

Molte riviste automobilistiche eseguono test di accelerazione 0-100 km/h (circa 27.78 m/s). Consideriamo un'auto che raggiunge i 100 km/h in 5.5 secondi. Possiamo calcolare l'accelerazione media e poi usare i valori per prevedere il tempo impiegato per raggiungere velocità intermedie.

Accelerazione media: a = (27.78 m/s - 0 m/s) / 5.5 s ≈ 5.05 m/s²

Ora, quanto tempo impiegherebbe per raggiungere 50 km/h (circa 13.89 m/s)?

t = (13.89 m/s - 0 m/s) / 5.05 m/s² ≈ 2.75 s

Questi dati dimostrano come le equazioni del MUA possano essere utilizzate per analizzare e prevedere il comportamento di oggetti reali.

Considerazioni Importanti e Potenziali Errori

Quando si lavora con il moto uniformemente accelerato, è importante tenere a mente alcune considerazioni chiave per evitare errori comuni.

Unità di Misura

Assicurati che tutte le grandezze siano espresse nelle unità di misura corrette (metri per la distanza, metri al secondo per la velocità, metri al secondo quadrato per l'accelerazione, secondi per il tempo). La coerenza delle unità è fondamentale per ottenere risultati corretti.

Segno dell'Accelerazione

Presta attenzione al segno dell'accelerazione. Un'accelerazione positiva indica un aumento della velocità nella direzione positiva, mentre un'accelerazione negativa (decelerazione) indica una diminuzione della velocità o un aumento nella direzione negativa.

Equazioni Quadratiche

Quando si risolvono equazioni quadratiche, è importante considerare entrambe le soluzioni. In alcuni casi, entrambe le soluzioni possono essere fisicamente realistiche, ma in altri casi, una delle due soluzioni potrebbe essere negativa o irragionevole.

Resistenza dell'Aria

Le equazioni del MUA presuppongono che l'accelerazione sia costante. In realtà, la resistenza dell'aria può influenzare il movimento di un oggetto, soprattutto a velocità elevate. In questi casi, le equazioni del MUA forniscono solo un'approssimazione del movimento reale.

Conclusione

Calcolare il tempo nel moto uniformemente accelerato è una competenza essenziale per chiunque studi fisica o ingegneria. Comprendere le equazioni fondamentali, identificare le grandezze note e sconosciute, scegliere l'equazione appropriata e risolvere l'equazione con attenzione sono i passi chiave per risolvere questi problemi con successo. Ricorda di prestare attenzione alle unità di misura, al segno dell'accelerazione e alle limitazioni del modello (come la resistenza dell'aria).

Metti in pratica queste conoscenze risolvendo una varietà di esercizi e problemi. Più ti eserciti, più diventerai abile nel padroneggiare il calcolo del tempo nel moto uniformemente accelerato. Non aver paura di sperimentare e di affrontare problemi sempre più complessi. La comprensione approfondita di questi concetti ti aprirà le porte a una comprensione più completa del mondo che ti circonda!