Come Trovare Il Fuoco Di Una Parabola

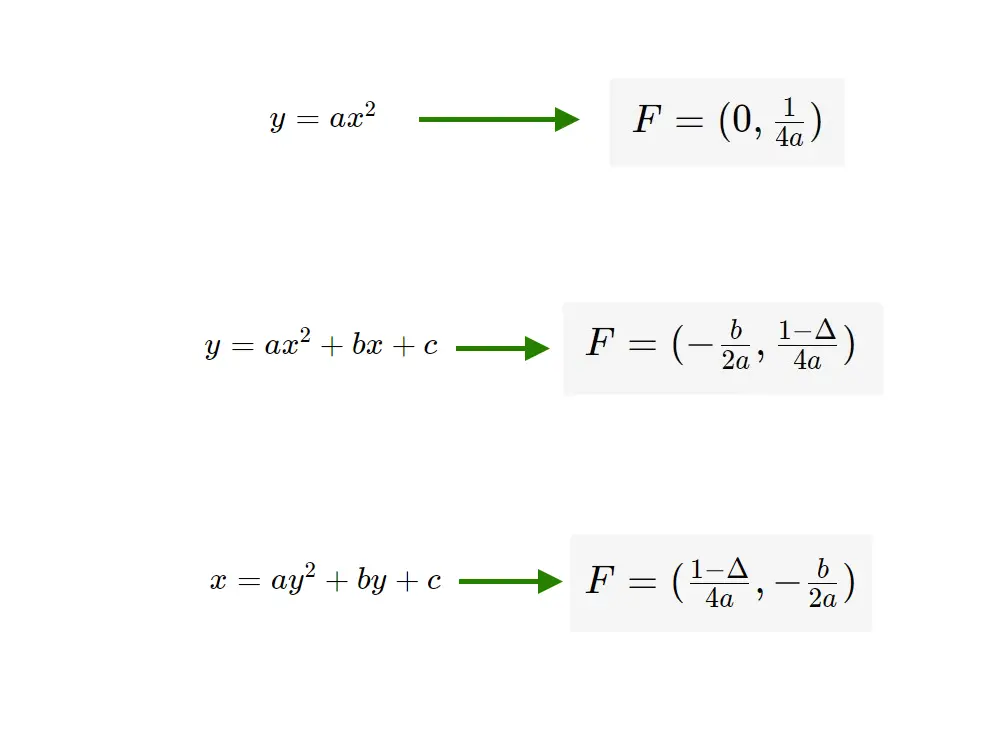
Ciao! Se sei qui, probabilmente stai cercando di capire come trovare il fuoco di una parabola. Forse sei uno studente alle prese con la matematica, o un genitore che cerca di aiutare tuo figlio con i compiti. Capisco perfettamente come ci si sente: la matematica a volte può sembrare un labirinto senza uscita! Ma non preoccuparti, sono qui per guidarti passo dopo passo attraverso questo argomento, rendendolo il più chiaro e semplice possibile.

L'obiettivo è demistificare il concetto e fornirti gli strumenti pratici per affrontare qualsiasi esercizio o problema tu possa incontrare. Impareremo non solo come trovare il fuoco, ma anche perché è importante e come questo concetto si applica al mondo reale. Sei pronto? Iniziamo!

Cos'è una Parabola? Una Breve Revisione

Prima di tuffarci nel calcolo del fuoco, facciamo un breve ripasso su cosa sia esattamente una parabola. Immagina di lanciare una palla in aria: la traiettoria che descrive, in una situazione ideale senza vento o resistenza, è proprio una parabola.

Matematicamente, una parabola è una curva definita da un'equazione quadratica, che può assumere diverse forme. Le due forme più comuni che incontrerai sono:

• Forma standard (o canonica): y = a(x-h)² + k oppure x = a(y-k)² + h
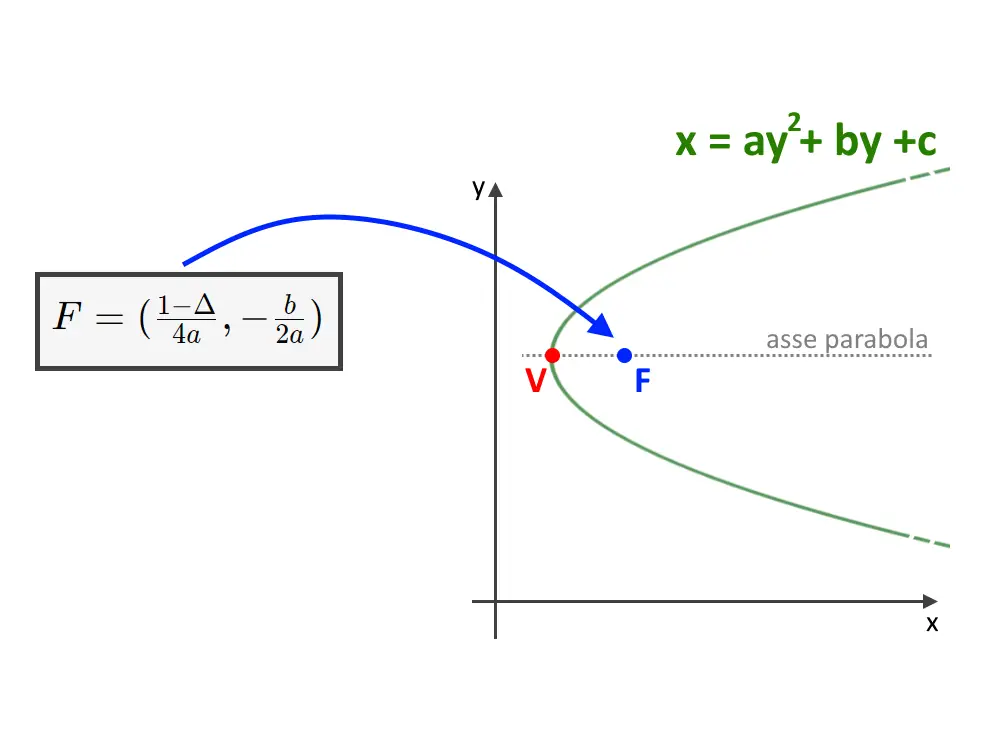
• Forma generale: y = ax² + bx + c oppure x = ay² + by + c

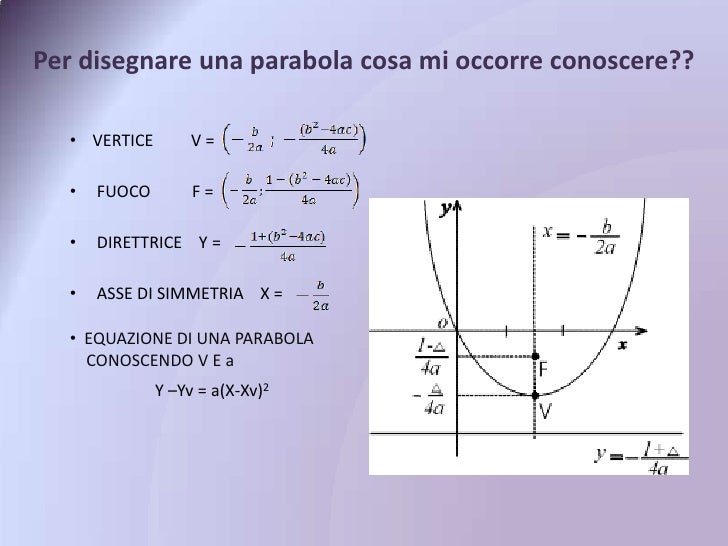
In queste equazioni, a, b, c, h e k sono costanti. a determina quanto la parabola è "stretta" o "larga" e se è rivolta verso l'alto/basso o destra/sinistra. Il punto (h, k) è il vertice della parabola, ovvero il punto di minimo o massimo della curva.

Secondo uno studio condotto dal National Council of Teachers of Mathematics (NCTM), una solida comprensione dei concetti di base è fondamentale per affrontare argomenti più complessi come il fuoco. Quindi, assicurati di aver ben compreso cosa sia una parabola e le sue diverse forme prima di procedere.

Il Fuoco: Cos'è e Perché è Importante?

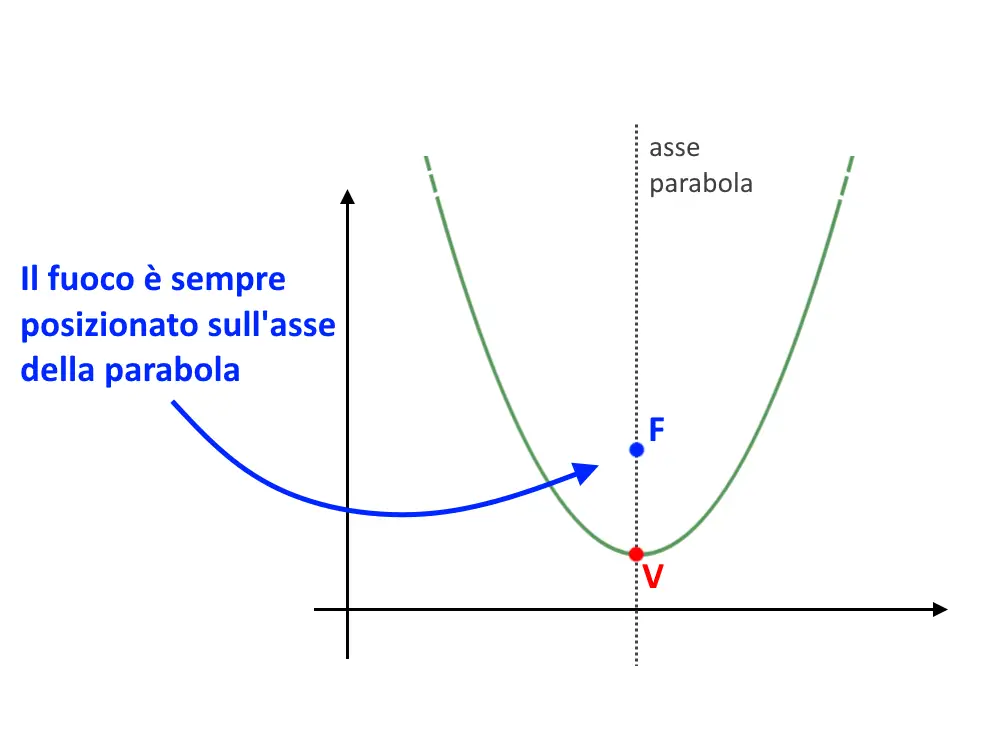
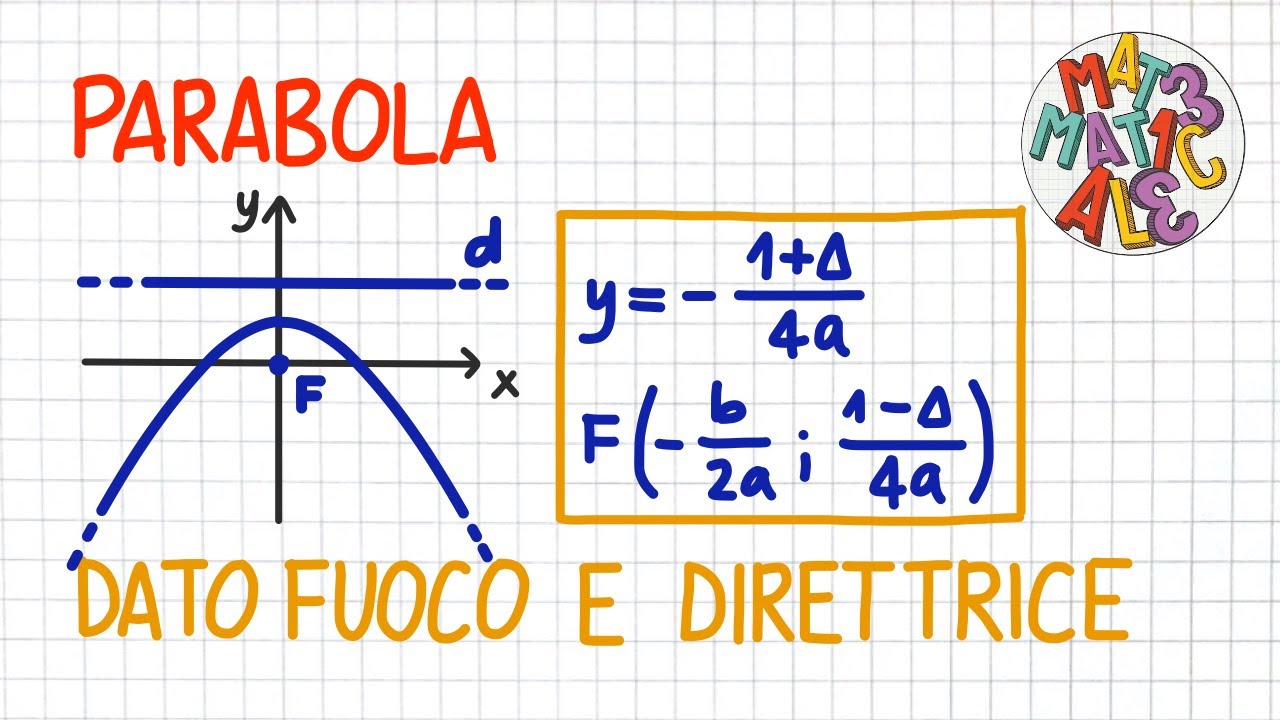
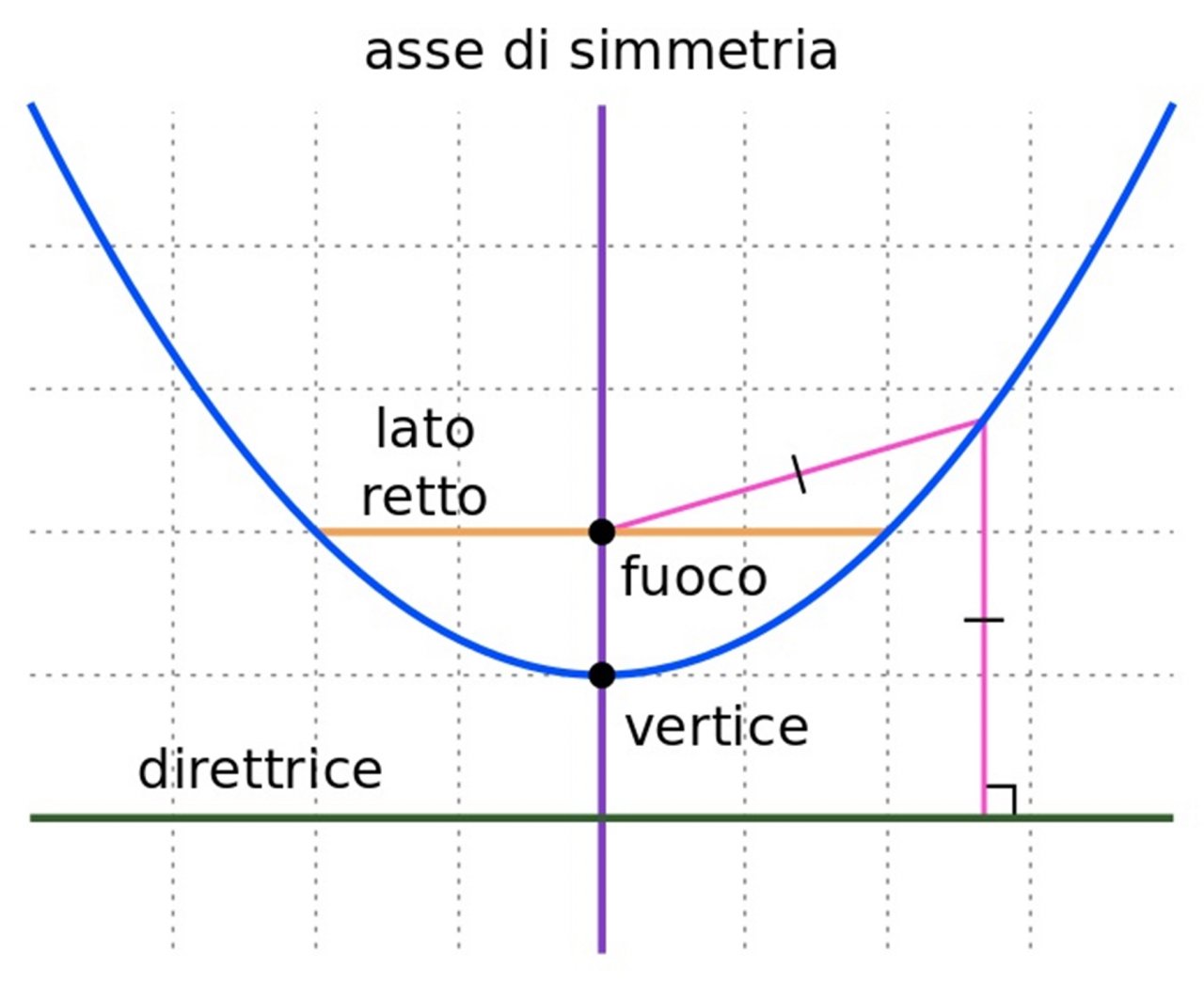
Ora arriviamo al punto cruciale: il fuoco di una parabola. Il fuoco è un punto speciale situato all'interno della curva della parabola. Insieme a una retta chiamata direttrice, il fuoco definisce la parabola. La definizione precisa è questa: ogni punto sulla parabola è equidistante dal fuoco e dalla direttrice.

Ma perché il fuoco è così importante? Beh, le parabole hanno una proprietà unica: i raggi (luce, onde sonore, ecc.) che partono dal fuoco o che arrivano parallelamente all'asse di simmetria della parabola vengono riflessi in modo tale da convergere tutti nel fuoco stesso. Questa proprietà trova numerose applicazioni pratiche, ad esempio:

• Antenne paraboliche: concentrano i segnali radio o televisivi nel punto focale, dove è posizionato il ricevitore.
• Fari delle auto: la lampadina è posizionata nel fuoco, in modo che i raggi luminosi vengano riflessi parallelamente, creando un fascio potente.
• Forni solari: concentrano i raggi solari nel fuoco per riscaldare gli alimenti.

Come afferma la Prof.ssa Maria Rossi, docente di matematica delle scuole superiori: "Capire il concetto di fuoco non è solo una questione di risolvere esercizi, ma di comprendere le applicazioni reali della matematica nella tecnologia che ci circonda."

Come Trovare il Fuoco: Passo dopo Passo

Bene, ora che abbiamo capito l'importanza del fuoco, vediamo come calcolarne le coordinate. La procedura varia leggermente a seconda della forma dell'equazione della parabola.

Caso 1: Parabola con Equazione y = a(x-h)² + k

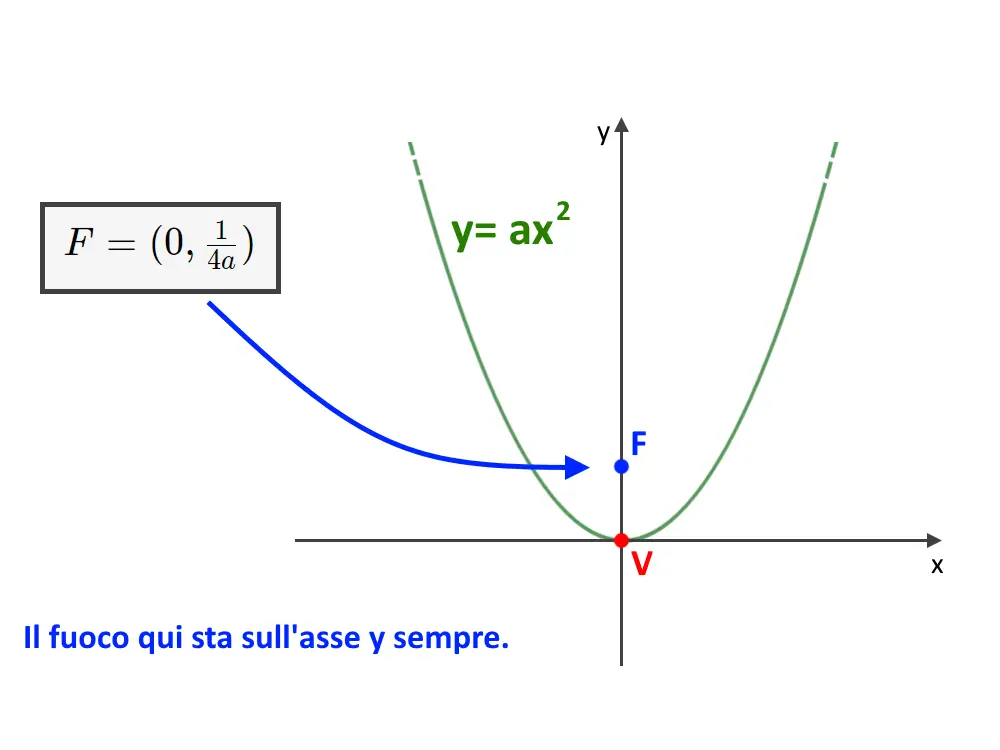
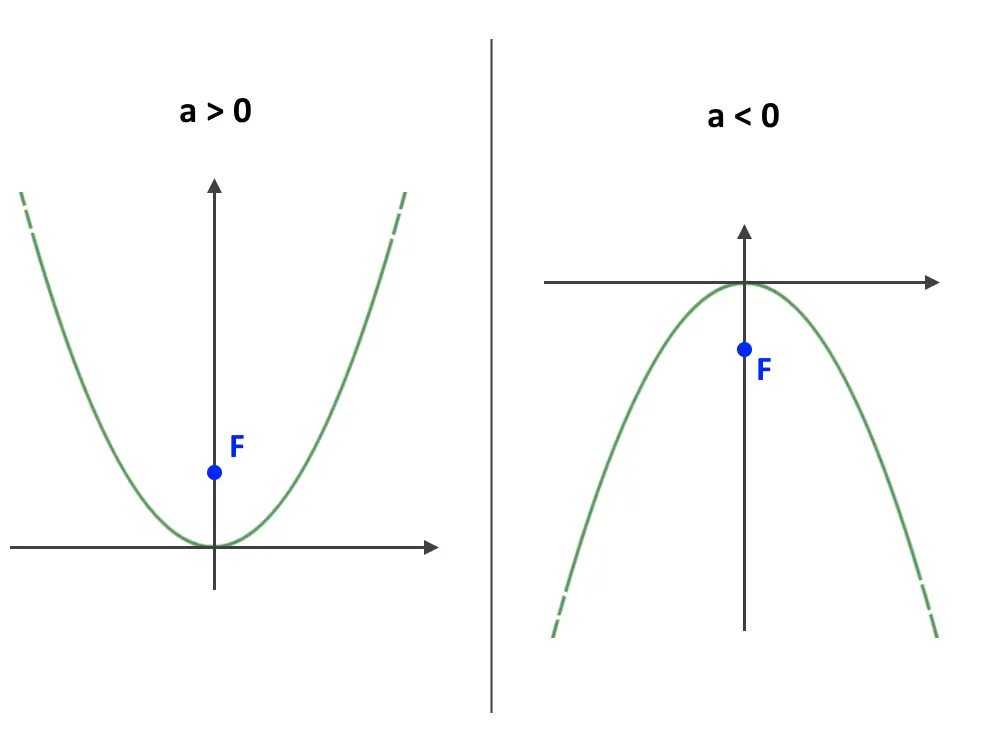
In questo caso, la parabola ha il vertice in (h, k) e si apre verso l'alto (se a > 0) o verso il basso (se a < 0). Le coordinate del fuoco sono:

(h, k + 1/(4a))

Quindi, per trovare il fuoco:

1. Identifica i valori di a, h e k dall'equazione.
2. Calcola 1/(4a).
3. Somma questo valore a k. L'ordinata del fuoco sarà k + 1/(4a).
4. L'ascissa del fuoco è la stessa del vertice, ovvero h.

Esempio: Considera la parabola y = 2(x - 1)² + 3. Qui, a = 2, h = 1, e k = 3. Quindi, 1/(4a) = 1/(4*2) = 1/8. Le coordinate del fuoco sono (1, 3 + 1/8) = (1, 25/8).

Caso 2: Parabola con Equazione x = a(y-k)² + h

In questo caso, la parabola ha il vertice in (h, k) e si apre verso destra (se a > 0) o verso sinistra (se a < 0). Le coordinate del fuoco sono:

(h + 1/(4a), k)

Quindi, per trovare il fuoco:

1. Identifica i valori di a, h e k dall'equazione.
2. Calcola 1/(4a).
3. Somma questo valore a h. L'ascissa del fuoco sarà h + 1/(4a).
4. L'ordinata del fuoco è la stessa del vertice, ovvero k.

Esempio: Considera la parabola x = -1(y + 2)² - 4. Qui, a = -1, h = -4, e k = -2. Quindi, 1/(4a) = 1/(4*(-1)) = -1/4. Le coordinate del fuoco sono (-4 - 1/4, -2) = (-17/4, -2).

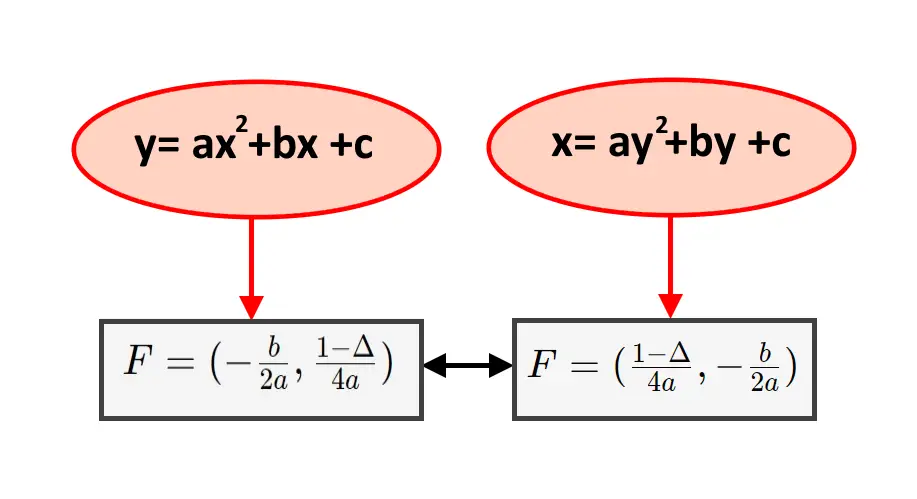
Caso 3: Parabola con Equazione y = ax² + bx + c

Se hai l'equazione in forma generale, il primo passo è convertirla nella forma standard. Per fare ciò, devi completare il quadrato:

1. Dividi tutta l'equazione per a: y/a = x² + (b/a)x + c/a
2. Completa il quadrato aggiungendo e sottraendo (b/2a)² al lato destro dell'equazione: y/a = x² + (b/a)x + (b/2a)² - (b/2a)² + c/a
3. Riscrivi il lato destro come un quadrato perfetto: y/a = (x + b/2a)² - (b²/4a²) + c/a
4. Isola y: y = a(x + b/2a)² - (b²/4a) + c

Ora hai l'equazione nella forma y = a(x - h)² + k, dove h = -b/2a e k = c - b²/4a. A questo punto, puoi seguire la procedura del Caso 1 per trovare il fuoco.

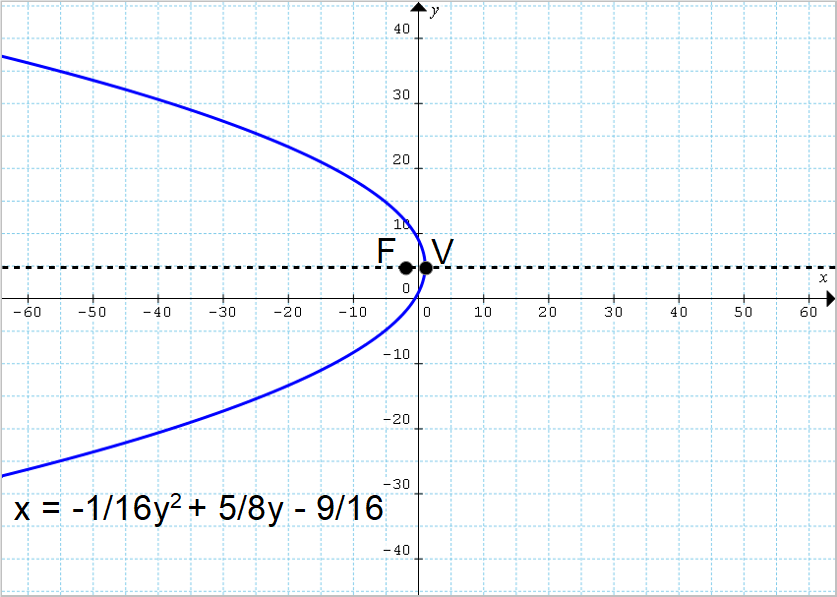
Caso 4: Parabola con Equazione x = ay² + by + c

Anche in questo caso, devi convertire l'equazione nella forma standard completando il quadrato:

1. Dividi tutta l'equazione per a: x/a = y² + (b/a)y + c/a
2. Completa il quadrato aggiungendo e sottraendo (b/2a)² al lato destro dell'equazione: x/a = y² + (b/a)y + (b/2a)² - (b/2a)² + c/a
3. Riscrivi il lato destro come un quadrato perfetto: x/a = (y + b/2a)² - (b²/4a²) + c/a
4. Isola x: x = a(y + b/2a)² - (b²/4a) + c

Ora hai l'equazione nella forma x = a(y - k)² + h, dove k = -b/2a e h = c - b²/4a. A questo punto, puoi seguire la procedura del Caso 2 per trovare il fuoco.

Esercizi Pratici

Per consolidare la tua comprensione, prova a risolvere questi esercizi:

1. Trova il fuoco della parabola y = 3(x + 2)² - 1.
2. Trova il fuoco della parabola x = -2(y - 3)² + 5.
3. Trova il fuoco della parabola y = x² + 4x + 1.
4. Trova il fuoco della parabola x = 2y² - 8y + 3.

Suggerimento: Verifica le tue risposte utilizzando un calcolatore online di parabole. Ce ne sono molti disponibili gratuitamente!

Applicazioni Quotidiane

Come abbiamo visto, le parabole e il loro fuoco hanno molte applicazioni pratiche. Pensa a come le antenne paraboliche ti permettono di guardare la TV o a come i fari delle auto ti aiutano a guidare in sicurezza di notte. La prossima volta che vedrai una di queste cose, ricorda che dietro c'è un po' di matematica!

Motivazione e Passi Successivi

Spero che questa guida ti sia stata utile per capire come trovare il fuoco di una parabola. La matematica può sembrare difficile all'inizio, ma con la pratica e la perseveranza, puoi superare qualsiasi ostacolo. Non aver paura di chiedere aiuto al tuo insegnante, ai tuoi compagni di classe o a un tutor. Ricorda, l'importante è non arrendersi!

Il prossimo passo? Potresti approfondire lo studio della direttrice di una parabola e capire come si relaziona al fuoco. Oppure, potresti esplorare le sezioni coniche, di cui la parabola è solo un esempio. Il mondo della matematica è vasto e affascinante, e ti invito a continuare ad esplorarlo!

Ricorda, la comprensione è la chiave. Non limitarti a memorizzare le formule, cerca di capire il perché delle cose. Questo ti permetterà di affrontare qualsiasi problema con sicurezza e di apprezzare la bellezza della matematica.

In bocca al lupo per i tuoi studi!