Come Si Trova L'area Del Triangolo

Ciao! Capisco perfettamente. La geometria, e in particolare l'area dei triangoli, può sembrare complicata all'inizio. Molti studenti si sentono persi tra formule e concetti astratti. Non preoccuparti, non sei solo! L'obiettivo di questo articolo è quello di rendere il calcolo dell'area del triangolo semplice, chiaro e persino divertente. Insieme, supereremo le difficoltà e scopriremo come affrontare questi problemi con fiducia.

Comprendere il Concetto di Area

Prima di tuffarci nelle formule, cerchiamo di capire cos'è l'area. Pensa all'area come alla quantità di spazio bidimensionale che una figura occupa. Immagina di dover dipingere un triangolo su un muro: l'area ti dice quanta pittura ti serve. L'unità di misura dell'area è sempre al quadrato, come centimetri quadrati (cm²) o metri quadrati (m²).

Per visualizzare meglio, immagina di riempire il triangolo con tanti piccoli quadratini di 1 cm di lato ciascuno. Contare quanti quadratini ci stanno dentro ti darà una stima dell'area. Questo approccio pratico aiuta a rendere il concetto più tangibile, soprattutto per chi apprende in modo visivo o cinestesico (Sousa, 2017, "How the Brain Learns").

La Formula Fondamentale: Base per Altezza Diviso Due

La formula più comune per calcolare l'area di un triangolo è:

Area = (base × altezza) / 2

Ma cosa significano base e altezza?

Definizione di Base e Altezza

La base è uno qualsiasi dei lati del triangolo. Non importa quale scegli come base. L'altezza, invece, è la distanza perpendicolare (cioè, che forma un angolo di 90 gradi) dalla base al vertice opposto. Pensa all'altezza come ad una linea retta che cade verticalmente dalla punta del triangolo alla base.

Un errore comune è confondere l'altezza con un lato obliquo del triangolo. L'altezza deve essere sempre perpendicolare alla base. In un triangolo rettangolo, uno dei lati (che forma l'angolo retto) può fungere da altezza se l'altro lato è considerato la base. Questo rende il calcolo particolarmente semplice in questi casi.

Esempio Pratico

Immagina un triangolo con una base di 8 cm e un'altezza di 5 cm. Per trovare l'area, seguiamo questi passaggi:

1. Moltiplica la base per l'altezza: 8 cm × 5 cm = 40 cm²
2. Dividi il risultato per 2: 40 cm² / 2 = 20 cm²

Quindi, l'area del triangolo è di 20 cm².

Consiglio per gli insegnanti: Utilizzare oggetti reali, come cartoncini a forma di triangolo, per far sperimentare agli studenti la misurazione della base e dell'altezza. Questo approccio pratico rafforza la comprensione del concetto (Wieman, 2014, "Improving How Universities Teach Science").

Quando l'Altezza è Esterna al Triangolo

Nei triangoli ottusangoli (quelli con un angolo maggiore di 90 gradi), l'altezza può trovarsi all'esterno del triangolo. In questo caso, devi prolungare la base per poter tracciare una linea perpendicolare dal vertice opposto alla base estesa. Non farti spaventare da questa situazione! Il principio rimane lo stesso: l'altezza è sempre la distanza perpendicolare dalla base (o dal suo prolungamento) al vertice opposto.

Consiglio per gli studenti: Disegna sempre il triangolo chiaramente e individua la base e il vertice opposto. Utilizza un righello e una squadra per tracciare l'altezza in modo preciso. La precisione nel disegno aiuta a visualizzare correttamente il problema.

La Formula di Erone: Quando Conosci i Lati

Se non conosci l'altezza, ma conosci la lunghezza di tutti e tre i lati del triangolo (chiamiamoli a, b, e c), puoi usare la formula di Erone:

Area = √[s(s - a)(s - b)(s - c)]

Dove s è il semiperimetro del triangolo, calcolato come:

s = (a + b + c) / 2

Questa formula può sembrare complicata, ma è molto utile quando non puoi misurare direttamente l'altezza. Richiede un po' di calcolo, ma con la pratica diventerà più semplice.

Esempio Pratico con la Formula di Erone

Immagina un triangolo con lati di lunghezza a = 5 cm, b = 7 cm e c = 8 cm. Calcoliamo l'area usando la formula di Erone:

1. Calcola il semiperimetro: s = (5 + 7 + 8) / 2 = 10 cm
2. Applica la formula di Erone: Area = √[10(10 - 5)(10 - 7)(10 - 8)] = √(10 × 5 × 3 × 2) = √300 ≈ 17.32 cm²

Quindi, l'area del triangolo è approssimativamente 17.32 cm².

Triangoli Speciali: Semplificazioni e Scorciatoie

Alcuni tipi di triangoli offrono scorciatoie per il calcolo dell'area:

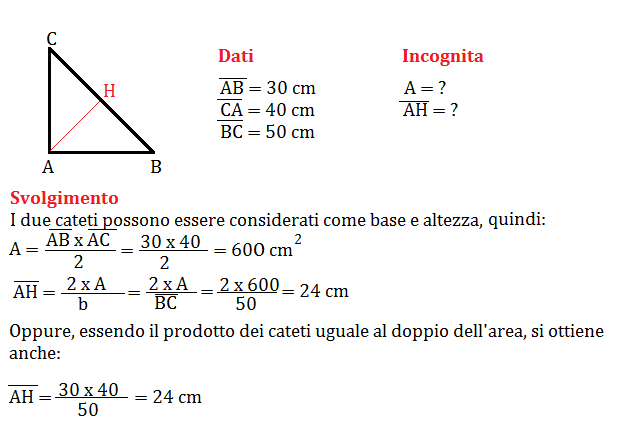
• Triangolo Rettangolo: Come accennato, l'area è semplicemente (cateto1 × cateto2) / 2. Non è necessario calcolare l'altezza separatamente.
• Triangolo Equilatero: Un triangolo equilatero ha tutti i lati uguali. Se conosci la lunghezza di un lato (l), puoi usare la formula: Area = (√3 / 4) × l².

Riconoscere questi triangoli speciali può farti risparmiare tempo e fatica!

Errori Comuni da Evitare

Ecco alcuni errori comuni che gli studenti commettono quando calcolano l'area dei triangoli:

• Confondere l'altezza con un lato obliquo. Ricorda, l'altezza deve essere perpendicolare alla base.
• Dimenticare di dividere per 2. La formula è (base × altezza) diviso 2.
• Usare unità di misura errate. Assicurati che tutte le misure siano nella stessa unità (ad esempio, tutti centimetri) prima di calcolare l'area. Il risultato sarà quindi in unità quadrate (ad esempio, cm²).
• Applicare la formula di Erone senza calcolare correttamente il semiperimetro. Assicurati di aver calcolato correttamente il valore di s.

Prestando attenzione a questi errori, puoi evitare di commettere errori costosi.

Consigli Pratici per Apprendere e Insegnare

Ecco alcuni consigli pratici per studenti, insegnanti e genitori:

• Per gli studenti:
  • Fai molti esercizi! La pratica rende perfetti.
  • Disegna sempre un diagramma chiaro del problema.
  • Verifica sempre la tua risposta per assicurarti che sia ragionevole.
  • Non aver paura di chiedere aiuto! Se ti blocchi, chiedi al tuo insegnante, a un compagno di classe o a un tutor.
• Per gli insegnanti:
  • Utilizza approcci didattici diversi per soddisfare i diversi stili di apprendimento.
  • Utilizza oggetti reali e manipolativi per rendere i concetti più tangibili.
  • Offri agli studenti molte opportunità di praticare e ricevere feedback.
  • Incoraggia la collaborazione e la discussione tra gli studenti.
• Per i genitori:
  • Incoraggia tuo figlio a fare i compiti e a studiare regolarmente.
  • Offri aiuto se tuo figlio ha difficoltà, o cerca un tutor.
  • Crea un ambiente di apprendimento positivo e di supporto.
  • Festeggia i successi di tuo figlio!

Consiglio extra: Esistono molte risorse online, come video tutorial e esercizi interattivi, che possono aiutarti a imparare e praticare il calcolo dell'area dei triangoli. Sfrutta al meglio queste risorse!

Conclusione: Sei Più Capace di Quanto Pensi!

Spero che questo articolo ti abbia fornito una comprensione più chiara e completa di come calcolare l'area dei triangoli. Ricorda, la matematica è come un gioco: più giochi, più diventi bravo. Non arrenderti di fronte alle difficoltà, e continua a esercitarti. Con un po' di impegno e la giusta strategia, puoi superare qualsiasi sfida. Credi in te stesso e nelle tue capacità! In bocca al lupo!