Come Si Trova L'area Del Pentagono
Ciao amici studenti! Immaginate di avere tra le mani una sfida, un piccolo enigma geometrico a forma di pentagono. Non temete, perché insieme, passo dopo passo, scopriremo come misurare la sua area. Non si tratta solo di numeri e formule; è un viaggio nella bellezza della matematica, un'avventura che ci insegna a crescere e a non arrenderci di fronte alle difficoltà.
Il Pentagono Regolare: Un Primo Approccio
Iniziamo con un pentagono regolare, una figura elegante dove tutti i lati e gli angoli sono uguali. La sua simmetria ci offre un punto di partenza favorevole. Immaginate di dividere questo pentagono in cinque triangoli identici, tutti con un vertice al centro della figura. Ogni triangolo è isoscele, con due lati uguali che coincidono con il raggio del pentagono circoscritto.
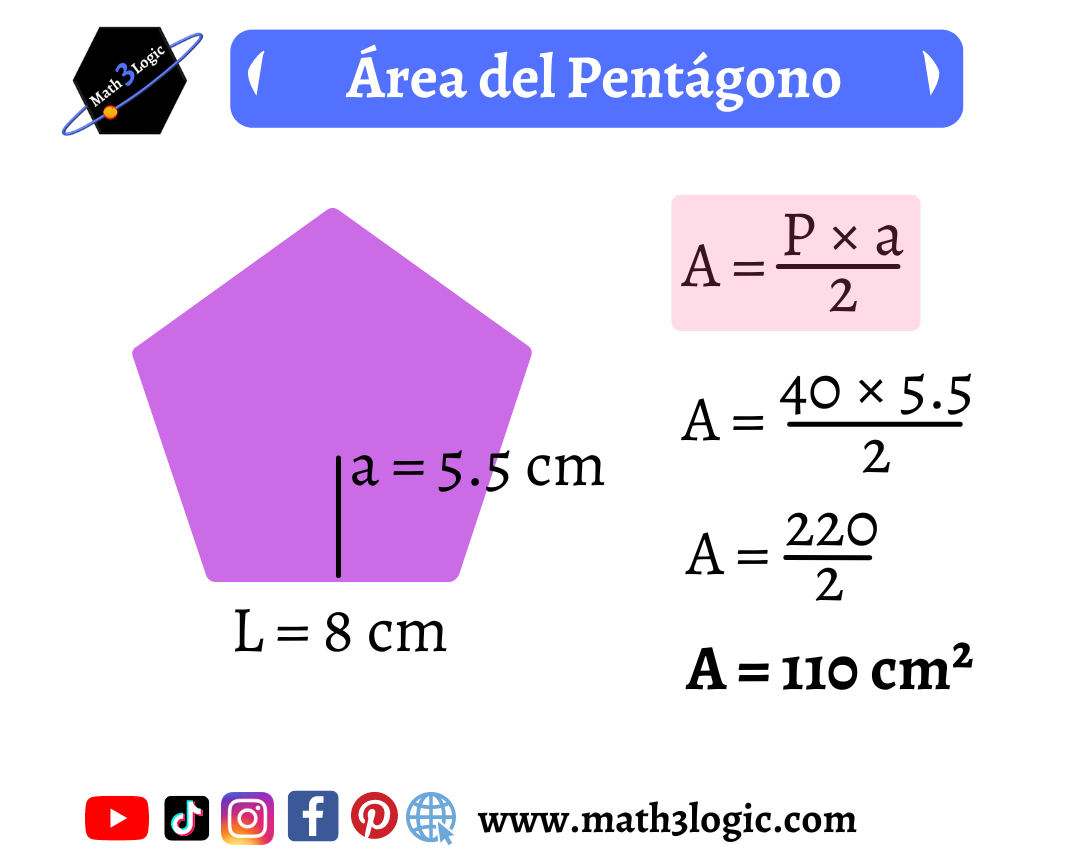
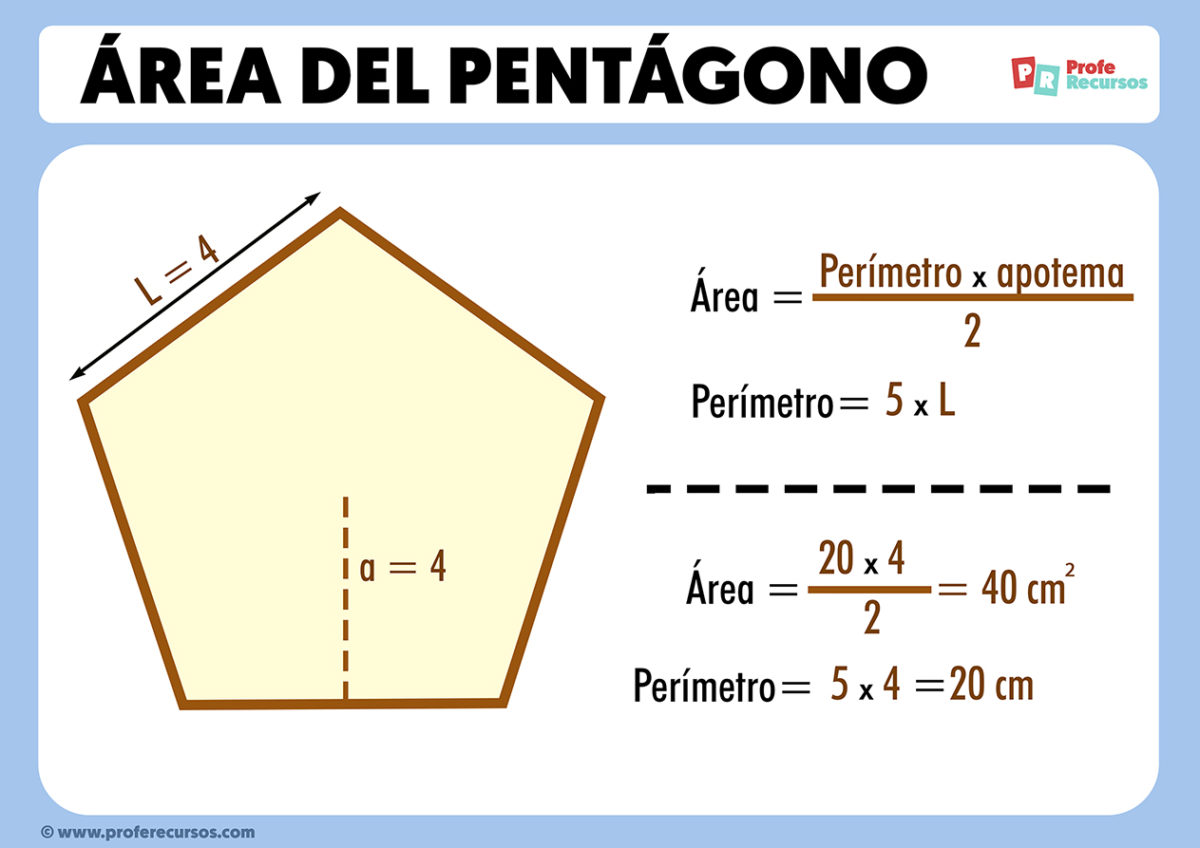
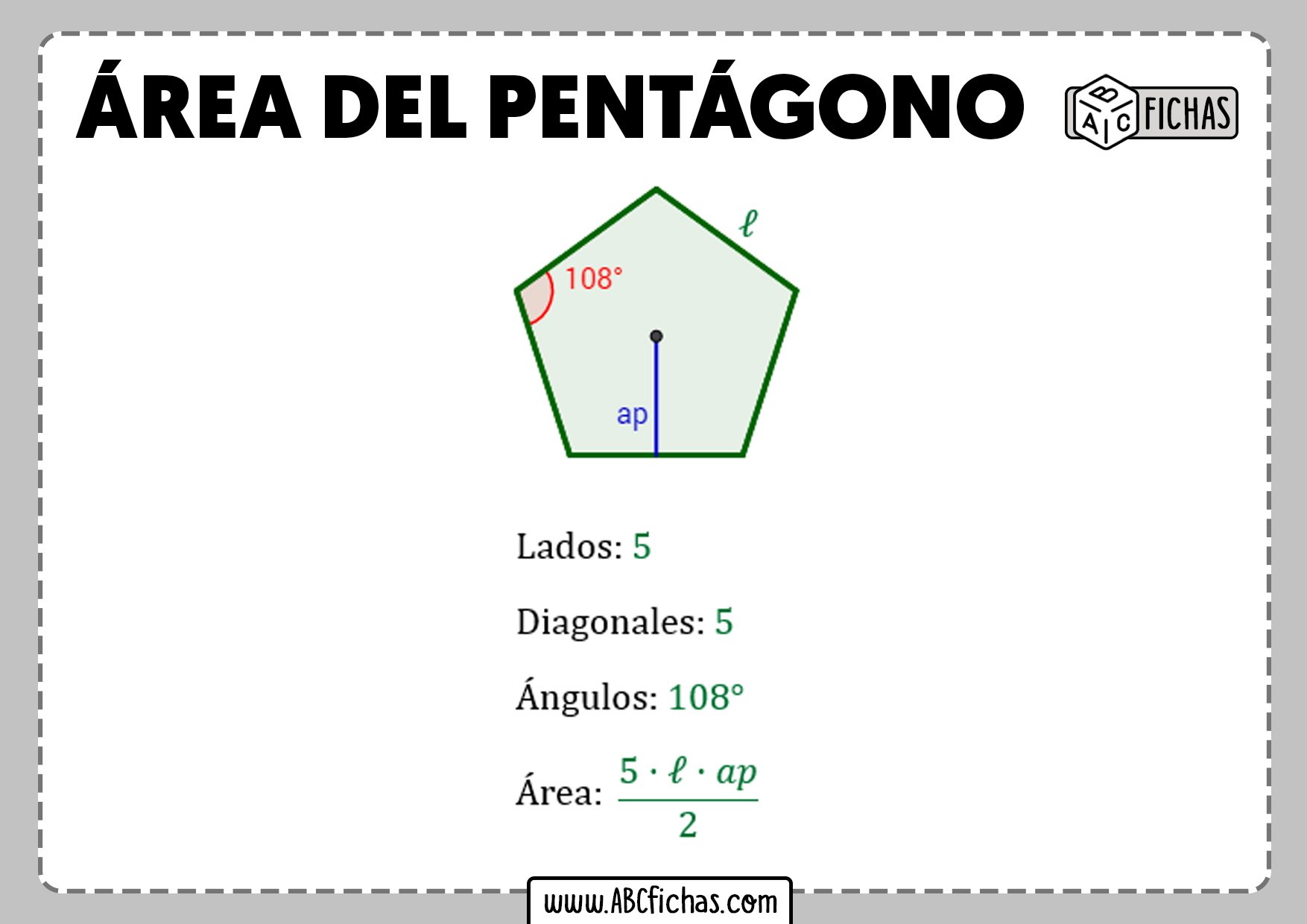
Ora, concentriamoci su uno di questi triangoli. Per calcolare la sua area, abbiamo bisogno della base (che è un lato del pentagono) e dell'altezza (l'apotema del pentagono). L'apotema è la distanza dal centro del pentagono al punto medio di un lato. Se conosciamo la lunghezza del lato (l) e l'apotema (a), l'area di un triangolo è (1/2) * l * a.
Poiché abbiamo cinque triangoli identici, l'area del pentagono regolare è semplicemente cinque volte l'area di un triangolo: Area = 5 * (1/2) * l * a, che può essere semplificata come Area = (5/2) * l * a. Memorizzate questa formula, è un tesoro!
Cosa succede se non conosciamo l'apotema?
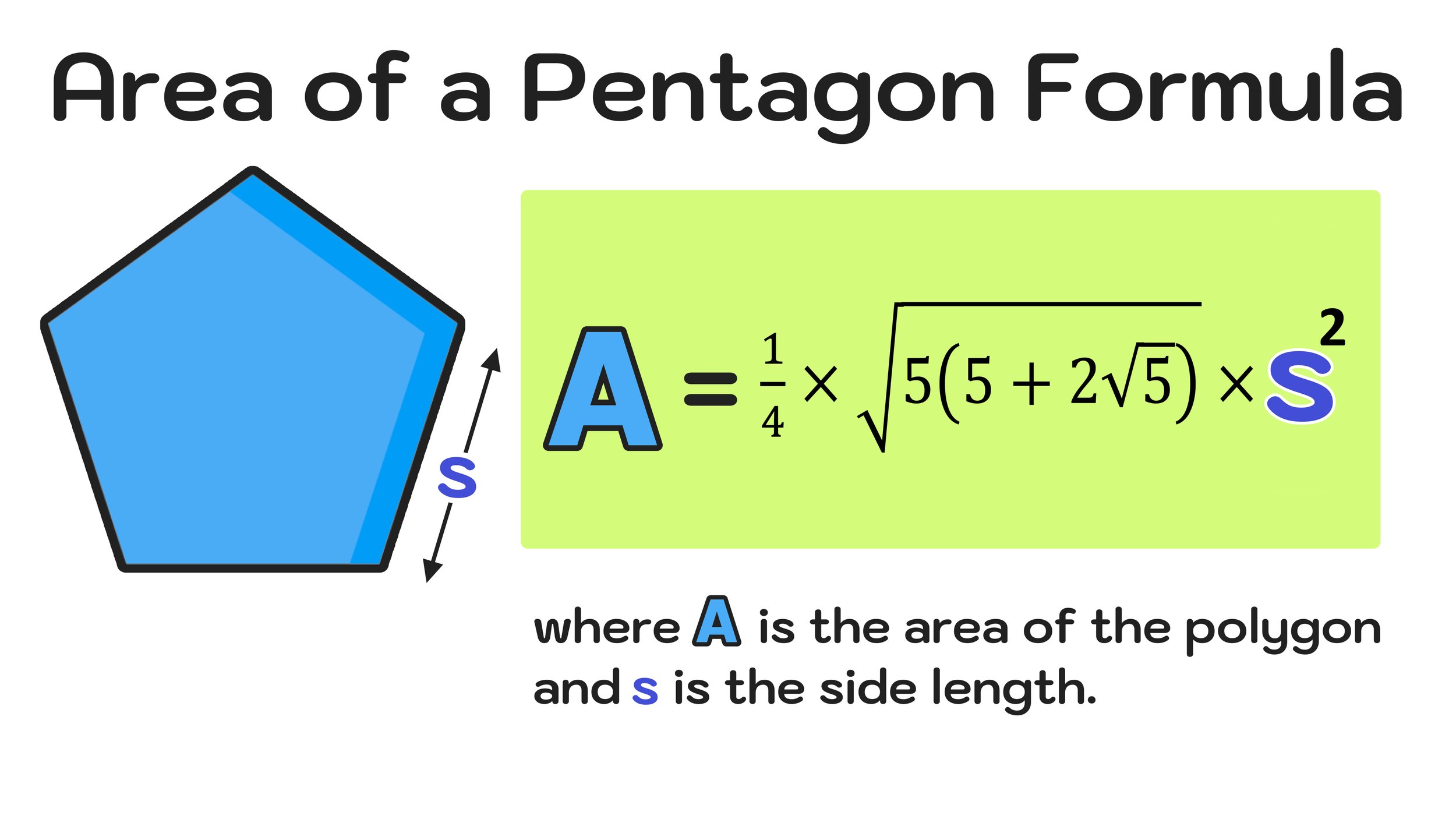
Non disperate! La trigonometria è nostra amica. L'apotema può essere calcolata se conosciamo la lunghezza del lato e l'angolo al centro di uno dei triangoli. Questo angolo è 360°/5 = 72°. Dividendo il triangolo isoscele in due triangoli rettangoli, possiamo usare la tangente dell'angolo di 36° (metà di 72°) per trovare la relazione tra metà del lato e l'apotema. L'apotema sarà quindi uguale a (l/2) / tan(36°). Ricordate, la perseveranza è la chiave!
Il Pentagono Irregolare: Una Sfida Diversa
Cosa fare, invece, se il pentagono non è regolare? La situazione si fa un po' più complessa, ma non impossibile. Invece di cercare una formula magica, dobbiamo usare un approccio più creativo. Possiamo dividere il pentagono irregolare in triangoli e quadrilateri più piccoli, figure di cui sappiamo calcolare l'area. Ad esempio, possiamo tracciare diagonali all'interno del pentagono per creare tre triangoli. Calcoliamo l'area di ciascun triangolo e sommiamo i risultati. La curiosità è il motore che ci spinge a trovare nuove soluzioni.
Oppure, possiamo utilizzare il metodo delle coordinate. Se conosciamo le coordinate dei cinque vertici del pentagono in un piano cartesiano, possiamo usare una formula che coinvolge i determinanti di matrici per calcolare l'area. Questo metodo richiede un po' di algebra lineare, ma è un potente strumento a nostra disposizione.
Riflessioni Finali
Calcolare l'area di un pentagono non è solo un esercizio di matematica; è un'esperienza che ci insegna a pensare in modo critico, a scomporre problemi complessi in parti più semplici e a non aver paura di sperimentare. La prossima volta che vi troverete di fronte a una sfida, ricordatevi del pentagono: dividetelo in parti più gestibili, cercate gli strumenti giusti e non arrendetevi finché non avrete trovato la soluzione. E ricordatevi sempre di abbracciare l'umiltà, riconoscendo che c'è sempre qualcosa di nuovo da imparare.
Buon studio e buona esplorazione geometrica!
![Come Si Trova L'area Del Pentagono Cómo sacar el ÁREA de un PENTÁGONO - [resumen fácil + EJERCICIOS]](https://cdn0.unprofesor.com/es/posts/2/1/9/como_sacar_el_area_de_un_pentagono_4912_orig.jpg)