Come Si Trova L Altezza Relativa All Ipotenusa

Ciao a tutti, amici studenti! Oggi esploreremo un piccolo tesoro della geometria: come trovare l'altezza relativa all'ipotenusa in un triangolo rettangolo. Potrebbe sembrare una sfida matematica, ma in realtà è un'opportunità per crescere e imparare cose nuove.
Un Passo Alla Volta
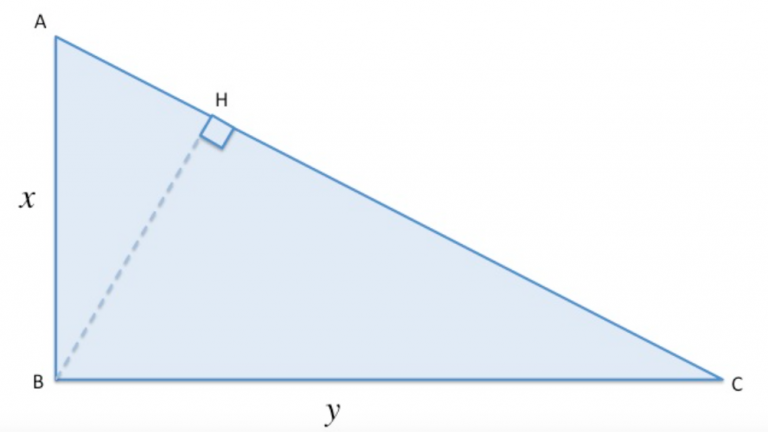
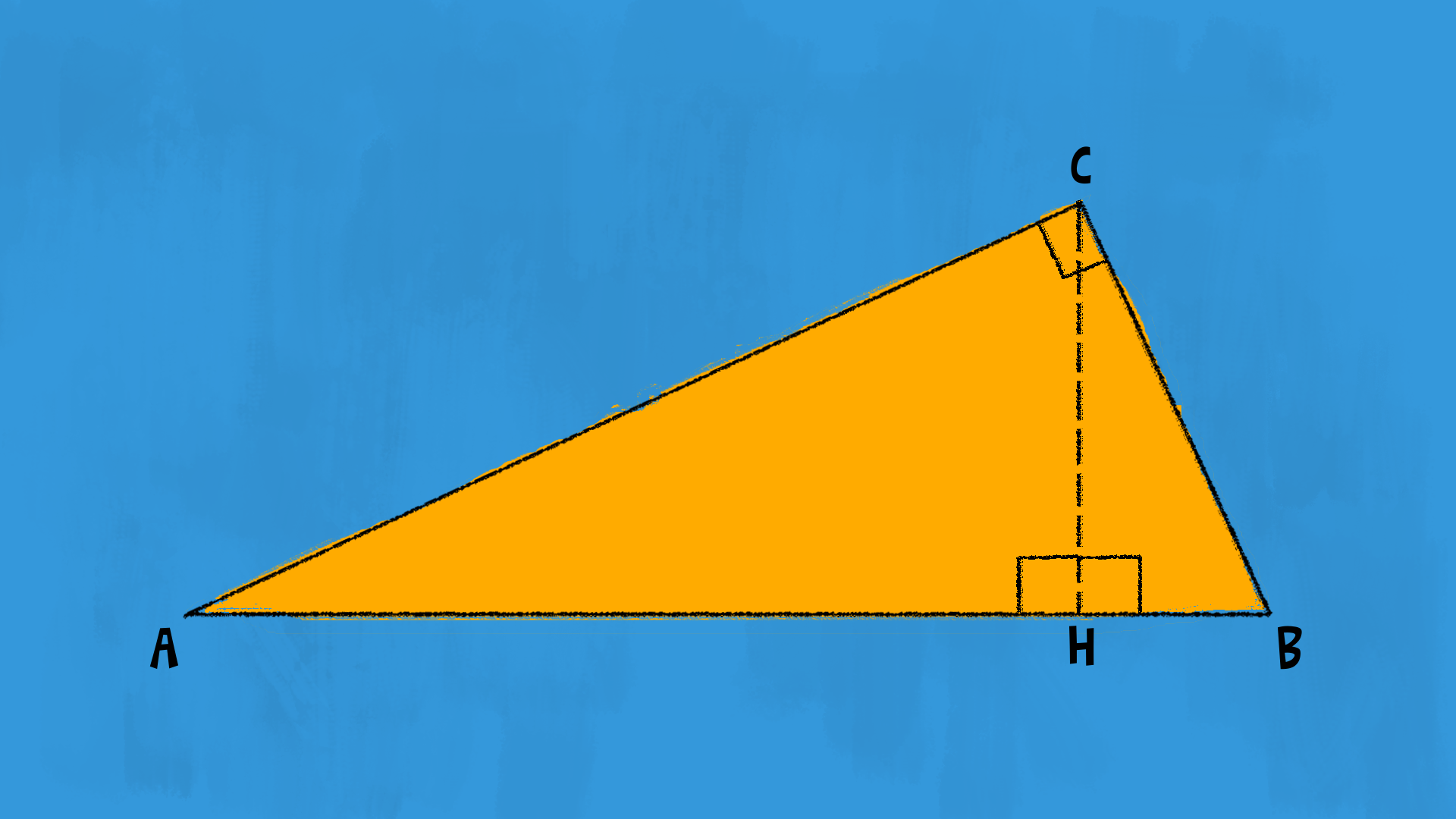
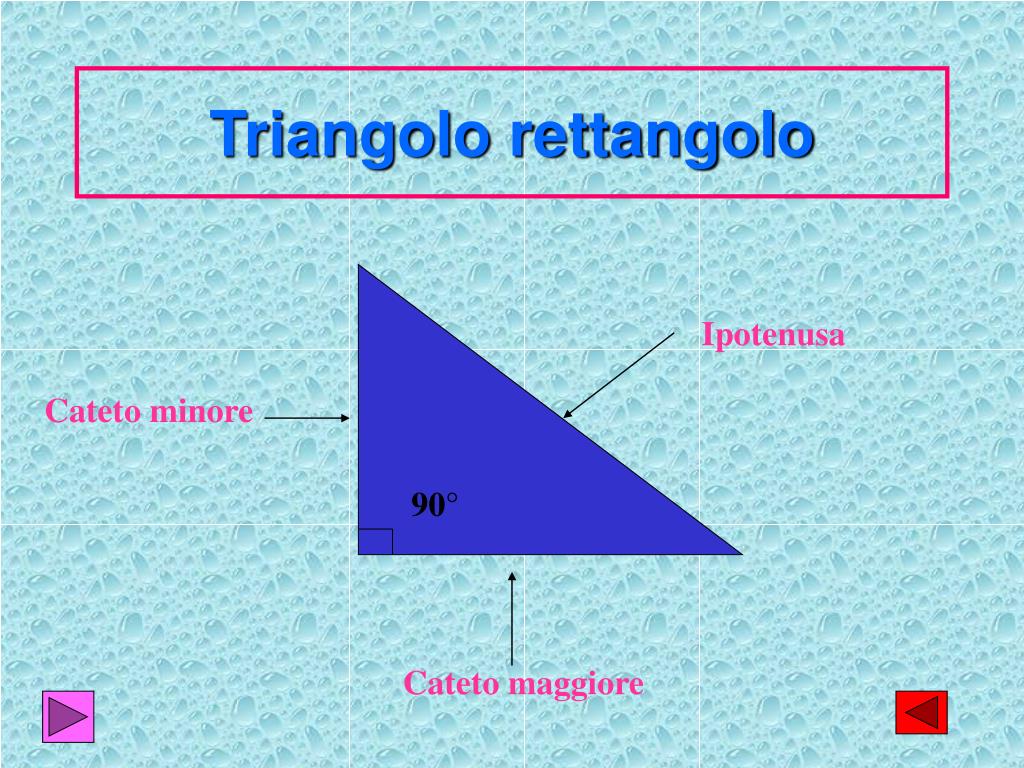
Immaginate un triangolo rettangolo, un po' come una fetta di pizza perfetta! L'ipotenusa è il lato più lungo, quello che si trova di fronte all'angolo retto. L'altezza relativa all'ipotenusa è la linea che parte dall'angolo retto e scende perpendicolarmente fino a toccare l'ipotenusa stessa. Il nostro obiettivo è scoprire quanto è lunga questa linea magica.
Ci sono diversi modi per farlo, come veri detective matematici! Uno dei metodi più comuni utilizza il teorema di Pitagora. Ricordate A al quadrato più B al quadrato uguale C al quadrato? Bene, possiamo usarlo anche qui! Dobbiamo solo essere un po' creativi e dividere il nostro triangolo rettangolo in due triangoli più piccoli, anch'essi rettangoli.
La Chiave è la Similitudine
Un'altra strategia brillante si basa sulla somiglianza dei triangoli. I triangoli che si formano quando tracciamo l'altezza relativa all'ipotenusa sono simili al triangolo originale. Questo significa che i loro angoli sono uguali e i loro lati sono proporzionali. Usando le proporzioni, possiamo calcolare l'altezza in modo rapido e preciso.
Non scoraggiatevi se all'inizio vi sembra difficile. La geometria, come la vita, richiede pratica e pazienza. Ricordate Einstein, che diceva: "Non ho particolari talenti. Sono solo appassionatamente curioso." La curiosità è la chiave per sbloccare ogni conoscenza!
"La matematica è la regina delle scienze e l'aritmetica è la regina della matematica." - Carl Friedrich Gauss
Lezioni per la Vita Scolastica
Ma cosa c'entra tutto questo con la vostra vita scolastica quotidiana? Molto più di quanto pensiate! Imparare a trovare l'altezza relativa all'ipotenusa vi insegna a scomporre problemi complessi in parti più piccole e gestibili. Vi insegna a usare gli strumenti a vostra disposizione (come il teorema di Pitagora) in modo creativo. Vi insegna a persistere, anche quando le cose si fanno difficili.
Ogni volta che vi trovate di fronte a un compito difficile, ricordatevi di questo triangolo. Scomponetelo, cercate le similitudini, usate gli strumenti che avete imparato. E soprattutto, non abbiate paura di chiedere aiuto! Nessuno si aspetta che siate perfetti, ma tutti si aspettano che proviate a fare del vostro meglio.
L'apprendimento è un viaggio, non una destinazione. Ogni piccolo passo avanti, ogni problema risolto, è una vittoria. E ogni volta che superate una sfida, diventate più forti e più capaci. Come diceva Nelson Mandela: "L'istruzione è l'arma più potente che puoi usare per cambiare il mondo."
Mantenere la Motivazione
Come rimanere motivati durante questo viaggio? Trovate la bellezza nella matematica! Cercate le connessioni tra la geometria e il mondo che vi circonda. Studiate con amici, condividete le vostre scoperte, aiutatevi a vicenda. E ricordatevi sempre perché state studiando: per realizzare i vostri sogni, per diventare persone migliori, per fare la differenza nel mondo.
Ogni esercizio risolto, ogni teorema compreso, è un mattone che costruisce il vostro futuro. Non sottovalutate il potere della disciplina e dell'impegno. Come diceva Vince Lombardi: "La pratica non rende perfetti. La pratica perfetta rende perfetti."
Quindi, la prossima volta che vedrete un triangolo rettangolo, ricordatevi di questa avventura. Ricordatevi che siete capaci di risolvere qualsiasi problema, che avete il potere di imparare e crescere, e che il futuro è nelle vostre mani. Forza e coraggio!