Come Si Trova L Altezza Di Un Rombo

Ciao! Capisco perfettamente come la geometria, e in particolare i rombi, possano sembrare un po' ostici a volte. Niente panico! Molti studenti si sentono così all'inizio. Ma ti assicuro, una volta compresi i concetti fondamentali, calcolare l'altezza di un rombo diventerà un gioco da ragazzi. Sono qui per guidarti passo dopo passo, con spiegazioni chiare e tanti esempi pratici.

Cos'è un Rombo e Perché l'Altezza è Importante?

Innanzitutto, rinfreschiamo la memoria su cosa sia un rombo. Un rombo è un quadrilatero, ovvero una figura geometrica con quattro lati, con queste caratteristiche principali:

• Tutti e quattro i lati sono congruenti, cioè hanno la stessa lunghezza.
• I lati opposti sono paralleli tra loro.
• Gli angoli opposti sono congruenti, mentre gli angoli adiacenti sono supplementari (la loro somma fa 180 gradi).
• Le diagonali si bisecano (si tagliano a metà) perpendicolarmente.

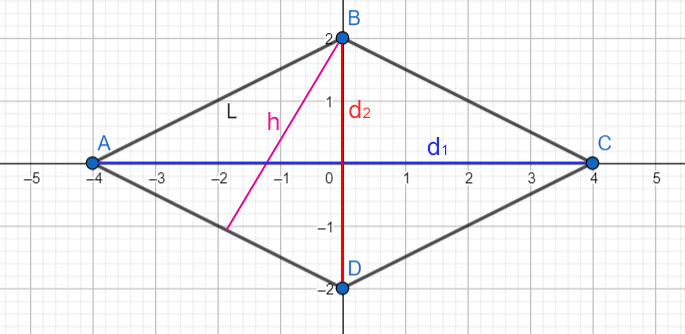
Ora, perché l'altezza è importante? Beh, l'altezza è la distanza perpendicolare tra due lati paralleli. Conoscere l'altezza è fondamentale per calcolare l'area del rombo, una misura importantissima in tantissime applicazioni pratiche, dall'architettura all'artigianato.

Metodi per Calcolare l'Altezza di un Rombo

Esistono diversi modi per trovare l'altezza di un rombo, a seconda delle informazioni che hai a disposizione. Esploriamoli uno per uno:

1. Conoscendo l'Area e la Lunghezza di un Lato

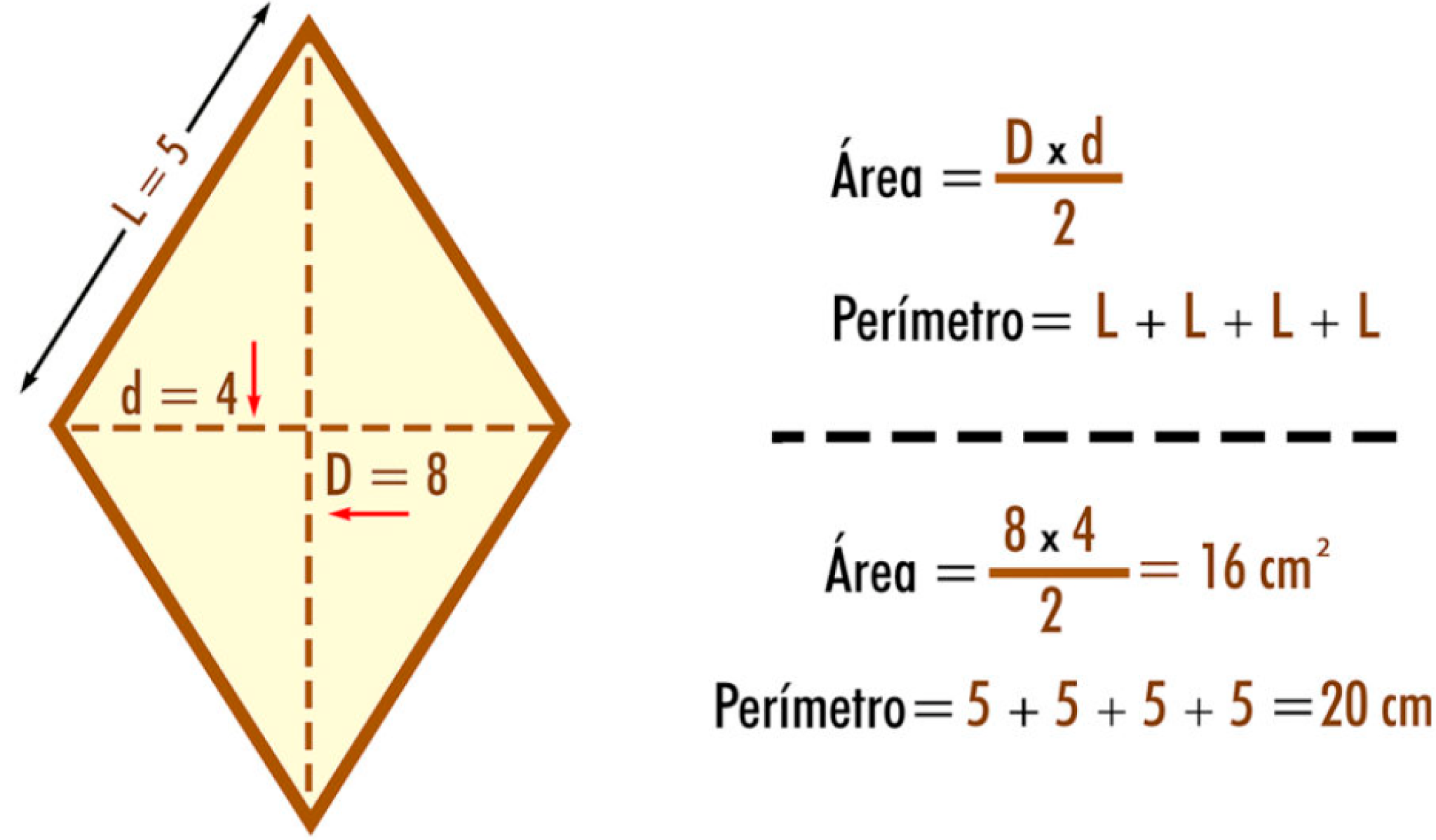
Questo è forse il metodo più diretto. Ricorda che l'area di un rombo si calcola come:

Area = base × altezza

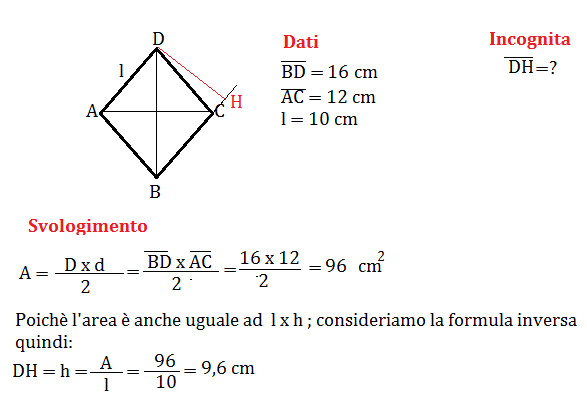
Dove la "base" è uno qualsiasi dei lati del rombo (dato che sono tutti uguali). Quindi, se conosci l'area (A) e la lunghezza del lato (l), puoi ricavare l'altezza (h) con questa formula:

h = A / l

Esempio pratico: Supponiamo di avere un rombo con un'area di 36 cm² e un lato lungo 6 cm. L'altezza sarà:

h = 36 cm² / 6 cm = 6 cm

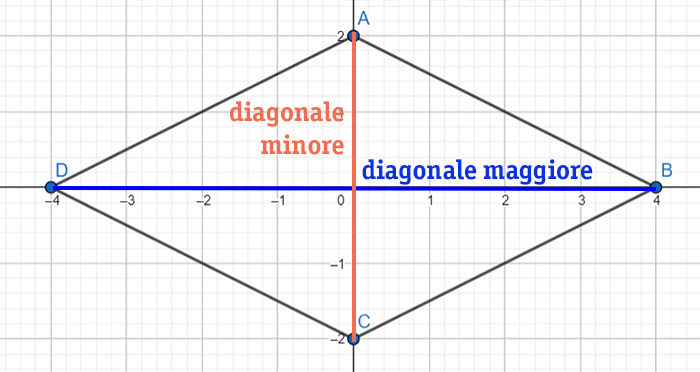
2. Conoscendo le Diagonali

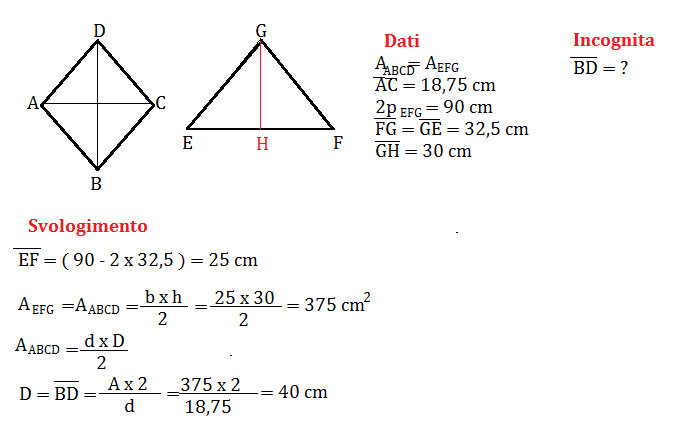
Se conosci la lunghezza delle due diagonali (d1 e d2), puoi calcolare l'area del rombo con la seguente formula:

Area = (d1 × d2) / 2

Una volta calcolata l'area, puoi utilizzare il metodo precedente (Area / lato) per trovare l'altezza, a patto di conoscere la lunghezza del lato! Se non conosci il lato, dovrai calcolarlo prima.

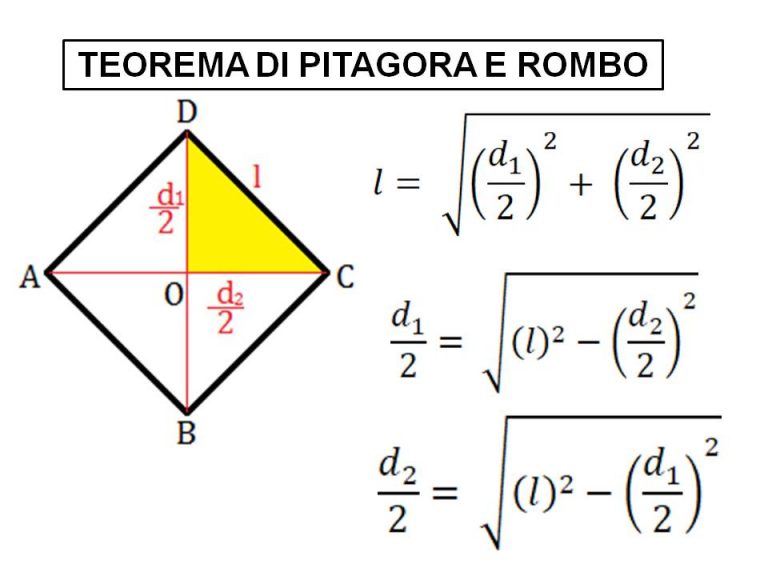
Come calcolare il lato se conosci le diagonali: Ricorda che le diagonali di un rombo si bisecano perpendicolarmente. Questo significa che dividono il rombo in quattro triangoli rettangoli congruenti. Puoi utilizzare il teorema di Pitagora per trovare la lunghezza del lato (che è l'ipotenusa di uno di questi triangoli):

lato = √( (d1/2)² + (d2/2)² )

Esempio pratico: Supponiamo che le diagonali misurino 8 cm e 6 cm rispettivamente. Calcoliamo il lato:

lato = √( (8/2)² + (6/2)² ) = √(4² + 3²) = √(16 + 9) = √25 = 5 cm

Ora calcoliamo l'area:

Area = (8 cm × 6 cm) / 2 = 24 cm²

Infine, l'altezza:

h = 24 cm² / 5 cm = 4.8 cm

3. Conoscendo un Angolo e un Lato

Se conosci la lunghezza di un lato (l) e uno degli angoli del rombo (ad esempio, θ), puoi utilizzare la trigonometria per trovare l'altezza. Ricorda che gli angoli opposti di un rombo sono uguali, e gli angoli adiacenti sono supplementari.

L'altezza può essere calcolata con la seguente formula:

h = l × sin(θ)

Dove sin(θ) è il seno dell'angolo θ. Assicurati che la tua calcolatrice sia impostata sulla modalità "gradi" (DEG) se l'angolo è espresso in gradi.

Esempio pratico: Supponiamo di avere un rombo con un lato di 7 cm e un angolo di 60 gradi.

h = 7 cm × sin(60°) ≈ 7 cm × 0.866 ≈ 6.06 cm

Esercizi Pratici per Allenarti

Ecco alcuni esercizi per mettere in pratica quello che hai imparato. Non aver paura di sbagliare! L'importante è provare.

1. Un rombo ha un'area di 48 cm² e un lato di 8 cm. Calcola l'altezza.
2. Le diagonali di un rombo misurano 10 cm e 12 cm. Calcola l'altezza.
3. Un rombo ha un lato di 5 cm e un angolo di 45 gradi. Calcola l'altezza.

Consiglio: Disegna sempre il rombo! Visualizzare il problema ti aiuterà a capire meglio quali informazioni hai a disposizione e quale metodo applicare.

Suggerimenti e Trucchi

• Controlla sempre le unità di misura: Assicurati che tutte le misure siano espresse nella stessa unità (ad esempio, cm, metri, etc.) prima di effettuare i calcoli.
• Sfrutta le proprietà del rombo: Ricorda che tutti i lati sono uguali e le diagonali si bisecano perpendicolarmente. Queste informazioni possono essere utili per risolvere problemi complessi.
• Utilizza una calcolatrice scientifica: Soprattutto quando devi calcolare il seno di un angolo.
• Chiedi aiuto se hai bisogno: Non esitare a chiedere al tuo insegnante, ai tuoi compagni o a me se hai difficoltà. Siamo qui per supportarti!

Perché è Importante Sapere Trovare l'Altezza di un Rombo?

Potresti chiederti: "Ma quando mi servirà mai sapere calcolare l'altezza di un rombo nella vita reale?". Beh, ecco alcuni esempi:

• Architettura: Gli architetti utilizzano le proprietà dei rombi per progettare strutture e pavimentazioni.
• Design: I designer utilizzano i rombi per creare motivi e decorazioni.
• Artigianato: Gli artigiani utilizzano i rombi per realizzare gioielli, tessuti e altri oggetti.
• Matematica: La comprensione dei rombi è fondamentale per sviluppare una solida base in geometria, che è essenziale per studi più avanzati in matematica, fisica e ingegneria.

Come dice la Prof.ssa Rossi, insegnante di matematica da oltre 20 anni: "Comprendere le figure geometriche come il rombo non è solo questione di formule, ma di sviluppare un pensiero logico e spaziale che sarà utile in molteplici aspetti della vita."

Un Ultimo Incoraggiamento

La geometria può sembrare complicata all'inizio, ma con la pratica e la perseveranza, diventerà sempre più facile. Non arrenderti mai! Ogni volta che risolvi un problema, stai allenando il tuo cervello e sviluppando le tue capacità di problem-solving. Credi in te stesso e nelle tue capacità!

Spero che questa guida ti sia stata utile. Se hai domande o vuoi approfondire ulteriormente l'argomento, non esitare a scrivermi! Sono qui per aiutarti a raggiungere il successo.

In bocca al lupo per i tuoi studi!