Come Si Trova L Altezza Di Un Prisma

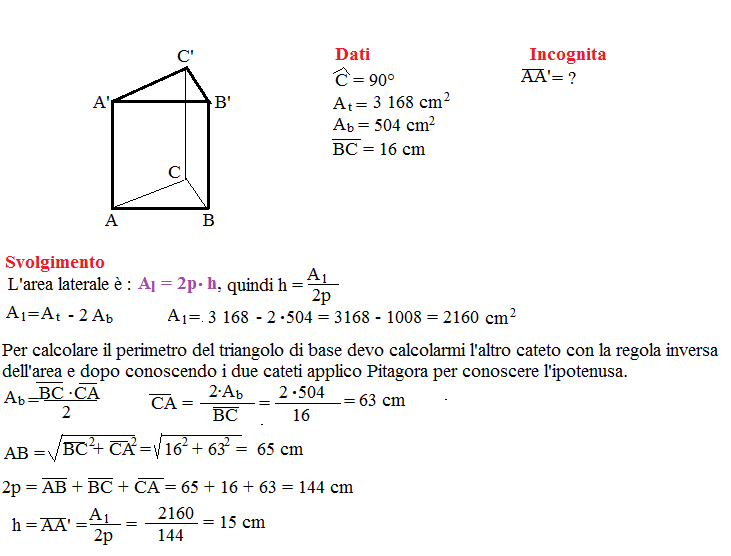
Capita a tutti di sentirsi un po' persi di fronte alla geometria, specialmente quando si tratta di figure tridimensionali come i prismi. Non preoccuparti, trovare l'altezza di un prisma può sembrare complicato all'inizio, ma con la giusta guida e un po' di pratica, diventerà un gioco da ragazzi! Questo articolo è qui per aiutarti a superare qualsiasi difficoltà e a comprendere appieno questo concetto.

Cos'è un Prisma e Perché è Importante Conoscere la Sua Altezza?

Prima di addentrarci nei metodi per calcolare l'altezza, cerchiamo di capire cos'è un prisma. Un prisma è un solido geometrico con due facce parallele e congruenti, chiamate basi, collegate da facce laterali che sono parallelogrammi. Pensa a una scatola di scarpe: quella è un esempio di prisma (in particolare, un prisma rettangolare).

L'altezza del prisma è la distanza perpendicolare tra le sue due basi. Conoscere l'altezza è fondamentale per calcolare il volume (lo spazio occupato dal prisma) e l'area della superficie totale. Queste grandezze sono cruciali in molti campi, dall'architettura all'ingegneria, dalla fisica alla chimica. Immagina di dover calcolare la quantità di materiale necessaria per costruire un edificio a forma di prisma: conoscere l'altezza è essenziale!

Le Basi Contano: Riconoscere il Tipo di Prisma

I prismi si classificano in base alla forma delle loro basi: prisma triangolare (base a forma di triangolo), prisma quadrato (base a forma di quadrato), prisma pentagonale (base a forma di pentagono) e così via. Questa classificazione è importante perché influisce sul modo in cui calcoliamo l'area della base, un valore necessario per determinare l'altezza in alcuni casi.

Come Trovare l'Altezza di un Prisma: Diversi Approcci

Esistono diversi modi per trovare l'altezza di un prisma, a seconda delle informazioni che abbiamo a disposizione. Vediamo i metodi più comuni:

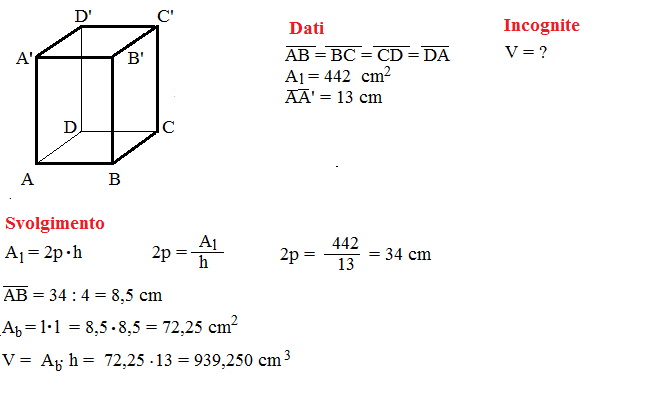
Metodo 1: Conoscendo il Volume e l'Area della Base

Questo è il metodo più diretto. Se conosciamo il volume (V) del prisma e l'area della base (Ab), possiamo utilizzare la seguente formula:

Altezza (h) = Volume (V) / Area della base (Ab)

Esempio: Supponiamo di avere un prisma con un volume di 120 cm³ e un'area della base di 24 cm². L'altezza sarà: h = 120 cm³ / 24 cm² = 5 cm.

Consiglio pratico: Assicurati che le unità di misura del volume e dell'area della base siano coerenti (es. cm³ e cm², m³ e m²). In caso contrario, dovrai prima convertirle.

Metodo 2: Utilizzando il Teorema di Pitagora (per Prismi Rettangolari Speciali)

Questo metodo si applica in situazioni specifiche, ovvero quando conosciamo la lunghezza di un lato della base, la diagonale della base e un'altra dimensione del prisma, formando un triangolo rettangolo. In questi casi, possiamo utilizzare il Teorema di Pitagora (a² + b² = c²) per trovare l'altezza. Questo richiede un'attenta osservazione della geometria del problema.

Esempio: Immagina un prisma rettangolare dove la diagonale della base è di 13 cm, un lato della base è di 5 cm, e devi trovare l'altezza. Prima calcoli l'altro lato della base usando il teorema di Pitagora: b² = 13² - 5² = 144, quindi b = 12 cm. A questo punto, se ti viene fornita una diagonale che coinvolge anche l'altezza, puoi applicare nuovamente il teorema di Pitagora per trovarla.

Ricorda: Il Teorema di Pitagora si applica solo ai triangoli rettangoli. Assicurati che la figura geometrica formata dalle dimensioni che conosci sia effettivamente un triangolo rettangolo.

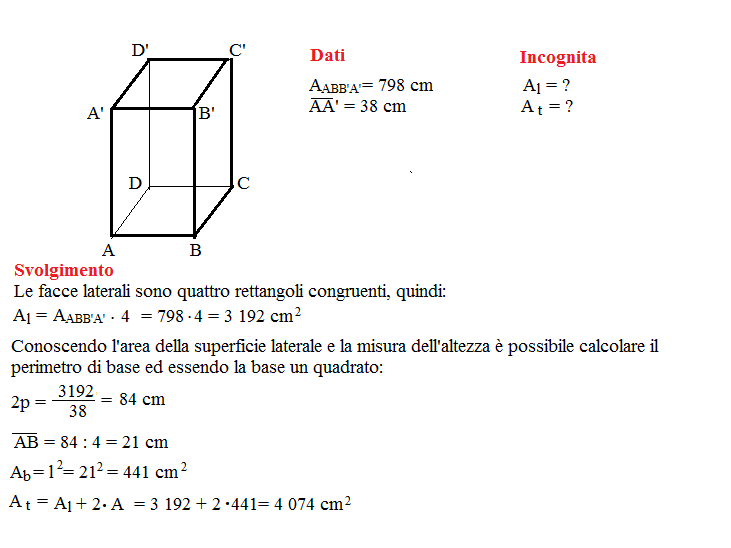
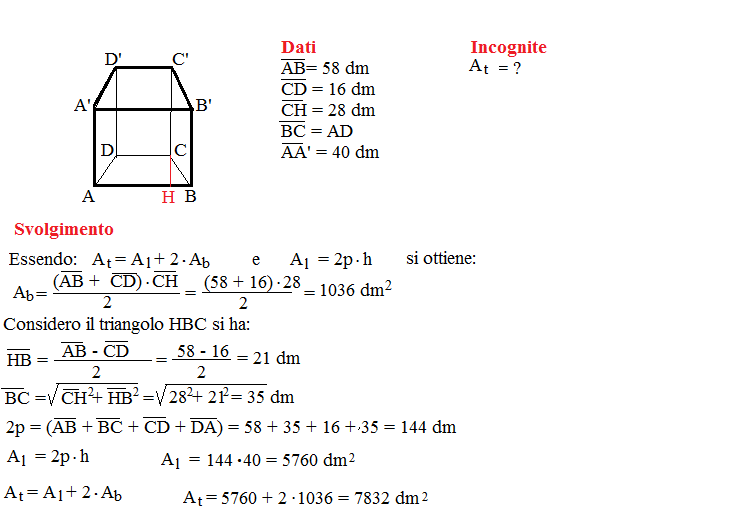
Metodo 3: Conoscendo l'Area della Superficie Laterale e il Perimetro della Base

Se conosciamo l'area della superficie laterale (Al) e il perimetro della base (Pb), possiamo utilizzare la seguente formula:

Altezza (h) = Area della superficie laterale (Al) / Perimetro della base (Pb)

Esempio: Supponiamo di avere un prisma con un'area della superficie laterale di 80 cm² e un perimetro della base di 20 cm. L'altezza sarà: h = 80 cm² / 20 cm = 4 cm.

Importante: L'area della superficie laterale si riferisce solo all'area delle facce laterali, escluse le basi.

Metodo 4: Utilizzo di Angoli e Trigonometria

In alcuni problemi, potresti avere a disposizione degli angoli e la lunghezza di uno spigolo del prisma. In questi casi, la trigonometria (seno, coseno, tangente) può essere utile per determinare l'altezza. Questo metodo è più avanzato e richiede una buona conoscenza delle funzioni trigonometriche.

Esempio: Se conosci l'angolo tra una faccia laterale e la base, e la lunghezza di uno spigolo laterale, puoi utilizzare la funzione seno per calcolare l'altezza: h = lunghezza dello spigolo * sin(angolo).

Attenzione: Assicurati che la calcolatrice sia impostata sulla modalità corretta (gradi o radianti) a seconda dell'unità di misura dell'angolo.

Consigli Pratici per Studenti e Insegnanti

Per gli Studenti:

Per gli Insegnanti:

Studi dimostrano che l'apprendimento pratico e l'utilizzo di supporti visivi migliorano significativamente la comprensione dei concetti geometrici. (Fonte: National Council of Teachers of Mathematics - NCTM)

Superare le Difficoltà Comuni

Alcune difficoltà comuni che gli studenti incontrano quando calcolano l'altezza di un prisma includono:

Per superare queste difficoltà, è importante prestare attenzione ai dettagli, controllare le unità di misura, rivedere le formule e fare molta pratica.

Conclusione: La Geometria è Accessibile a Tutti!

Trovare l'altezza di un prisma può sembrare una sfida all'inizio, ma con gli strumenti giusti, la pratica e un po' di determinazione, è un obiettivo raggiungibile. Ricorda, la geometria non è solo un insieme di formule, ma un modo per comprendere e interpretare il mondo che ci circonda. Non arrenderti di fronte alle difficoltà, chiedi aiuto quando ne hai bisogno e continua a esplorare le meraviglie della matematica!

Con impegno e dedizione, puoi padroneggiare l'arte di calcolare l'altezza di un prisma e aprire le porte a un mondo di scoperte geometriche! In bocca al lupo!