Come Si Trova Il Codominio Di Una Funzione

Ti sei mai trovato di fronte a una funzione matematica, sentendoti un po' spaesato, soprattutto quando si trattava di capire cos'è esattamente il codominio? Non sei solo! Molti studenti, genitori che cercano di aiutare i propri figli con i compiti, e persino alcuni insegnanti a volte trovano questo concetto un po' ostico. La matematica, si sa, può sembrare una lingua straniera, ma con la giusta guida e un approccio chiaro, anche le sfide più grandi diventano superabili. Cerchiamo di rendere questo viaggio nel mondo delle funzioni e del loro codominio un'esperienza meno intimidatoria e più illuminante.

Cos'è il Codominio? Una Definizione Chiaro e Semplice

Partiamo dalle basi. Immagina una funzione come una macchina: tu ci metti qualcosa dentro (l'input, o valore del dominio) e la macchina produce qualcos'altro (l'output, o valore dell'immagine). Il codominio, invece, è l'insieme di tutti i possibili output che la macchina *potrebbe* produrre. Attenzione, non è detto che la macchina produca *ogni* valore nel codominio, ma è l'insieme di tutte le possibili "destinazioni".

Per capirlo meglio, facciamo un esempio concreto:

Considera la funzione f(x) = x². Il dominio potrebbe essere l'insieme dei numeri reali (ℝ), cioè tutti i numeri che possiamo immaginare. Ora, il codominio *potrebbe* essere l'insieme dei numeri reali (ℝ) anch'esso. Tuttavia, l'immagine (l'insieme dei valori che la funzione *effettivamente* produce) è l'insieme dei numeri reali non negativi (ℝ⁺ ∪ {0}), perché un quadrato non può mai essere negativo. Quindi, in questo caso, l'immagine è un sottoinsieme del codominio.

In sintesi:

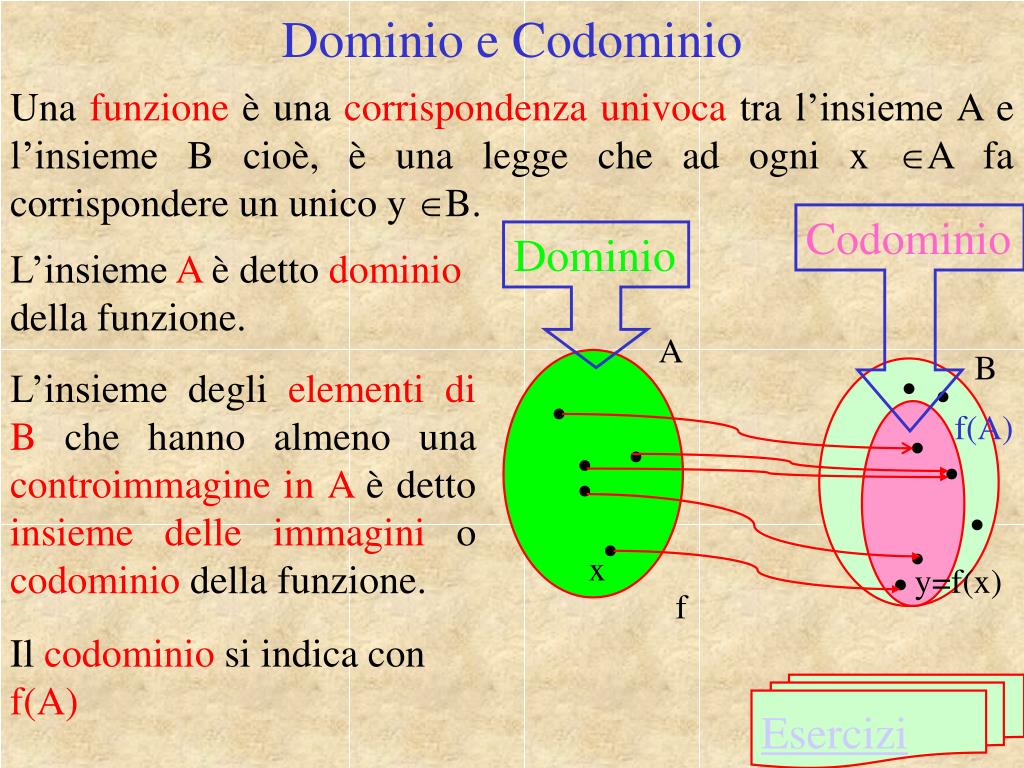
• Dominio: L'insieme di tutti i possibili input di una funzione.
• Codominio: L'insieme di tutti i possibili output di una funzione.
• Immagine (o Range): L'insieme di tutti gli output *effettivi* prodotti dalla funzione quando si applica a tutti i valori del dominio. L'immagine è sempre un sottoinsieme del codominio.

Come Trovare il Codominio: Passo Dopo Passo

A differenza del dominio, che spesso richiede un'analisi approfondita per escludere valori problematici (come divisioni per zero o radici di numeri negativi), il codominio è spesso *definito* dalla funzione stessa o dal contesto del problema. Questo significa che, in molti casi, il codominio ti viene dato!

1. Leggi Attentamente il Problema

Il primo passo è sempre leggere attentamente il problema o la definizione della funzione. Spesso, il codominio è esplicitamente indicato. Ad esempio, potresti trovare frasi come: "Sia f: ℝ → ℝ una funzione...", che indica chiaramente che sia il dominio che il codominio sono l'insieme dei numeri reali.

2. Se il Codominio Non è Esplicito, Cerca Indizi nel Contesto

Se il problema non specifica esplicitamente il codominio, cerca indizi nel contesto. Ad esempio, se la funzione rappresenta l'altezza di una pianta nel tempo, il codominio potrebbe essere l'insieme dei numeri reali non negativi (ℝ⁺ ∪ {0}), poiché l'altezza non può essere negativa.

3. Considera il Tipo di Funzione

Il tipo di funzione può fornire utili informazioni sul codominio. Ecco alcuni esempi:

• Funzioni polinomiali: Se non specificato diversamente, il codominio è spesso l'insieme dei numeri reali (ℝ).
• Funzioni esponenziali: Se la base è positiva, il codominio è l'insieme dei numeri reali positivi (ℝ⁺).
• Funzioni trigonometriche (seno e coseno): Il codominio è l'intervallo [-1, 1].
• Funzioni logaritmiche: Se non specificato diversamente, il codominio è l'insieme dei numeri reali (ℝ).
• Funzioni con radici quadrate: Se non specificato diversamente, il codominio è l'insieme dei numeri reali non negativi (ℝ⁺ ∪ {0}).

4. Distingui tra Codominio e Immagine

È fondamentale distinguere tra codominio e immagine. Come abbiamo detto, il codominio è l'insieme di tutti i *possibili* output, mentre l'immagine è l'insieme degli output *effettivi*. Determinare l'immagine può essere più complesso e spesso richiede l'analisi del comportamento della funzione.

Esempio:

Sia f(x) = sin(x), con dominio ℝ e codominio ℝ. L'immagine è l'intervallo [-1, 1]. Il codominio è ℝ, ma la funzione non assume tutti i valori reali; si limita a oscillare tra -1 e 1.

Esempi Pratici: Dal Quaderno alla Vita Reale

Vediamo alcuni esempi pratici per consolidare la comprensione:

Esempio 1:

Un'azienda produce magliette. La funzione f(x) rappresenta il costo totale di produzione di x magliette. Il dominio è l'insieme dei numeri interi non negativi (ℕ ∪ {0}) (non puoi produrre un numero negativo di magliette). Il codominio potrebbe essere l'insieme dei numeri reali non negativi (ℝ⁺ ∪ {0}), dato che il costo non può essere negativo. L'immagine dipenderà dalla funzione specifica del costo, ma sarà sempre un sottoinsieme del codominio.

Esempio 2:

Un termometro misura la temperatura in gradi Celsius. La funzione f(t) rappresenta la temperatura al tempo t. Il dominio potrebbe essere un intervallo di tempo specifico, ad esempio [0, 24] ore. Il codominio potrebbe essere un intervallo di temperature ragionevoli per l'ambiente in cui si trova il termometro, ad esempio [-20, 40] gradi Celsius. L'immagine dipenderà dalle effettive temperature registrate durante quel periodo di tempo.

Esempio 3 (Esempio classroom):

Un insegnante vuole creare una funzione che assegni un voto (da 1 a 10) a ogni studente in base al numero di esercizi corretti fatti. Chiamiamo la funzione g(n), dove n è il numero di esercizi corretti fatti. In questo caso:

• Il dominio è l'insieme di tutti gli studenti.
• Il codominio è l'insieme di tutti i voti possibili: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
• L'immagine è l'insieme di tutti i voti effettivamente assegnati agli studenti.

L'immagine potrebbe essere {5, 6, 7, 8, 9}, in questo caso nessuno ha preso 1,2,3,4 o 10. Questo dimostra che l'immagine è un sottoinsieme del codominio.

Errori Comuni da Evitare

Ecco alcuni errori comuni che gli studenti commettono quando si tratta di codominio:

• Confondere codominio e immagine: Ricorda, il codominio è l'insieme di *tutti i possibili* output, mentre l'immagine è l'insieme degli output *effettivi*.
• Ignorare il contesto del problema: Il contesto può fornire indizi importanti sul codominio.
• Non leggere attentamente la definizione della funzione: Il codominio potrebbe essere esplicitamente indicato nella definizione.

Consigli Aggiuntivi per Insegnanti e Genitori

Per gli insegnanti:

• Utilizza esempi concreti e rilevanti per gli studenti.
• Enfatizza la differenza tra codominio e immagine.
• Chiarisci che il codominio è spesso definito dalla funzione o dal problema.
• Incoraggia gli studenti a porre domande e a discutere i concetti.

Per i genitori:

• Aiuta tuo figlio a leggere attentamente il problema e a identificare le informazioni chiave.
• Spiega la differenza tra codominio e immagine in termini semplici.
• Utilizza esempi della vita reale per illustrare il concetto.
• Sii paziente e incoraggiante!

Conclusione

Comprendere il codominio di una funzione è un passo fondamentale per padroneggiare il concetto di funzione stesso. Sebbene possa sembrare un po' astratto all'inizio, con la giusta guida, la pratica e un po' di pazienza, diventerà un concetto chiaro e intuitivo. Ricorda, la matematica è un linguaggio che richiede tempo e dedizione per essere appreso. Non aver paura di fare domande, di esplorare e di sperimentare. E soprattutto, non dimenticare che l'apprendimento è un viaggio, non una destinazione!