Come Si Studia Il Segno Di Una Funzione
Ciao! Se sei qui, probabilmente stai lottando con lo studio del segno di una funzione. Non preoccuparti, è un argomento che all'inizio può sembrare ostico, ma con la giusta guida e un po' di pratica, diventerà molto più chiaro. Molti studenti si sentono frustrati quando vedono espressioni matematiche complesse e non sanno da dove cominciare. L'obiettivo di questo articolo è di offrirti un approccio strutturato e comprensibile per superare queste difficoltà.
Capita a tutti di sentirsi persi di fronte a un problema di matematica. Ricorda, la chiave è scomporre il problema in passaggi più piccoli e gestibili. Iniziamo!
Perché Studiare il Segno di una Funzione è Importante?
Forse ti stai chiedendo: "Ma a cosa serve davvero studiare il segno di una funzione?". La risposta è che ha applicazioni pratiche in molti campi. Immagina di essere un ingegnere che progetta un ponte. Conoscere il segno di una funzione che descrive la forza su una parte del ponte è cruciale per assicurarsi che la struttura sia stabile e sicura. Oppure, pensa a un economista che analizza l'andamento di un'azienda: il segno di una funzione può indicare periodi di profitto (segno positivo) o perdita (segno negativo).
Ecco alcuni esempi concreti:
- Ingegneria: Calcolo delle tensioni e delle deformazioni strutturali.
- Economia: Analisi dei profitti e delle perdite di un'azienda.
- Fisica: Studio del moto di un oggetto, determinando quando la velocità è positiva (si muove in avanti) o negativa (si muove all'indietro).
- Statistica: Interpretazione dei risultati di un modello statistico, identificando le relazioni positive o negative tra le variabili.
Quindi, non si tratta solo di un esercizio accademico, ma di uno strumento potente per risolvere problemi reali.
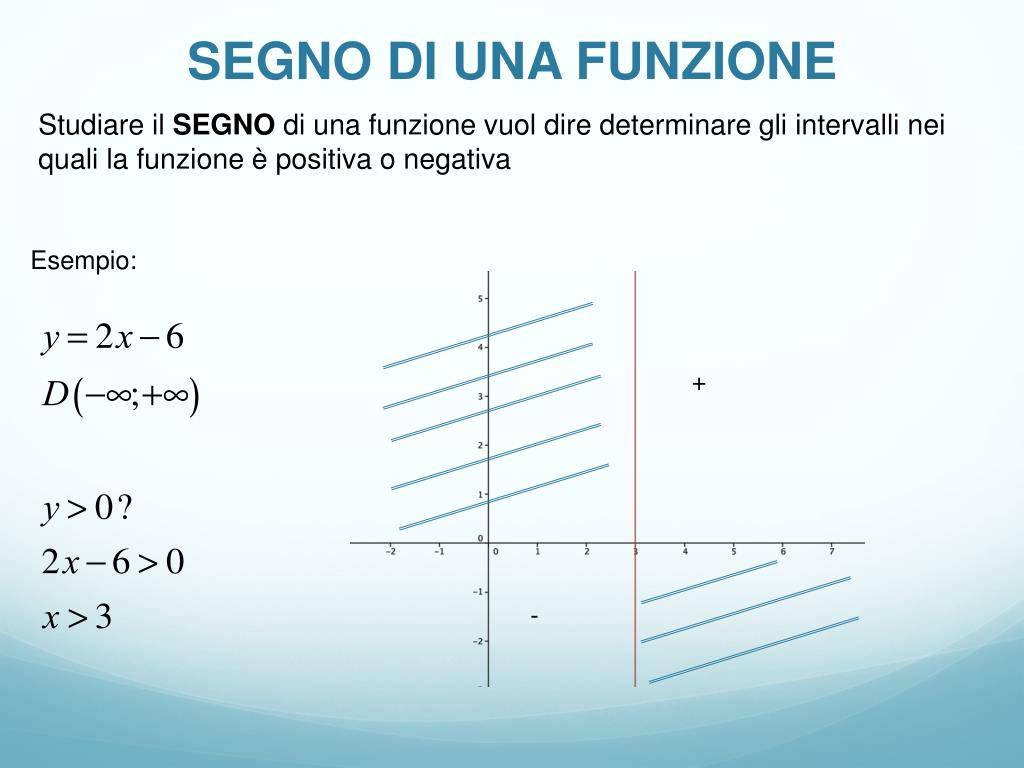
Cosa Significa Studiare il Segno di una Funzione?
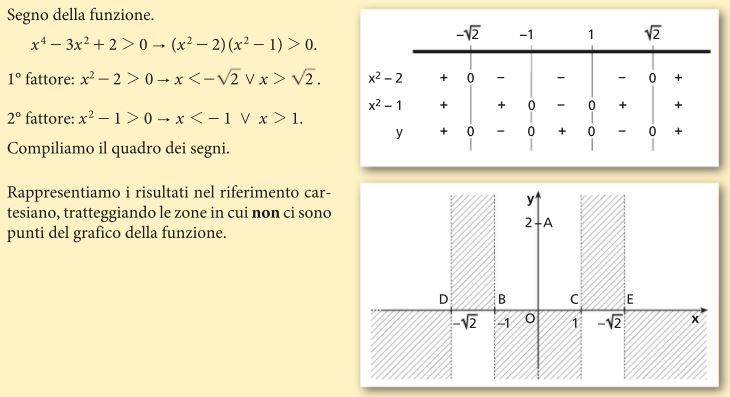
Studiare il segno di una funzione f(x) significa determinare per quali valori di x la funzione è positiva (f(x) > 0), negativa (f(x) < 0) o nulla (f(x) = 0). In altre parole, vogliamo capire dove il grafico della funzione si trova sopra l'asse delle x, sotto l'asse delle x o interseca l'asse delle x.
Possiamo rappresentare graficamente queste informazioni sulla retta reale. Ad esempio, se f(x) > 0 per x compreso tra 2 e 5, indicheremo questo intervallo con un segno "+". Se f(x) < 0 per x minore di 2 o maggiore di 5, indicheremo questi intervalli con un segno "-". I punti in cui f(x) = 0 (in questo caso x = 2 e x = 5) sono i punti di intersezione con l'asse x, anche detti zeri della funzione.
Come Si Fa: Passo Dopo Passo
Ecco una guida passo dopo passo per studiare il segno di una funzione:
1. Trovare gli Zeri della Funzione
Il primo passo è trovare i valori di x per cui f(x) = 0. Questi sono i punti in cui la funzione cambia segno. Risolvere l'equazione f(x) = 0 può richiedere diverse tecniche a seconda della complessità della funzione. Ad esempio, per un polinomio di secondo grado, puoi usare la formula quadratica. Per funzioni più complesse, potresti aver bisogno di metodi numerici o di factoring.
Esempio: Consideriamo la funzione f(x) = x² - 4. Per trovare gli zeri, dobbiamo risolvere x² - 4 = 0. Questo ci dà x = ±2. Quindi, gli zeri della funzione sono x = -2 e x = 2.
2. Determinare il Segno in Ogni Intervallo
Una volta trovati gli zeri, dividiamo la retta reale in intervalli utilizzando questi zeri come punti di divisione. Per la funzione dell'esempio precedente, abbiamo tre intervalli: (-∞, -2), (-2, 2) e (2, +∞). Ora, dobbiamo determinare il segno di f(x) in ciascuno di questi intervalli.
Per fare ciò, scegliamo un punto di prova all'interno di ogni intervallo e calcoliamo il valore di f(x) in quel punto. Il segno del risultato ci dirà il segno della funzione in tutto l'intervallo.
Esempio (continuazione):
- Intervallo (-∞, -2): Scegliamo x = -3. f(-3) = (-3)² - 4 = 9 - 4 = 5 > 0. Quindi, f(x) > 0 in questo intervallo.
- Intervallo (-2, 2): Scegliamo x = 0. f(0) = (0)² - 4 = -4 < 0. Quindi, f(x) < 0 in questo intervallo.
- Intervallo (2, +∞): Scegliamo x = 3. f(3) = (3)² - 4 = 9 - 4 = 5 > 0. Quindi, f(x) > 0 in questo intervallo.
3. Creare una Tabella dei Segni
Per organizzare le informazioni, è utile creare una tabella dei segni. Questa tabella mostra gli intervalli, i punti di prova, il segno di f(x) in ogni intervallo e gli zeri della funzione.
Esempio (continuazione):
| Intervallo | Punto di Prova | f(x) | Segno di f(x) |
|---|---|---|---|
| (-∞, -2) | x = -3 | 5 | + |
| (-2, 2) | x = 0 | -4 | - |
| (2, +∞) | x = 3 | 5 | + |
| Zeri | x = -2, x = 2 | 0 | 0 |
4. Interpretare i Risultati
Una volta completata la tabella dei segni, possiamo interpretare i risultati. Sappiamo che f(x) è positiva per x < -2 e x > 2, negativa per -2 < x < 2, e nulla per x = -2 e x = 2. Possiamo utilizzare queste informazioni per disegnare un grafico approssimativo della funzione.
Affrontare le Funzioni Più Complesse
Quando ci troviamo di fronte a funzioni più complesse, come quelle razionali (quozienti di polinomi) o quelle che coinvolgono radici quadrate, dobbiamo prestare attenzione a due cose:
- Denominatori: Dobbiamo assicurarci che il denominatore non sia mai uguale a zero, poiché la funzione non è definita in quei punti. Questi punti sono chiamati punti di discontinuità.
- Radici Quadrate: L'argomento di una radice quadrata deve essere sempre maggiore o uguale a zero, altrimenti la funzione non è definita nei numeri reali.
Per le funzioni razionali, seguiamo gli stessi passaggi di prima, ma includiamo anche i punti di discontinuità nella nostra tabella dei segni. Per le funzioni con radici quadrate, determiniamo prima il dominio della funzione (l'insieme dei valori di x per cui la funzione è definita) e poi procediamo come al solito.
Errori Comuni e Come Evitarli
Ecco alcuni errori comuni che gli studenti commettono quando studiano il segno di una funzione e come evitarli:
- Dimenticare di trovare gli zeri: È fondamentale trovare tutti gli zeri della funzione, altrimenti non divideremo correttamente la retta reale in intervalli.
- Sbagliare i calcoli: Un piccolo errore di calcolo può portare a un risultato completamente sbagliato. Ricontrolla sempre i tuoi calcoli!
- Non considerare i punti di discontinuità: Per le funzioni razionali, è cruciale identificare i punti di discontinuità e includerli nella tabella dei segni.
- Scegliere punti di prova sbagliati: Assicurati che il punto di prova che scegli sia effettivamente all'interno dell'intervallo che stai considerando.
- Confondere il segno della funzione con il segno di x: Stiamo studiando il segno di f(x), non il segno di x.
Un Contro-Argomento: L'Uso della Derivata Prima
Alcuni potrebbero sostenere che per studiare il segno di una funzione sia necessario calcolare la derivata prima per determinare gli intervalli di crescita e decrescita, e quindi dedurre il segno. Sebbene la derivata prima fornisca informazioni preziose sull'andamento della funzione, non è strettamente necessaria per determinare il segno. Il metodo descritto in questo articolo è più diretto e può essere applicato anche a funzioni per le quali non è facile calcolare la derivata o per le quali la derivata non esiste in tutti i punti.
Conclusione
Studiare il segno di una funzione può sembrare complicato all'inizio, ma con la giusta guida e un po' di pratica, puoi padroneggiare questa abilità. Ricorda di seguire i passaggi descritti in questo articolo, di prestare attenzione ai dettagli e di ricontrollare sempre i tuoi calcoli. Non aver paura di chiedere aiuto se hai bisogno di chiarimenti. La matematica è come un puzzle: ogni pezzo è importante per completare il quadro.
Ora che hai letto questa guida, ti senti più sicuro nell'affrontare lo studio del segno di una funzione? Qual è il prossimo problema che proverai a risolvere?