Come Si Fanno Le Radici Quadrate

Ciao! Se sei qui, probabilmente ti stai chiedendo: "Come si fanno le radici quadrate?". Non preoccuparti, è una domanda che in tanti si pongono! Magari ti ricordi le formule a memoria, ma capire il concetto dietro le radici quadrate è molto più importante. Molti studenti e genitori si sentono frustrati di fronte a questo argomento, ma ti assicuro che con un po' di pazienza e la giusta guida, diventerà tutto molto più chiaro.

L'obiettivo di questo articolo è proprio quello di demistificare le radici quadrate. Le affronteremo passo dopo passo, con esempi pratici e un linguaggio semplice, in modo che tu possa capire, applicare e persino divertirti con questo aspetto della matematica. Ricorda, la matematica è come un linguaggio: più la pratichi, più diventa fluente!

Cos'è una Radice Quadrata?

Immagina di avere un quadrato. La sua area è, diciamo, 9 centimetri quadrati. La radice quadrata di 9 è la lunghezza del lato di quel quadrato. Quindi, qual è il numero che, moltiplicato per se stesso, dà 9? La risposta è 3, perché 3 x 3 = 9. Perciò, la radice quadrata di 9 è 3.

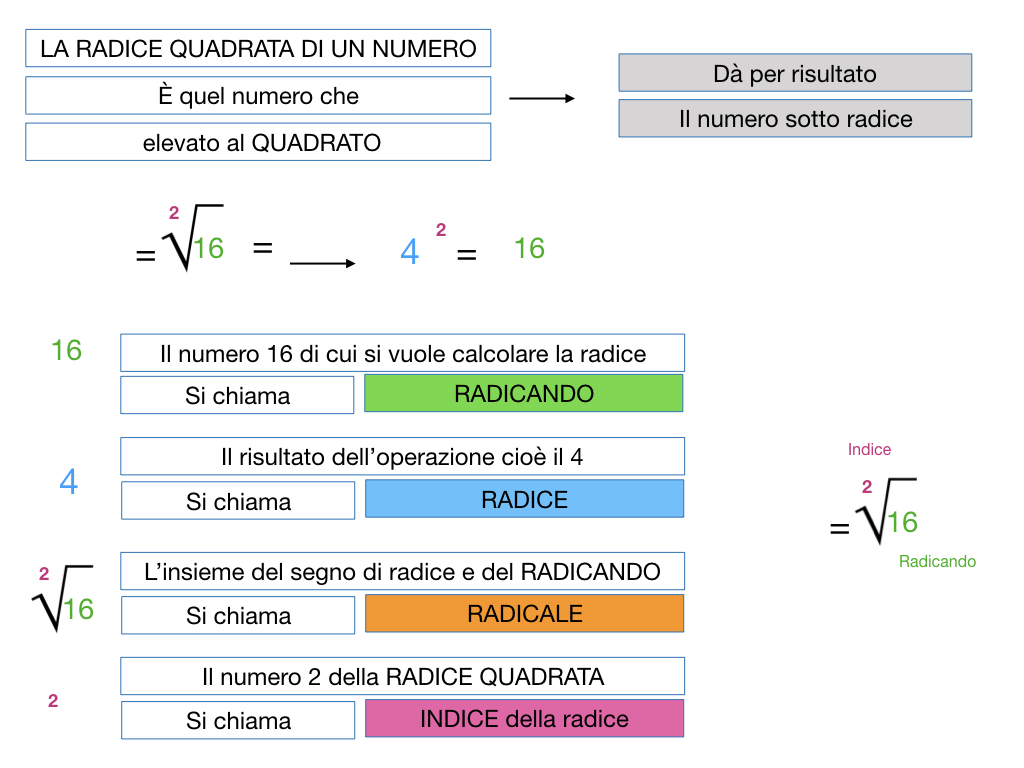
In termini matematici, la radice quadrata di un numero "a" è quel numero "b" che, elevato al quadrato (b x b), dà "a". Si scrive così: √a = b dove "√" è il simbolo della radice quadrata.

Esempio: √25 = 5 perché 5 x 5 = 25

"Molti studenti trovano difficile capire il concetto di radice quadrata perché spesso si concentrano solo sulla memorizzazione delle regole," afferma la professoressa Maria Rossi, insegnante di matematica da oltre 15 anni. "È fondamentale visualizzare cosa rappresenta la radice quadrata, ad esempio attraverso l'immagine del quadrato, per rendere il concetto più concreto."

Come Calcolare le Radici Quadrate: Metodi Semplici

Esistono diversi metodi per calcolare le radici quadrate. Partiamo dai più semplici e poi vediamo come affrontare numeri più grandi.

1. Radici Quadrate Perfette:

Le radici quadrate perfette sono quelle di numeri che sono il risultato di un numero intero moltiplicato per se stesso. Ad esempio, 4, 9, 16, 25, 36, 49, 64, 81, 100 sono tutti quadrati perfetti.

Esempio: √49 = 7 perché 7 x 7 = 49

Esercizio: Prova a trovare la radice quadrata di questi numeri: √16, √64, √81, √100.

2. Scomposizione in Fattori Primi (per numeri più grandi):

Questo metodo è utile per calcolare la radice quadrata di numeri che non sono immediatamente riconoscibili come quadrati perfetti.

Passo 1: Scomponi il numero in fattori primi. Un fattore primo è un numero divisibile solo per 1 e per se stesso (es: 2, 3, 5, 7, 11...).

Passo 2: Raggruppa i fattori primi in coppie identiche.

Passo 3: Per ogni coppia, prendi un solo fattore. Moltiplica questi fattori tra loro.

Esempio: Calcoliamo la radice quadrata di 144.

1. Scomposizione in fattori primi: 144 = 2 x 2 x 2 x 2 x 3 x 3

2. Raggruppamento: (2 x 2) x (2 x 2) x (3 x 3)

3. Prendiamo un fattore da ogni coppia: 2 x 2 x 3 = 12

Quindi, √144 = 12

Esercizio: Calcola la radice quadrata di 225 usando la scomposizione in fattori primi.

3. Stima e Approssimazione:

Questo metodo è utile quando non puoi trovare la radice quadrata esatta di un numero e hai bisogno di una stima approssimativa.

Passo 1: Individua i due quadrati perfetti più vicini al numero di cui vuoi trovare la radice quadrata.

Passo 2: Stima a quale dei due quadrati perfetti il tuo numero è più vicino.

Passo 3: La radice quadrata del tuo numero sarà compresa tra le radici quadrate dei due quadrati perfetti. Stima un valore intermedio basandoti su quanto il tuo numero è vicino a uno o all'altro quadrato perfetto.

Esempio: Calcoliamo una stima della radice quadrata di 50.

1. I quadrati perfetti più vicini a 50 sono 49 (√49 = 7) e 64 (√64 = 8).

2. 50 è molto più vicino a 49 che a 64.

3. Quindi, la radice quadrata di 50 sarà leggermente superiore a 7. Potremmo stimare che sia circa 7.1 o 7.2.

Con una calcolatrice, √50 ≈ 7.07. La nostra stima era piuttosto precisa!

Esercizio: Stima la radice quadrata di 85.

Radici Quadrate nella Vita di Tutti i Giorni

Potresti pensare che le radici quadrate siano qualcosa di astratto che si studia solo a scuola, ma in realtà le utilizziamo (spesso senza accorgercene) in molte situazioni quotidiane:

Architettura e Design: Per calcolare le dimensioni di una stanza quadrata o determinare la lunghezza dei lati di un giardino quadrato.
Fisica: In molte formule che riguardano il movimento, l'energia e le onde.
Informatica: Nello sviluppo di videogiochi e nella grafica 3D.
Navigazione: Per calcolare distanze e percorsi, soprattutto con il teorema di Pitagora (che si basa sulle radici quadrate).

Ad esempio, immagina di voler costruire una recinzione per un giardino quadrato di 16 metri quadrati. Per sapere quanti metri di recinzione ti servono, devi calcolare la radice quadrata di 16, che è 4. Quindi, ogni lato del giardino sarà lungo 4 metri, e ti serviranno 4 x 4 = 16 metri di recinzione.

Consigli e Trucchi per Imparare le Radici Quadrate

Memorizza i quadrati perfetti più comuni: Sapere a memoria i quadrati dei numeri da 1 a 15 (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225) ti aiuterà a riconoscere immediatamente molte radici quadrate.
Usa flashcard: Scrivi un numero su un lato della flashcard e la sua radice quadrata sull'altro. Ripetile regolarmente per memorizzarle.
Pratica, pratica, pratica: Più esercizi fai, più diventerai bravo a calcolare le radici quadrate.
Usa risorse online: Ci sono molti siti web e app che offrono esercizi interattivi e tutorial sulle radici quadrate.
Non aver paura di chiedere aiuto: Se hai difficoltà, chiedi aiuto al tuo insegnante, a un tutor o a un compagno di classe.

Secondo uno studio condotto dall'Università di Stanford, gli studenti che utilizzano tecniche di apprendimento attivo, come la pratica e la discussione con i compagni, ottengono risultati significativamente migliori in matematica rispetto a quelli che si limitano ad ascoltare passivamente le lezioni.

Motivazione e Prossimi Passi

Spero che questo articolo ti abbia aiutato a capire meglio cosa sono le radici quadrate e come calcolarle. Ricorda che la matematica è un processo, non una destinazione. Non scoraggiarti se all'inizio incontri delle difficoltà. Continua a praticare, a sperimentare e a fare domande. Ogni piccolo passo avanti è un successo!

Prossimi passi: