Come Si Calcolano Le Componenti Di Un Vettore
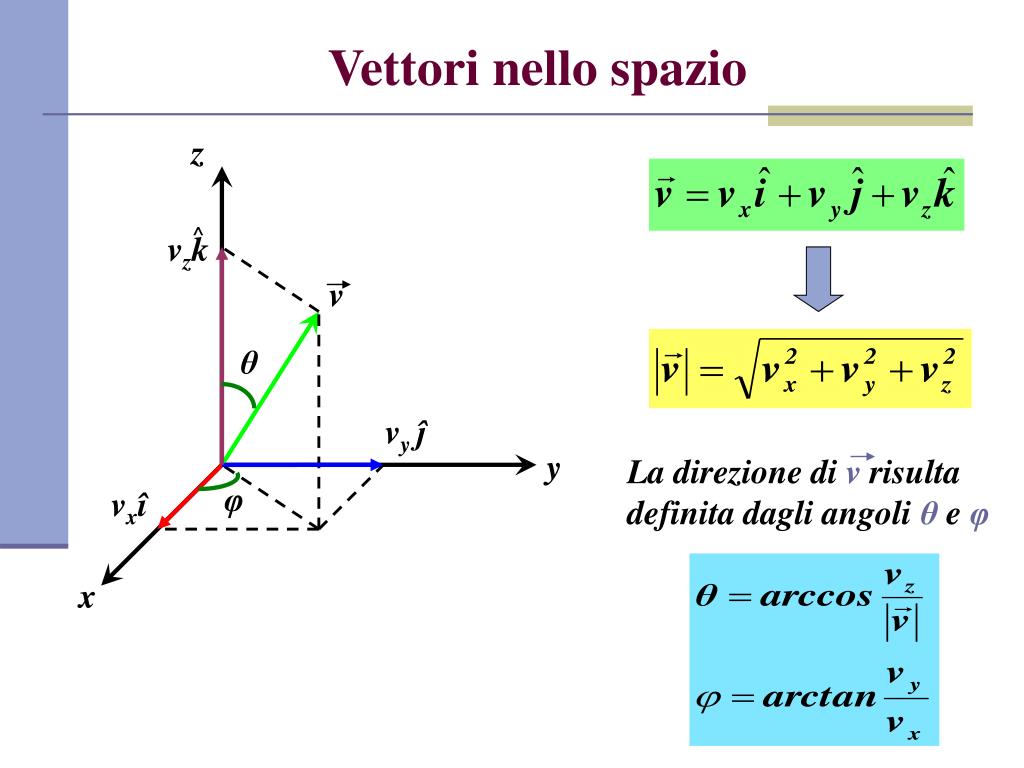
In fisica e matematica, un vettore rappresenta una grandezza caratterizzata da una magnitudine (o modulo), una direzione e un verso. Spesso, per semplificare i calcoli e l'analisi dei fenomeni, è necessario scomporre un vettore nelle sue componenti lungo un sistema di coordinate, solitamente cartesiane (x, y, z).
Cosa sono le Componenti di un Vettore?
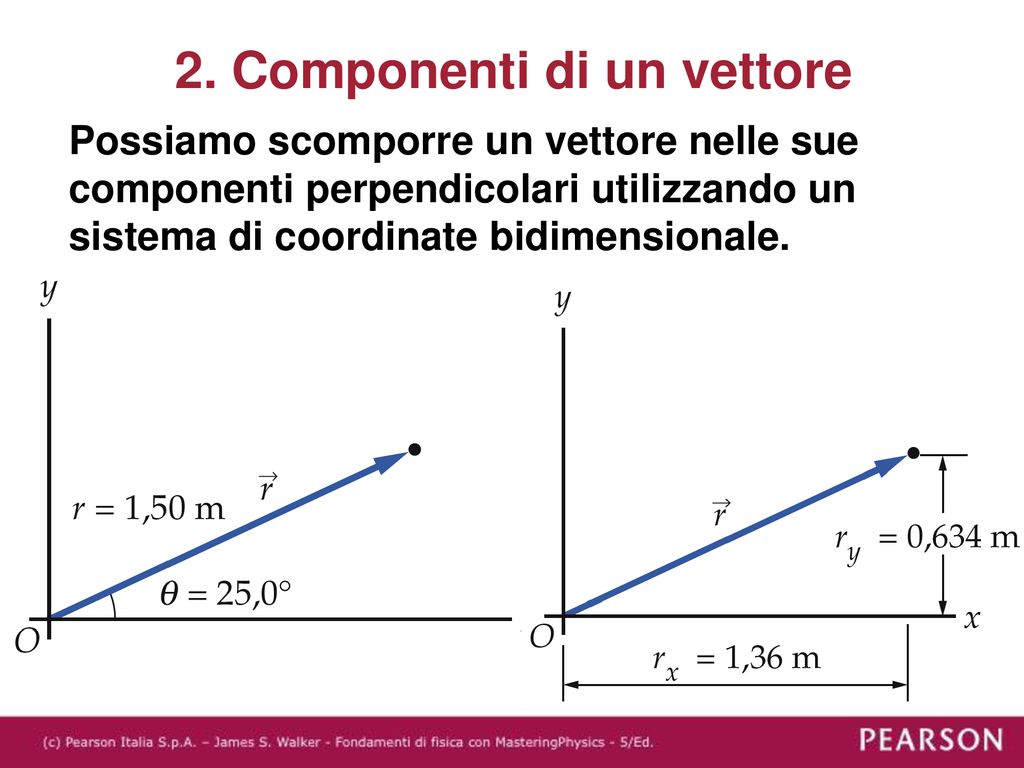
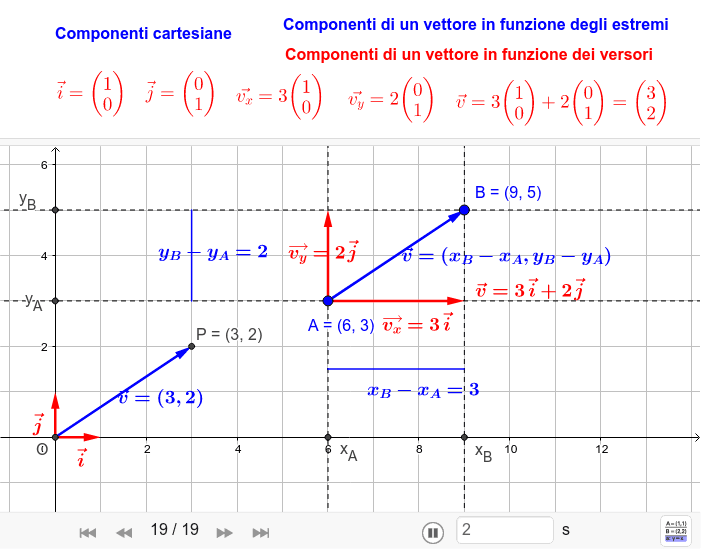
Le componenti di un vettore sono le proiezioni del vettore stesso sugli assi di un sistema di coordinate. In due dimensioni (piano), avremo due componenti: la componente orizzontale (x) e la componente verticale (y). In tre dimensioni, si aggiunge la componente lungo l'asse z. Queste componenti ci forniscono informazioni quantitative su quanto il vettore "si estende" in ciascuna direzione.
Perché è Importante Calcolare le Componenti?
La capacità di calcolare le componenti di un vettore è fondamentale per diverse ragioni:
- Semplificazione dei calcoli: Sommare o sottrarre vettori diventa molto più semplice una volta che sono stati scomposti nelle loro componenti. Invece di manipolare direttamente le grandezze con direzione e verso, si opera semplicemente con numeri (le componenti) lungo ciascun asse.
- Analisi dei movimenti: In fisica, lo studio del moto (cinematica) spesso richiede la scomposizione delle forze e delle velocità nelle loro componenti per analizzare separatamente il movimento orizzontale e verticale.
- Risoluzione di problemi complessi: Molti problemi di fisica, come quelli riguardanti la meccanica o l'elettromagnetismo, richiedono l'uso di componenti vettoriali per essere risolti in modo efficiente.
Come afferma Resnick, Halliday e Krane nel loro celebre testo di fisica, "La scomposizione di un vettore nelle sue componenti è una tecnica essenziale per l'analisi e la risoluzione di problemi in fisica."
Come si Calcolano le Componenti?
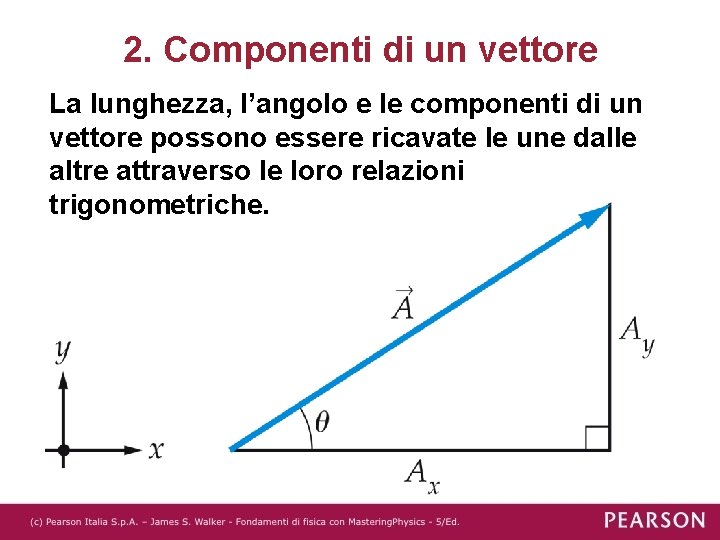
Il calcolo delle componenti di un vettore si basa principalmente sulla trigonometria. Se conosciamo il modulo (A) del vettore e l'angolo (θ) che forma con l'asse x, possiamo calcolare le componenti Ax e Ay come segue:
Ax = A * cos(θ)
Ay = A * sin(θ)
Dove:
- Ax è la componente del vettore lungo l'asse x.
- Ay è la componente del vettore lungo l'asse y.
- A è il modulo (lunghezza) del vettore.
- θ è l'angolo tra il vettore e l'asse x.
È fondamentale assicurarsi che la calcolatrice sia impostata sulla modalità corretta (gradi o radianti) a seconda dell'unità di misura dell'angolo.
Applicazioni Pratiche per gli Studenti
L'applicazione di questo concetto è vastissima nella vita scolastica e quotidiana:
- Fisica: Calcolo della gittata di un proiettile, analisi delle forze agenti su un oggetto inclinato, studio del moto armonico.
- Matematica: Geometria analitica, trigonometria.
- Vita quotidiana: Immagina di spingere un carrello della spesa. La forza che applichi può essere scomposta in una componente orizzontale, che lo fa muovere in avanti, e una componente verticale, che contribuisce a sostenerlo. Capire queste componenti aiuta a ottimizzare la spinta.
Inoltre, la comprensione delle componenti vettoriali è cruciale per discipline come l'ingegneria, l'architettura e l'informatica grafica.
In conclusione, la padronanza del calcolo delle componenti di un vettore è un'abilità fondamentale per gli studenti di scienze e non solo, aprendo le porte a una comprensione più profonda del mondo che ci circonda.



.jpg)