Come Si Calcola L'area Laterale Di Un Cubo

Il calcolo dell'area laterale di un cubo è un'operazione fondamentale in geometria solida, e la sua comprensione è cruciale per diverse applicazioni pratiche. Questo articolo si propone di spiegare in modo chiaro e dettagliato come calcolare l'area laterale di un cubo, fornendo una guida passo-passo e illustrando il concetto con esempi concreti.

Comprendere il Cubo e le Sue Proprietà

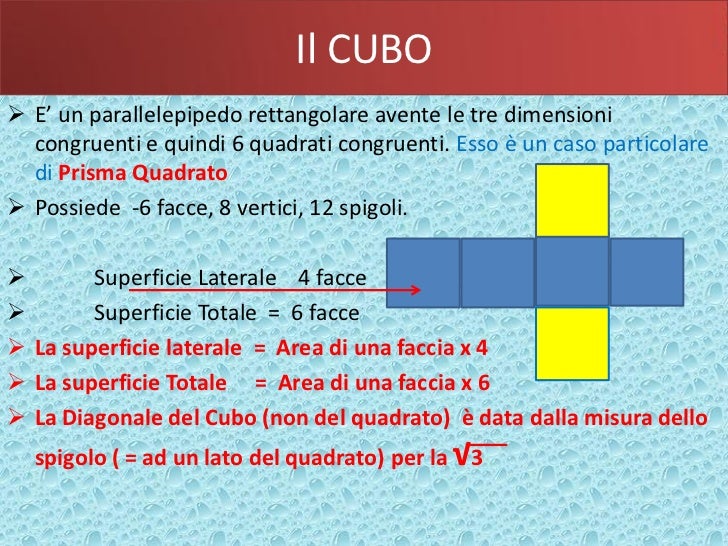
Prima di addentrarci nel calcolo dell'area laterale, è essenziale comprendere le caratteristiche principali di un cubo. Un cubo è un solido geometrico tridimensionale delimitato da sei facce quadrate identiche. Ogni faccia è un quadrato perfetto, il che significa che tutti i lati hanno la stessa lunghezza. Questa lunghezza, solitamente indicata con la lettera 'l', è un parametro cruciale per determinare l'area laterale e totale del cubo.

Un cubo ha 8 vertici, che sono i punti in cui tre facce si incontrano, e 12 spigoli, che sono i segmenti di linea che connettono i vertici. La regolarità e la simmetria del cubo lo rendono una figura geometrica particolarmente semplice da studiare e calcolare.

Definizione di Area Laterale

L'area laterale di un cubo si riferisce alla somma delle aree di tutte le sue facce laterali, escludendo le due basi (la faccia superiore e quella inferiore). In altre parole, è l'area della "superficie esterna" del cubo, senza considerare le facce che fungono da base. Poiché un cubo ha quattro facce laterali, calcolare l'area laterale significa calcolare l'area di una faccia e moltiplicarla per quattro.

Calcolo dell'Area di una Faccia

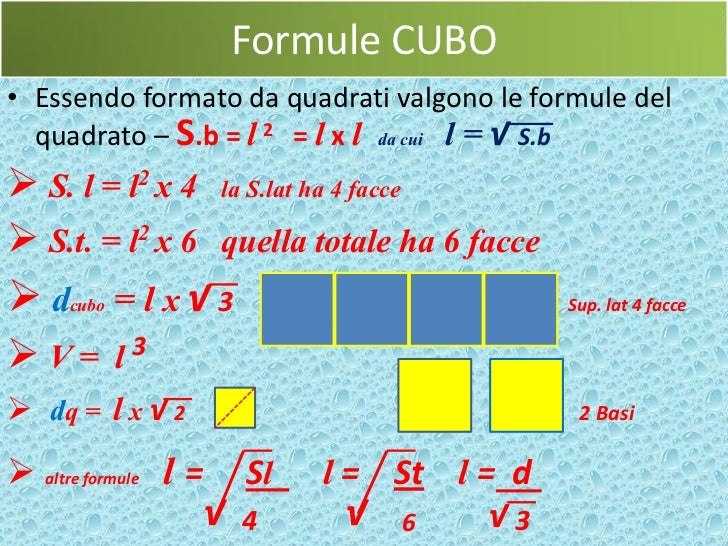
Il primo passo per calcolare l'area laterale di un cubo è determinare l'area di una singola faccia. Come accennato in precedenza, ogni faccia è un quadrato perfetto. L'area di un quadrato si calcola elevando al quadrato la lunghezza del suo lato. Quindi, se 'l' è la lunghezza del lato del cubo, l'area di una faccia (A_f) è data dalla formula:

A_f = l²

Questa formula è fondamentale e rappresenta la base per tutti i calcoli successivi. Assicuriamoci di avere chiara la lunghezza del lato del cubo, espressa nella stessa unità di misura per tutti i calcoli.

Calcolo dell'Area Laterale

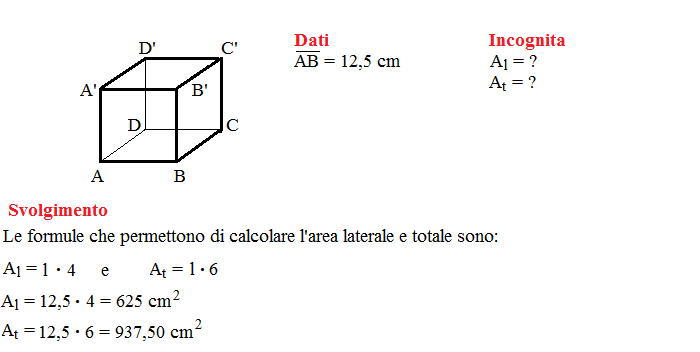
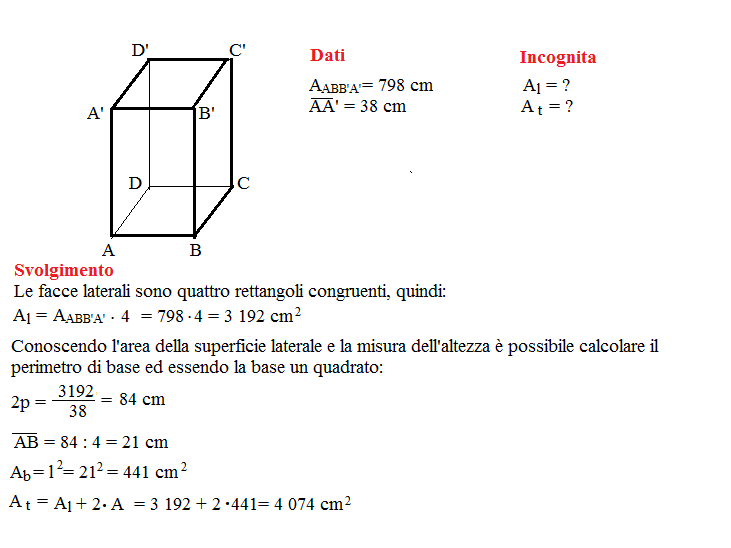
Una volta calcolata l'area di una singola faccia, il calcolo dell'area laterale (A_l) è molto semplice. Dato che un cubo ha quattro facce laterali, l'area laterale è quattro volte l'area di una singola faccia. Pertanto, la formula per calcolare l'area laterale di un cubo è:

A_l = 4 * A_f = 4 * l²

Questa è la formula chiave per calcolare l'area laterale di un cubo. Ricorda che l'unità di misura dell'area laterale sarà il quadrato dell'unità di misura della lunghezza del lato (ad esempio, se 'l' è espresso in centimetri, l'area laterale sarà espressa in centimetri quadrati).

Esempio Pratico

Supponiamo di avere un cubo con un lato di 5 cm. Per calcolare l'area laterale, seguiamo i passaggi indicati:

Calcola l'area di una singola faccia: A_f = l² = 5² = 25 cm²
Calcola l'area laterale: A_l = 4 * A_f = 4 * 25 = 100 cm²

Quindi, l'area laterale del cubo è di 100 cm².

Confronto con l'Area Totale

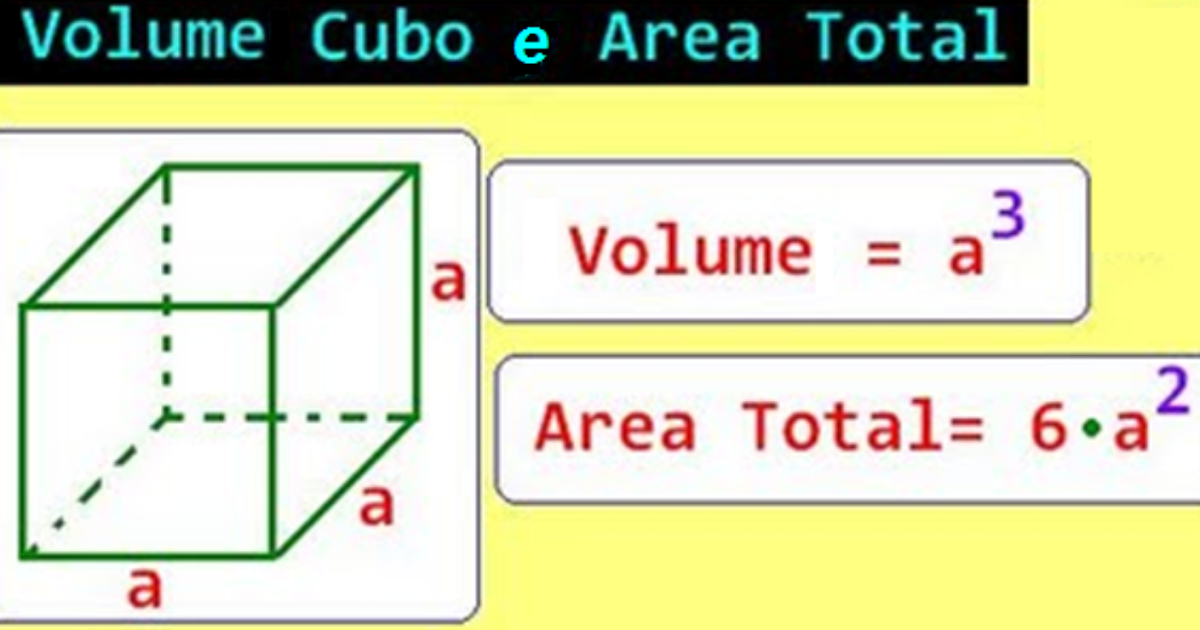
È importante distinguere l'area laterale dall'area totale di un cubo. L'area totale include l'area di tutte e sei le facce, mentre l'area laterale considera solo le quattro facce laterali. La formula per calcolare l'area totale (A_t) di un cubo è:

A_t = 6 * l²

Utilizzando l'esempio precedente, l'area totale del cubo con lato di 5 cm sarebbe: A_t = 6 * 5² = 6 * 25 = 150 cm². Come puoi vedere, l'area totale è significativamente maggiore dell'area laterale.

Applicazioni Pratiche nel Mondo Reale

Il calcolo dell'area laterale di un cubo ha diverse applicazioni pratiche in vari settori. Ecco alcuni esempi:

Imballaggio: Quando si progetta una scatola a forma di cubo, il calcolo dell'area laterale è fondamentale per determinare la quantità di materiale necessaria per la sua costruzione, escludendo la base e il coperchio. Questo aiuta a ottimizzare l'uso delle risorse e ridurre i costi.
Architettura: Nella progettazione di edifici con forme cubiche, conoscere l'area laterale è importante per stimare la quantità di materiale necessario per rivestire le pareti esterne, come mattoni, pannelli o vernice. Ad esempio, un architetto potrebbe dover calcolare l'area laterale di una serie di cubi che compongono un'installazione artistica.
Ingegneria: In ingegneria, il calcolo dell'area laterale può essere utilizzato per determinare la superficie di scambio termico di un componente a forma di cubo, come un dissipatore di calore. Questo è particolarmente importante per garantire un'efficiente dissipazione del calore e prevenire il surriscaldamento.
Calcolo del consumo di vernice: Se si deve verniciare un oggetto a forma di cubo (esclusa la base), il calcolo dell'area laterale permette di stimare la quantità di vernice necessaria. Ad esempio, un artista che realizza sculture cubiche ha bisogno di calcolare la superficie da dipingere per stimare quanto colore gli occorre.
Giochi e Modellismo: Nel modellismo e nella creazione di giochi da tavolo, il calcolo dell'area laterale è utile per determinare la quantità di materiale necessario per costruire dadi o altri elementi cubici.

Questi sono solo alcuni esempi, ma dimostrano come la comprensione del calcolo dell'area laterale di un cubo possa essere utile in diverse situazioni pratiche.

Errori Comuni da Evitare

Durante il calcolo dell'area laterale di un cubo, è importante evitare alcuni errori comuni:

Confondere l'area laterale con l'area totale: Ricorda che l'area laterale include solo quattro facce, mentre l'area totale ne include sei.
Utilizzare unità di misura incoerenti: Assicurati che la lunghezza del lato sia espressa nella stessa unità di misura che utilizzi per calcolare l'area.
Dimenticare di elevare al quadrato la lunghezza del lato: L'area di una singola faccia è data da l², non semplicemente da l.
Non moltiplicare per 4 l'area di una singola faccia: Ricorda che l'area laterale è la somma delle aree di quattro facce.

Prestando attenzione a questi errori, puoi assicurarti di ottenere risultati accurati.

Conclusione

In conclusione, il calcolo dell'area laterale di un cubo è un'operazione semplice ma fondamentale in geometria solida. Comprendere le proprietà del cubo e applicare correttamente la formula A_l = 4 * l² ti permetterà di risolvere problemi pratici in diversi contesti. Speriamo che questa guida ti sia stata utile per chiarire il concetto e fornirti gli strumenti necessari per calcolare l'area laterale di un cubo con sicurezza e precisione.

Esercitati! Prendi un oggetto a forma di cubo che hai a portata di mano, misura la lunghezza del suo lato e calcola la sua area laterale. Questo ti aiuterà a consolidare la tua comprensione del concetto e a sviluppare le tue abilità di calcolo.