Come Si Calcola L'area Del Triangolo Equilatero

Capita a tutti, tranquillo! La geometria può sembrare ostica, soprattutto quando ci troviamo di fronte a figure come il triangolo equilatero. Forse ti sei bloccato a scuola, forse stai ripassando per un esame, o magari sei semplicemente curioso. Qualunque sia il motivo, sei nel posto giusto. Cercheremo di rendere il calcolo dell'area di un triangolo equilatero il più semplice e indolore possibile.

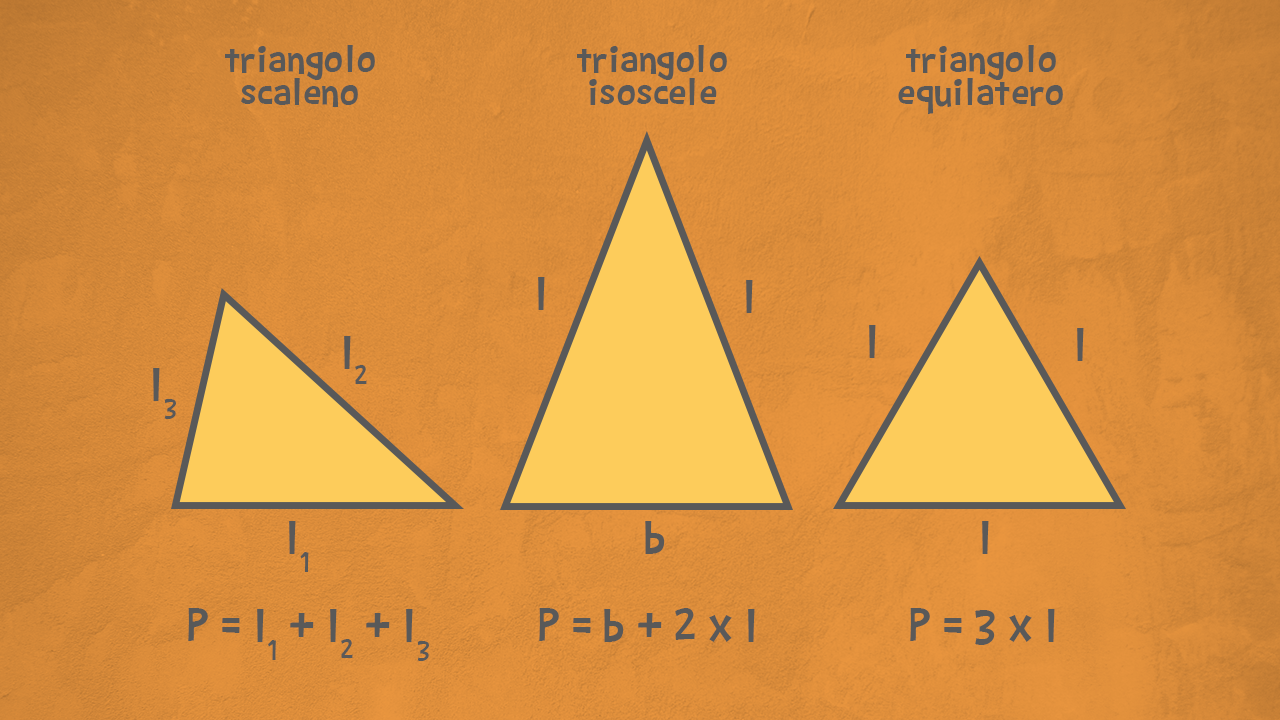
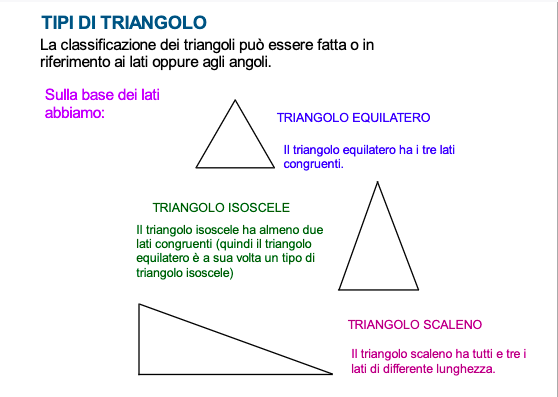
Cos'è un Triangolo Equilatero?

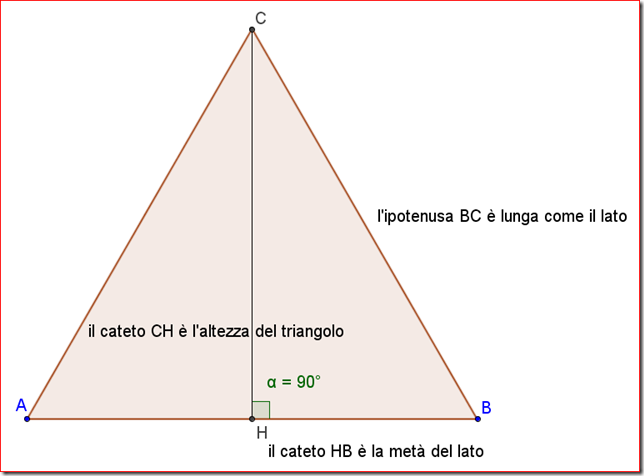
Prima di addentrarci nei calcoli, ricapitoliamo. Un triangolo equilatero è un triangolo speciale. Ha tutti e tre i lati uguali e, di conseguenza, tutti e tre gli angoli uguali (ognuno misura 60 gradi). Questa particolarità lo rende un po' più facile da gestire rispetto ad altri tipi di triangoli.

La Formula Magica (e Come Usarla)

Esiste una formula specifica per calcolare l'area di un triangolo equilatero. È questa:

Area = (lato² * √3) / 4

Dove "lato" rappresenta la lunghezza di uno dei lati del triangolo (ricorda, sono tutti uguali!). La parte "√3" significa "radice quadrata di 3", che è un numero irrazionale approssimativamente uguale a 1.732. Non spaventarti! La calcolatrice è tua amica.

Esempio Pratico

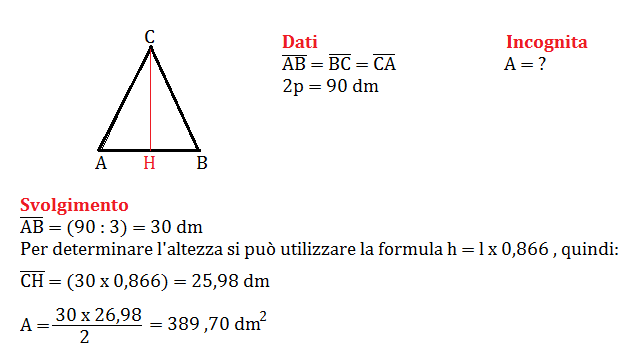
Supponiamo di avere un triangolo equilatero con un lato di 6 cm. Applichiamo la formula:

1. Lato²: 6 cm * 6 cm = 36 cm²
2. Moltiplichiamo per √3: 36 cm² * 1.732 (circa) = 62.352 cm² (circa)
3. Dividiamo per 4: 62.352 cm² / 4 = 15.588 cm² (circa)

Quindi, l'area del nostro triangolo equilatero è di circa 15.588 cm².

Alternative e Trucchi

Se per qualche motivo non ricordi la formula specifica, c'è un altro modo per calcolare l'area, anche se un po' più lungo. Puoi usare la formula generale per l'area di un triangolo qualsiasi:

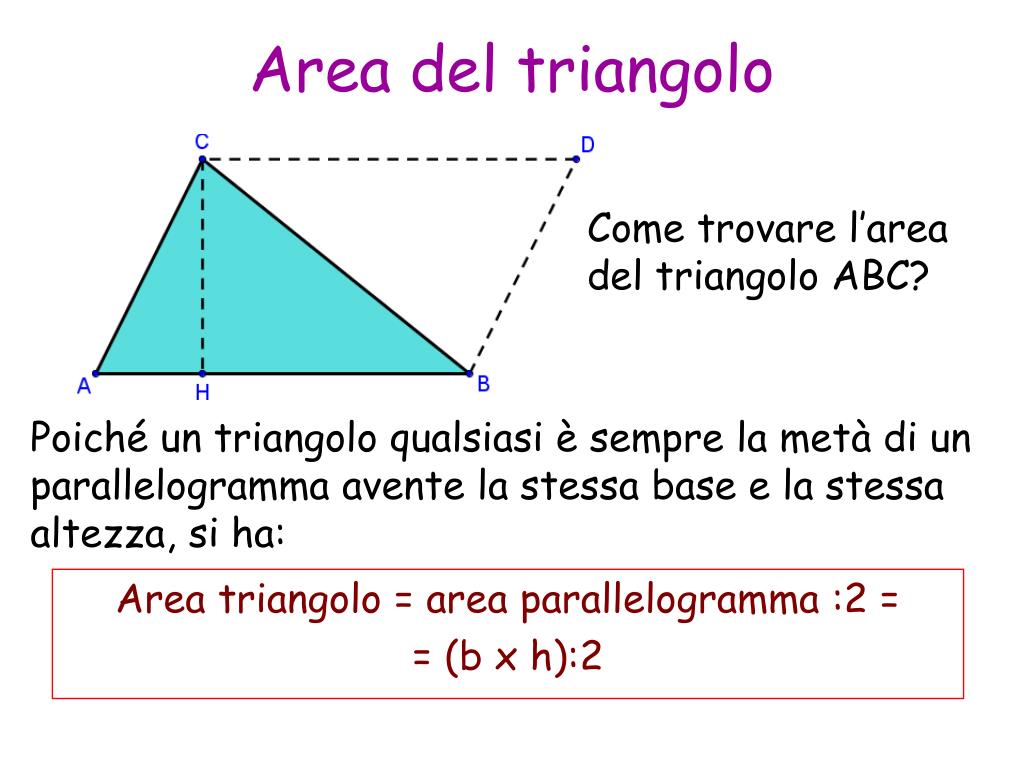
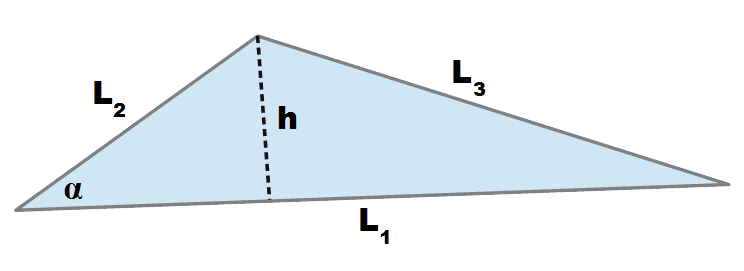
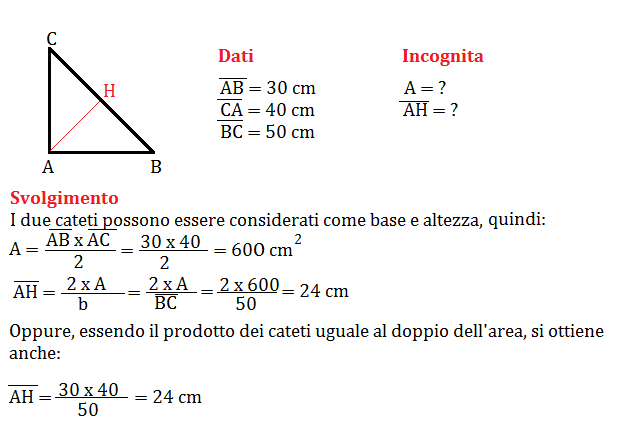
Area = (base * altezza) / 2

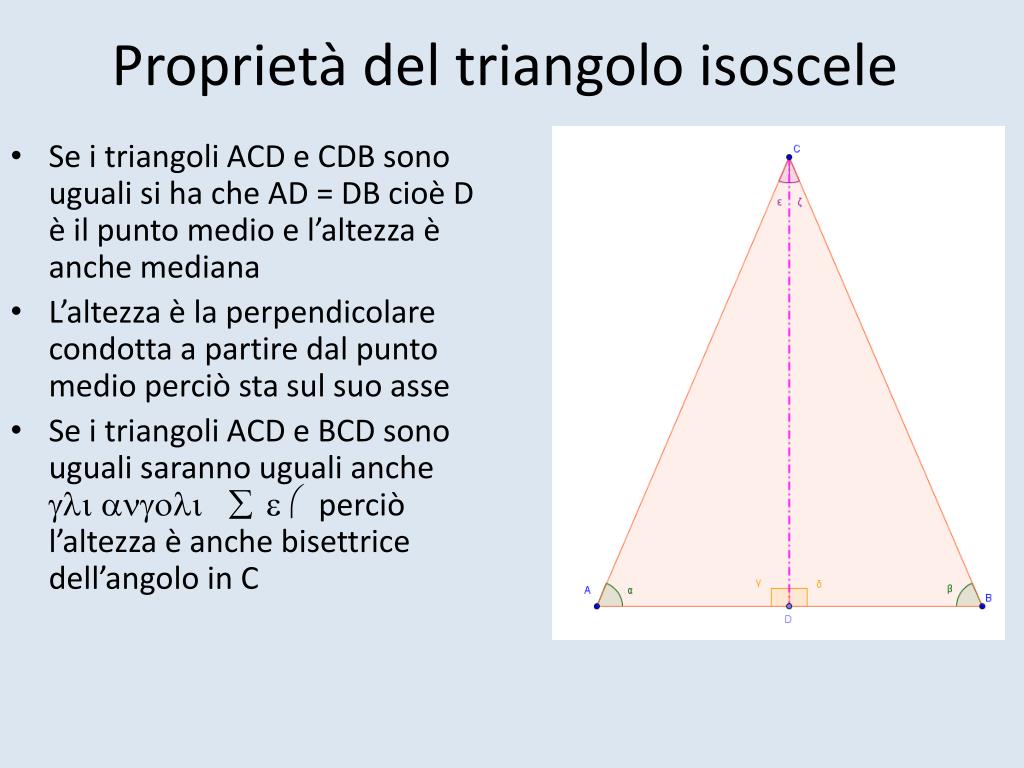
In questo caso, la base è semplicemente uno dei lati del triangolo. L'altezza, invece, è la distanza perpendicolare dalla base al vertice opposto. Per trovare l'altezza di un triangolo equilatero, puoi usare il teorema di Pitagora, dato che l'altezza divide il triangolo equilatero in due triangoli rettangoli congruenti. Ma, come vedi, la formula specifica per il triangolo equilatero è decisamente più veloce!

Un Consiglio Extra

Quando ti trovi di fronte a un problema di geometria, disegna sempre la figura! Visualizzare il triangolo equilatero ti aiuterà a capire meglio il problema e ad applicare la formula correttamente. Inoltre, non aver paura di usare la calcolatrice. La matematica non è una gara di memoria, ma una questione di comprensione e applicazione di concetti.

Non Mollare!

La geometria può sembrare difficile all'inizio, ma con la pratica diventerà sempre più facile. Ricorda che l'importante è capire il concetto e saper applicare la formula. Non scoraggiarti se non riesci subito. Rileggi, fai altri esercizi, e chiedi aiuto se ne hai bisogno. Sei capace di farcela!

Spero che questa spiegazione ti sia stata utile. Ora, vai e conquista quei triangoli equilateri!