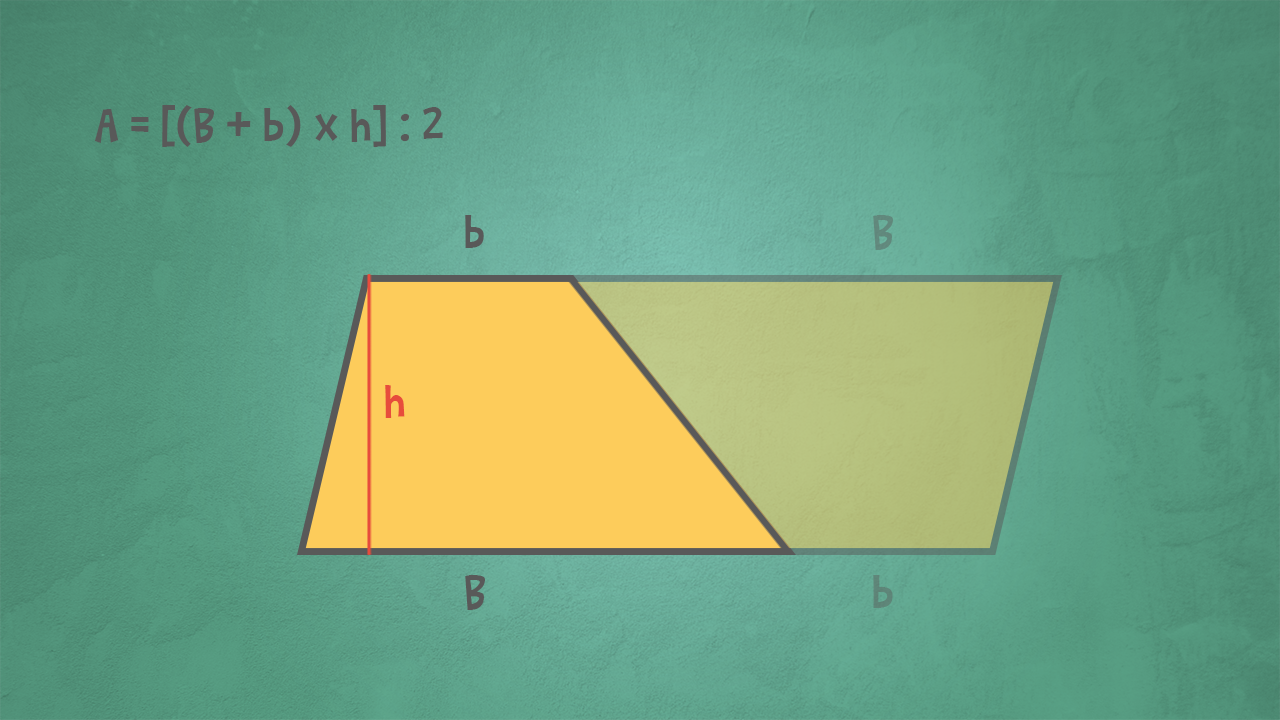Come Si Calcola L'area Del Trapezio Scaleno

Quante volte vi siete trovati di fronte a un trapezio scaleno, magari in un problema di geometria o durante la preparazione per un esame, sentendo un nodo stringervi lo stomaco? Tranquilli, non siete soli. Molti studenti, genitori che cercano di aiutare i figli con i compiti e persino alcuni insegnanti si trovano a dover rispolverare le proprie conoscenze quando si tratta di calcolare l'area di questa figura geometrica apparentemente complessa. La buona notizia è che, con la giusta guida, il calcolo dell'area del trapezio scaleno diventa un gioco da ragazzi. Dimenticate la frustrazione: siamo qui per rendere questo processo chiaro, semplice e persino divertente!

Cos'è un Trapezio Scaleno?

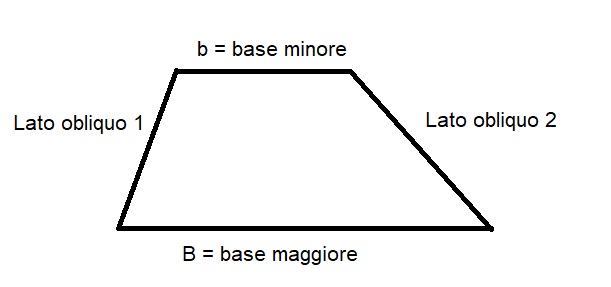
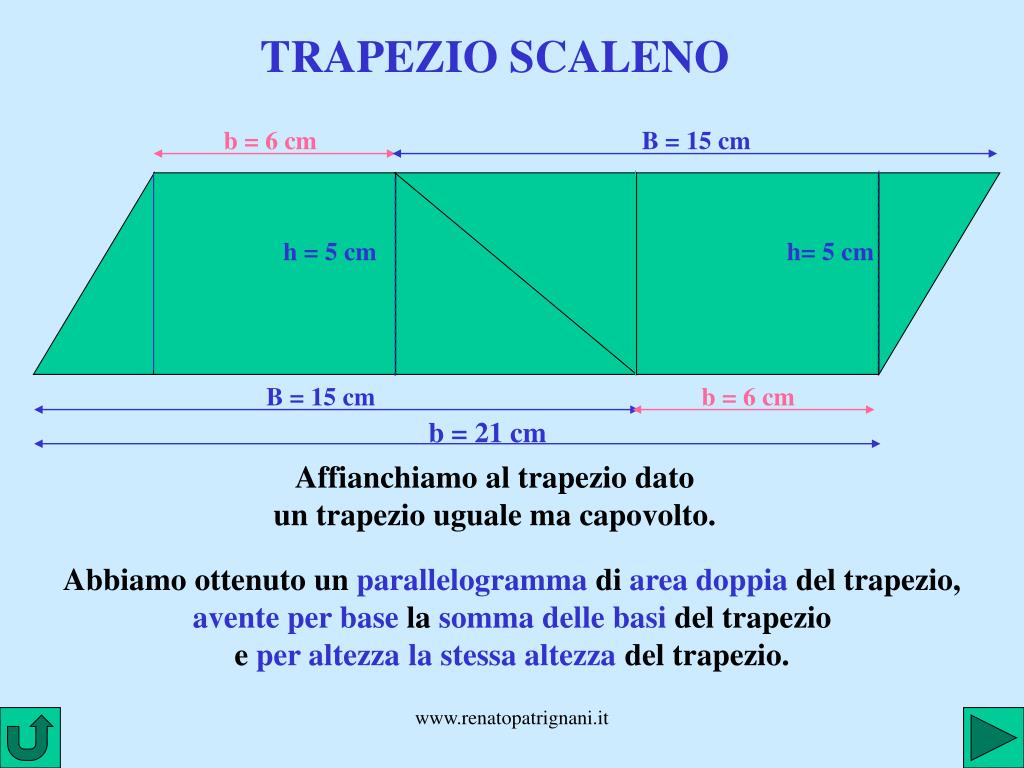
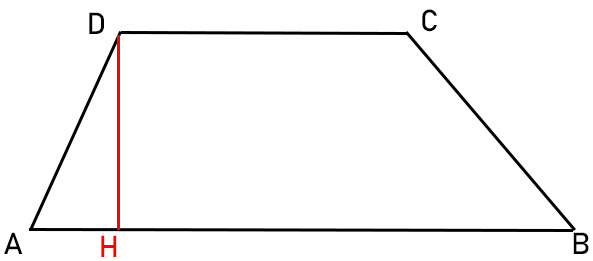
Prima di addentrarci nei calcoli, facciamo un breve ripasso. Un trapezio è un quadrilatero con almeno due lati paralleli, chiamati basi. Nel trapezio scaleno, i due lati non paralleli (gli obliqui) sono di lunghezza diversa. Questa caratteristica lo distingue dal trapezio isoscele (con lati obliqui uguali) e dal trapezio rettangolo (con un lato perpendicolare alle basi).

Riconoscere un trapezio scaleno è fondamentale. Prestate attenzione alle lunghezze dei lati e agli angoli. Se vedete un quadrilatero con due lati paralleli e gli altri due di lunghezza differente, ecco a voi un trapezio scaleno! Questa figura geometrica si presenta spesso in contesti reali, come nella forma di un tetto, di un pezzo di terreno o di un elemento di design.

Metodi per Calcolare l'Area di un Trapezio Scaleno

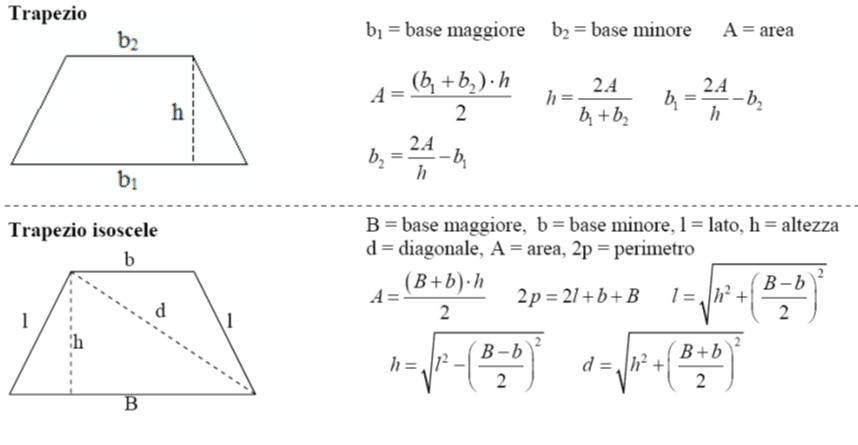
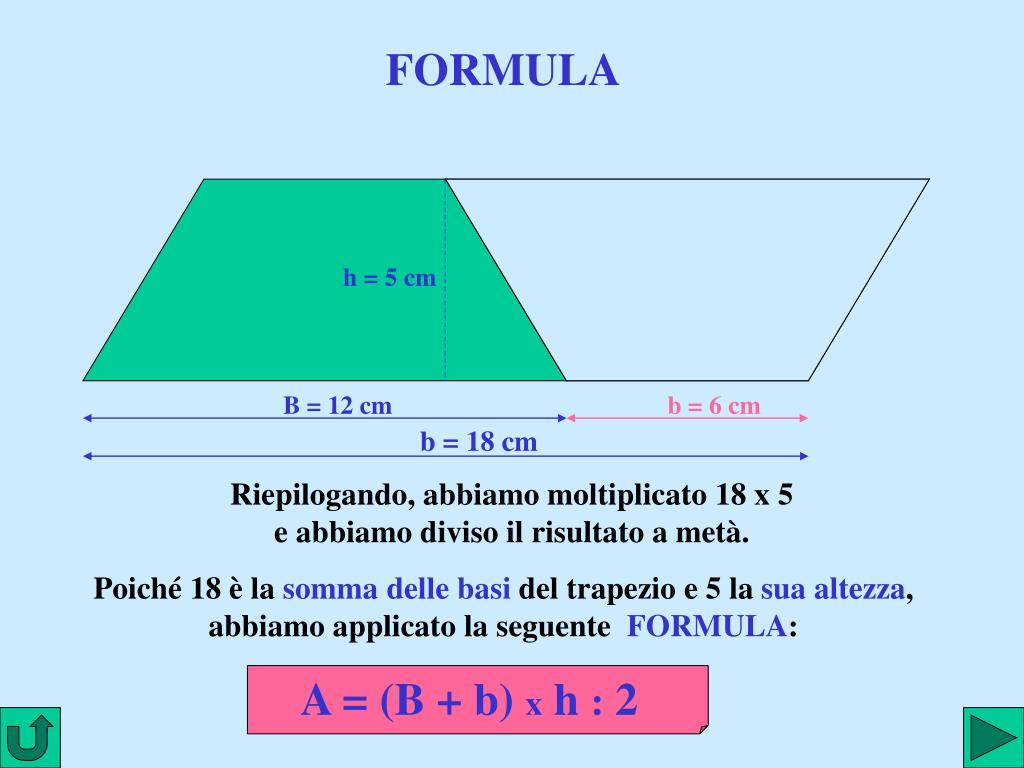
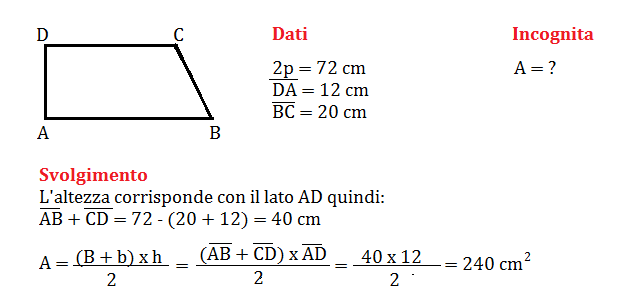
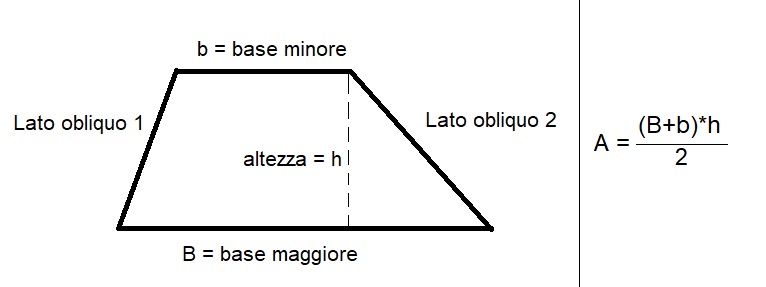
Esistono diversi modi per calcolare l'area di un trapezio scaleno. Il metodo più comune e diretto si basa sulla seguente formula:

Area = (Base Maggiore + Base Minore) * Altezza / 2

Dove:

* Base Maggiore è la lunghezza del lato parallelo più lungo. * Base Minore è la lunghezza del lato parallelo più corto. * Altezza è la distanza perpendicolare tra le due basi.

Esempio Pratico:

Immaginate un trapezio scaleno con una base maggiore di 10 cm, una base minore di 6 cm e un'altezza di 4 cm. L'area si calcolerebbe così:

Area = (10 cm + 6 cm) * 4 cm / 2 = 16 cm * 4 cm / 2 = 32 cm²

Quindi, l'area del trapezio è di 32 centimetri quadrati.

Quando non si conosce l'altezza?

A volte, i problemi non forniscono direttamente l'altezza del trapezio. In questi casi, è necessario ricorrere ad altri metodi per calcolarla:

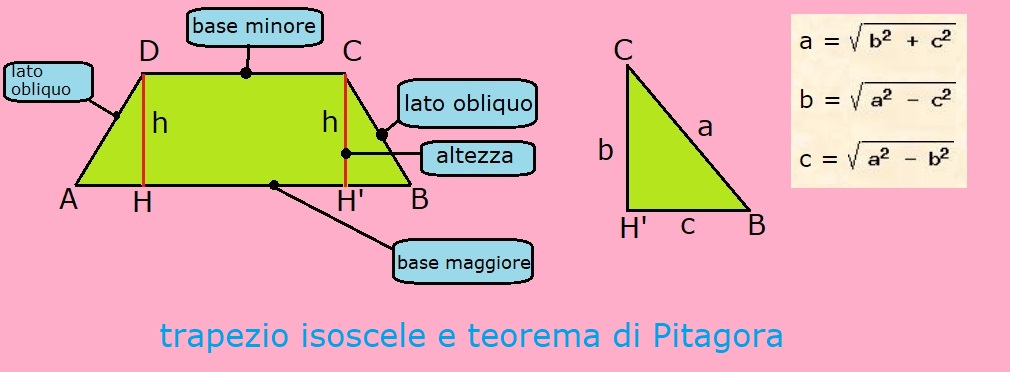
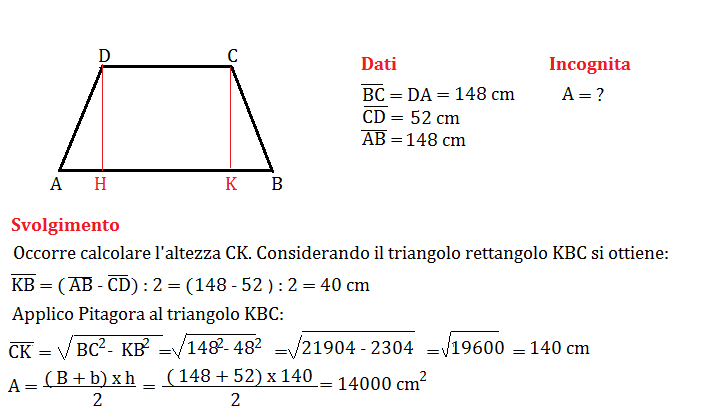
Utilizzo del Teorema di Pitagora: Se si conoscono le lunghezze dei lati obliqui e la differenza tra le proiezioni dei lati obliqui sulla base maggiore, si può formare un triangolo rettangolo e utilizzare il teorema di Pitagora per calcolare l'altezza. Questo richiede un po' di geometria e trigonometria, ma è un metodo efficace.
Trigonometria: Se si conoscono gli angoli formati dai lati obliqui con le basi, si possono utilizzare le funzioni trigonometriche (seno, coseno, tangente) per calcolare l'altezza. Questo metodo è più avanzato e richiede una buona comprensione dei concetti trigonometrici.
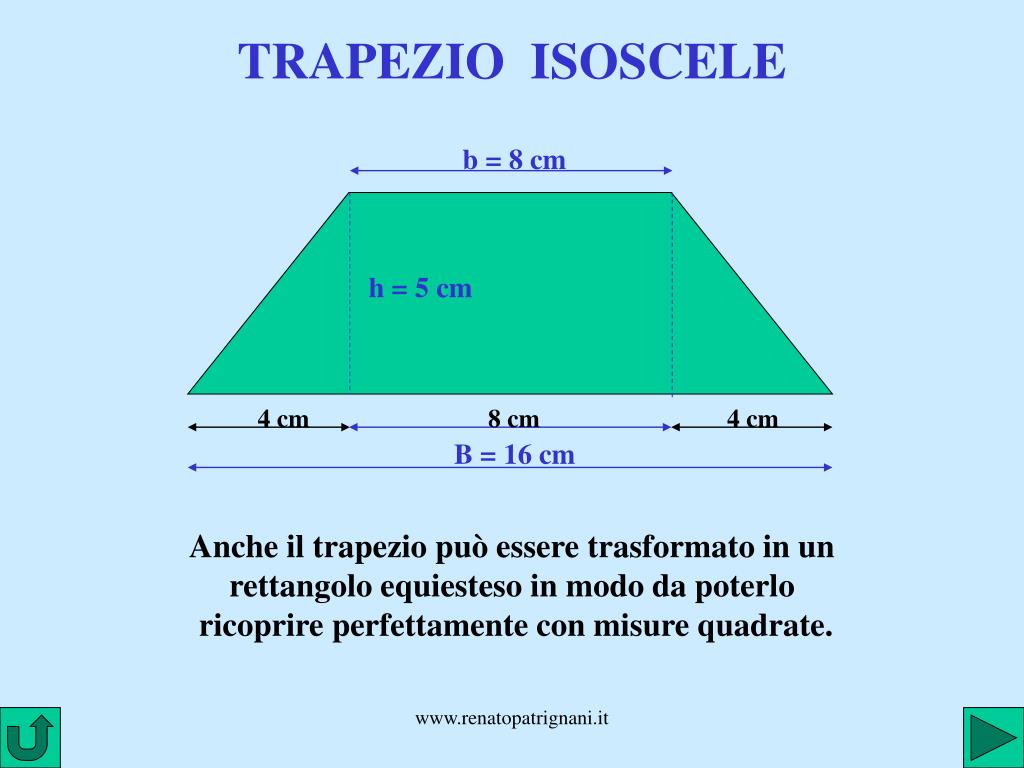
Scomposizione in figure più semplici: Si può dividere il trapezio scaleno in figure più semplici, come rettangoli e triangoli. Calcolare l'area di ciascuna figura e sommare le aree per ottenere l'area totale del trapezio. Questo metodo è particolarmente utile quando si hanno informazioni sufficienti per calcolare le aree delle figure più semplici.

Esempio con il Teorema di Pitagora:

Supponiamo di avere un trapezio scaleno con base maggiore di 12 cm, base minore di 8 cm e un lato obliquo di 5 cm. La proiezione del lato obliquo sulla base maggiore è di 3 cm. Possiamo formare un triangolo rettangolo con il lato obliquo come ipotenusa, la proiezione come cateto e l'altezza come altro cateto. Usando il teorema di Pitagora (a² + b² = c²), abbiamo:

Altezza² = 5² - 3² = 25 - 9 = 16

Altezza = √16 = 4 cm

Ora che conosciamo l'altezza, possiamo calcolare l'area del trapezio usando la formula standard: Area = (12 cm + 8 cm) * 4 cm / 2 = 40 cm²

Consigli Pratici per la Didattica

Per gli insegnanti e i genitori che aiutano i ragazzi con i compiti, ecco alcuni consigli per rendere l'apprendimento più efficace:

* Utilizzare Materiale Concreto: Create trapezi scaleni con cartoncino o altri materiali. Manipolare fisicamente la figura aiuta a visualizzare meglio le basi, l'altezza e l'area. Potete anche utilizzare software di geometria dinamica come GeoGebra per esplorare le proprietà del trapezio scaleno in modo interattivo. * Esempi Reali: Mostrate esempi di trapezi scaleni presenti nella vita reale. Un tetto, un pezzo di terra, un cartello stradale. Collegare la geometria alla realtà rende l'apprendimento più significativo. * Risoluzione di Problemi Guidata: Affrontate i problemi gradualmente, guidando gli studenti passo dopo passo. Iniziate con problemi semplici, fornendo tutte le informazioni necessarie, e poi aumentate gradualmente la difficoltà. * Collaborazione: Incoraggiate gli studenti a lavorare in gruppo, a discutere i problemi e a condividere le proprie soluzioni. L'apprendimento collaborativo favorisce la comprensione e la memorizzazione dei concetti. * Feedback Costruttivo: Fornite feedback specifici e costruttivi, evidenziando i punti di forza e le aree di miglioramento. Concentratevi sul processo di risoluzione dei problemi, piuttosto che solo sul risultato finale.

Errori Comuni da Evitare

Durante il calcolo dell'area del trapezio scaleno, è facile commettere alcuni errori comuni:

* Confondere le Basi con i Lati Obliqui: Assicuratevi di identificare correttamente le basi (i lati paralleli) prima di applicare la formula. * Utilizzare l'Altezza Sbagliata: L'altezza deve essere la distanza perpendicolare tra le due basi. Un errore comune è utilizzare la lunghezza di uno dei lati obliqui come altezza. * Dimenticare di Dividere per Due: Ricordate che la formula include la divisione per due. Non dimenticate questo passaggio fondamentale! * Errori di Calcolo: Prestate attenzione ai calcoli, soprattutto quando si utilizzano numeri decimali o frazioni. Utilizzate una calcolatrice, se necessario, ma verificate sempre i risultati.

Statistiche e Ricerche

Anche se non ci sono statistiche specifiche sulla difficoltà percepita nel calcolo dell'area del trapezio scaleno, studi sull'apprendimento della geometria mostrano che gli studenti spesso faticano con concetti che richiedono l'applicazione di formule e la visualizzazione spaziale. Un sondaggio informale tra insegnanti di matematica di scuola media ha rivelato che il trapezio (in generale) è spesso identificato come uno degli argomenti più problematici per gli studenti, insieme al teorema di Pitagora e alla trigonometria. La chiave per superare queste difficoltà è un approccio pratico, visivo e basato sulla risoluzione di problemi.

Conclusione

Calcolare l'area di un trapezio scaleno può sembrare complicato all'inizio, ma con la formula giusta e un po' di pratica, diventa un compito accessibile a tutti. Ricordatevi di identificare correttamente le basi e l'altezza, e di applicare la formula con attenzione. Se non conoscete l'altezza, utilizzate il teorema di Pitagora, la trigonometria o la scomposizione in figure più semplici. Con i consigli pratici e gli esempi forniti, sarete in grado di affrontare qualsiasi problema che coinvolga il trapezio scaleno con sicurezza e competenza. Quindi, la prossima volta che vi troverete di fronte a un trapezio scaleno, non abbiate paura: sapete esattamente cosa fare!