Come Si Calcola L'area Del Cilindro

Immagina un cilindro. Un oggetto che incontriamo ovunque: una lattina di bibita, un rotolo di carta, persino alcuni alberi maestosi. Ora, pensa di poterlo "aprire", di svelarne la superficie, comprenderne la forma più intima. Questo è ciò che faremo, calcolando la sua area.
Il calcolo dell'area del cilindro non è solo una formula da memorizzare, ma un viaggio nella geometria, un'esplorazione di concetti che si intrecciano e si rafforzano a vicenda. È un invito a guardare il mondo con occhi diversi, a scomporre la complessità in elementi più semplici.
La Decomposizione: Un Atto di Chiarezza
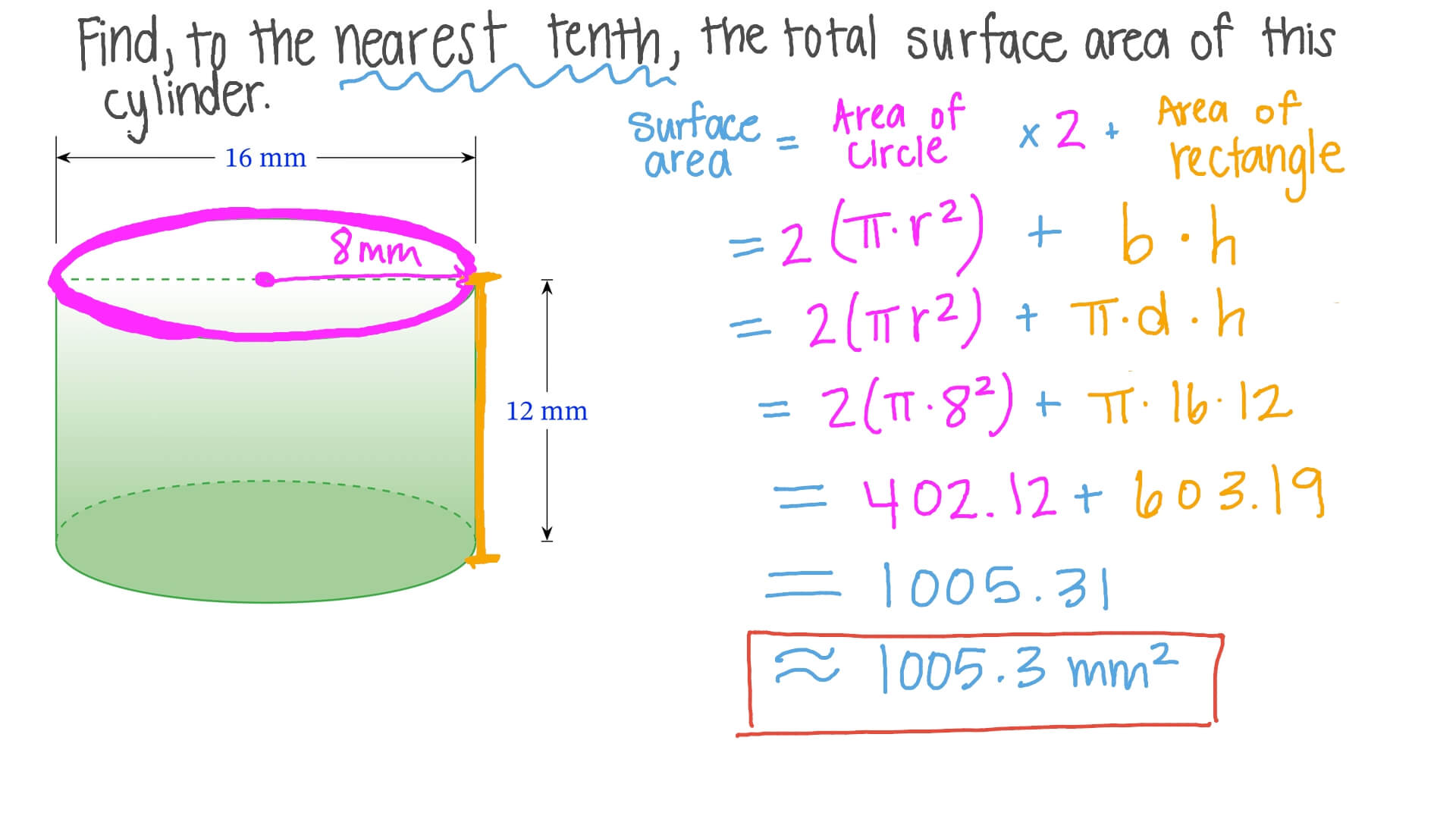
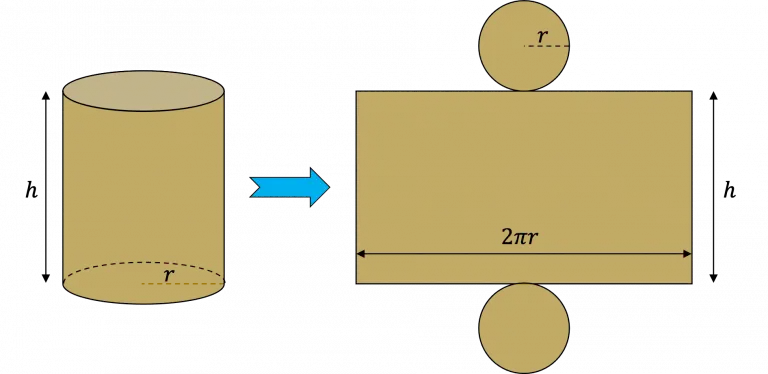
Il segreto per calcolare l'area di un cilindro sta nella sua decomposizione. Possiamo immaginarlo come composto da tre parti fondamentali:
- Due cerchi identici, che formano le basi.
- Un rettangolo, che avvolge la circonferenza dei cerchi.
Quindi, per trovare l'area totale del cilindro, sommiamo l'area di queste tre figure.
Area delle Basi: Il Potere del Cerchio
L'area di un cerchio è un concetto fondamentale, un pilastro della geometria. La formula, che forse già conosci, è: πr², dove π (pi greco) è una costante affascinante e r è il raggio del cerchio. Quindi, l'area totale delle due basi del cilindro sarà 2πr².
"La geometria è l'arte di ragionare correttamente su figure erronee." - Henri Poincaré
Area Laterale: Svelando il Rettangolo Nascosto
L'area laterale del cilindro, quella che avvolge le basi, si rivela essere un rettangolo. La sua altezza corrisponde all'altezza del cilindro (h), e la sua base corrisponde alla circonferenza del cerchio (2πr). Pertanto, l'area laterale è data da 2πrh.
La Formula Finale: Un Inno alla Sintesi
Ora che abbiamo calcolato l'area delle basi e l'area laterale, possiamo sommarle per ottenere l'area totale del cilindro:
Area Totale = Area Laterale + 2 * Area Base = 2πrh + 2πr² = 2πr(h + r)
Questa formula, apparentemente semplice, racchiude in sé tutto il processo di decomposizione e ricomposizione che abbiamo seguito. È un simbolo della nostra capacità di comprendere e dominare il mondo che ci circonda.
Un consiglio: Non limitarti a memorizzare la formula. Cerca di comprenderne il significato, di visualizzare il processo nella tua mente. Questo ti aiuterà a ricordarla più facilmente e a applicarla in contesti diversi.
Oltre il Calcolo: Coltivare la Curiosità
Il calcolo dell'area del cilindro è molto più di un semplice esercizio matematico. È un invito a sviluppare la tua curiosità, a non accontentarti della superficie delle cose, ma a volerle esplorare in profondità. È un invito a perseverare di fronte alle difficoltà, a non arrenderti al primo ostacolo.
Ricorda che l'apprendimento è un processo continuo, un viaggio che dura tutta la vita. Sii umile, riconosci i tuoi limiti, ma non aver paura di sperimentare, di fare errori, di imparare dai tuoi sbagli.
Studiare la geometria, e la matematica in generale, ti offre gli strumenti per comprendere il mondo, per risolvere problemi complessi, per prendere decisioni informate. Ma soprattutto, ti offre l'opportunità di crescere come persona, di sviluppare il tuo pensiero critico, la tua creatività, la tua capacità di innovare.
Abbraccia l'Esplorazione Continua
Quindi, la prossima volta che vedi un cilindro, non limitarti a vederlo come un semplice oggetto. Pensa al processo che abbiamo seguito per calcolarne l'area, alla decomposizione, alla ricomposizione, alla formula finale. E ricorda che, al di là del calcolo, c'è un invito a coltivare la tua curiosità, la tua umiltà e la tua perseveranza.
Il mondo è pieno di meraviglie da scoprire. La matematica è uno degli strumenti più potenti che hai a disposizione per svelarle.