Come Si Calcola L'ampiezza Di Un Angolo Senza Goniometro

Ciao a tutti, giovani esploratori della matematica! Oggi partiamo per un'avventura davvero speciale: imparare a capire gli angoli, a sentirli quasi, senza dover sempre ricorrere al goniometro. Sembra una magia, vero? Ma è una magia che tutti possiamo imparare, un po' come un superpotere che si sblocca con la pratica e la pazienza.
Innanzitutto, voglio dirvi una cosa importantissima: non abbiate paura di sbagliare. La matematica, come la vita, è piena di tentativi. Ogni errore è una lezione, un passo avanti verso la comprensione. Ricordatevi che anche i più grandi matematici hanno commesso errori, l'importante è imparare da essi e non arrendersi mai! Pensate a Pitagora, a Euclide, a tutti coloro che hanno costruito le basi della geometria: anche loro hanno iniziato da zero.
Ma perché è così importante saper calcolare l'ampiezza di un angolo senza goniometro? Beh, immaginate di essere degli architetti che progettano un edificio, degli ingegneri che costruiscono un ponte, o persino degli artisti che creano un'opera d'arte. Gli angoli sono ovunque! Comprendere come funzionano ci permette di costruire, creare e risolvere problemi in modo più efficace e creativo.
Le basi: angoli speciali e relazioni
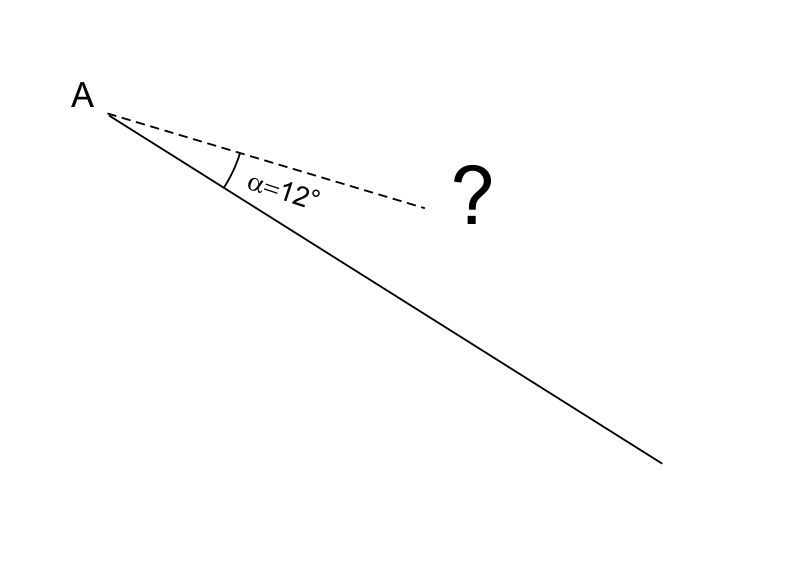
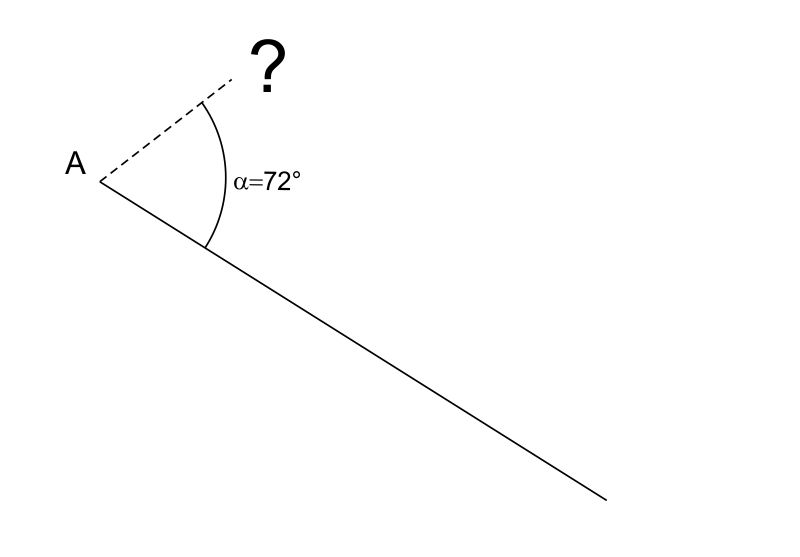
Partiamo dalle basi. Conoscete già gli angoli speciali, vero? L'angolo retto, quello che forma un perfetto angolo di 90 gradi, come l'angolo di un quaderno. L'angolo piatto, che è dritto come un righello, misura 180 gradi. E l'angolo giro, un cerchio completo, che fa 360 gradi. Questi sono i nostri punti di riferimento, le nostre bussole nel mondo degli angoli.
Angoli complementari e supplementari
Ora, scopriamo un segreto: gli angoli amano stare in compagnia! Quando due angoli sommano 90 gradi, si chiamano complementari. Immaginate due amici che si completano a vicenda, come un puzzle che si incastra perfettamente. E quando due angoli sommano 180 gradi, si chiamano supplementari. Pensate a due persone che, insieme, formano un'unica entità, un'unica linea retta.
Se conosci l'ampiezza di un angolo, puoi facilmente calcolare l'ampiezza del suo angolo complementare o supplementare! Basta sottrarre l'angolo conosciuto da 90 o 180 gradi, rispettivamente.
Un esempio? Se un angolo misura 30 gradi, il suo angolo complementare misurerà 90 - 30 = 60 gradi. E il suo angolo supplementare misurerà 180 - 30 = 150 gradi. Facile, no?
Trigonometria: un aiuto inaspettato
Forse avete già sentito parlare della trigonometria. Non spaventatevi! Anche se sembra complicata, è in realtà uno strumento molto potente per capire gli angoli. Le funzioni seno, coseno e tangente ci permettono di collegare gli angoli ai lati dei triangoli rettangoli. Se conoscete la lunghezza di due lati di un triangolo rettangolo, potete usare queste funzioni per calcolare l'ampiezza degli angoli.
Non vi chiedo di diventare esperti di trigonometria dall'oggi al domani. Ma sapere che esiste questo strumento e che può esservi utile è già un grande passo avanti. Ricordatevi che la conoscenza è come un tesoro: più ne accumulate, più ricchi diventate!
L'importanza della pratica e dell'osservazione
La cosa più importante, però, è la pratica. Esercitatevi a riconoscere gli angoli negli oggetti che vi circondano: l'angolo di un tavolo, l'angolo di una finestra, l'angolo formato dalle lancette di un orologio. Più osserverete, più svilupperete il vostro "occhio" per gli angoli. Esercitatevi con esercizi, problemi e sfide. Chiedete aiuto ai vostri insegnanti, ai vostri compagni, ai vostri genitori. Non abbiate paura di chiedere!
Ricordatevi sempre che l'apprendimento è un viaggio, non una destinazione. Godetevi il percorso, siate curiosi, sperimentate, fate domande. E soprattutto, credete in voi stessi. Siete capaci di grandi cose! La matematica, come la vita, è una sfida continua, ma è anche una fonte inesauribile di soddisfazioni. Quindi, prendete in mano la vostra geometria, impugnate la vostra matita e partite all'esplorazione del meraviglioso mondo degli angoli!